Справочные материалы Ряды Маклорена основных элементарных функций и некоторые другие разложения в ряды

1. Бином с произвольным показателем

2. Стандартная экспонента и натуральный логарифм

3. Тригонометрические, обратные тригонометрические и гиперболические функции

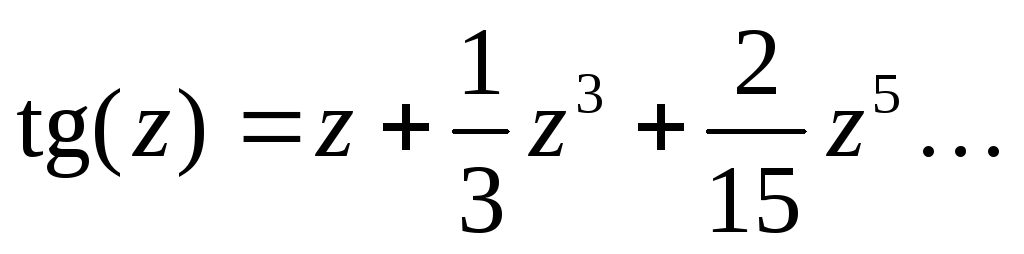
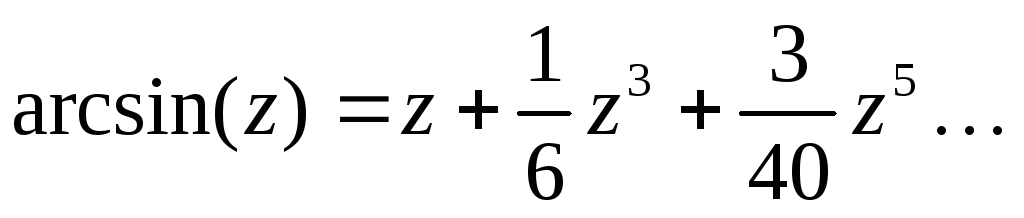
4. Разложение арктангенса при больших значениях переменной ;

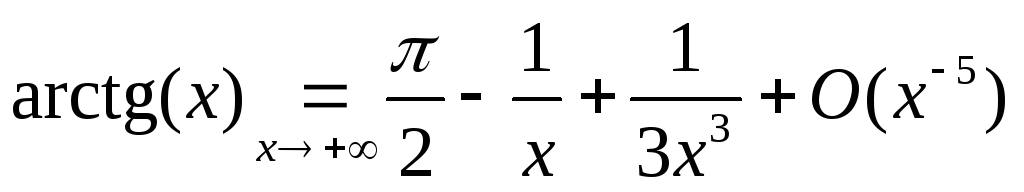Занятие 14. Полное исследование функции и построение графика функции

1. Провести полное исследование и построить графики функций (область определения, четность, нули функции, точки разрыва, вертикальные асимптоты, поведение при больших значениях аргумента – наклонные и горизонтальные асимптоты, локальные экстремумы, точки перегиба):

Занятие 15. Определители: вычисление, свойства. Матрицы: сложение, умножение.

1. Вычислите определители, используя различные способы и принимая во внимание свойства определителей:

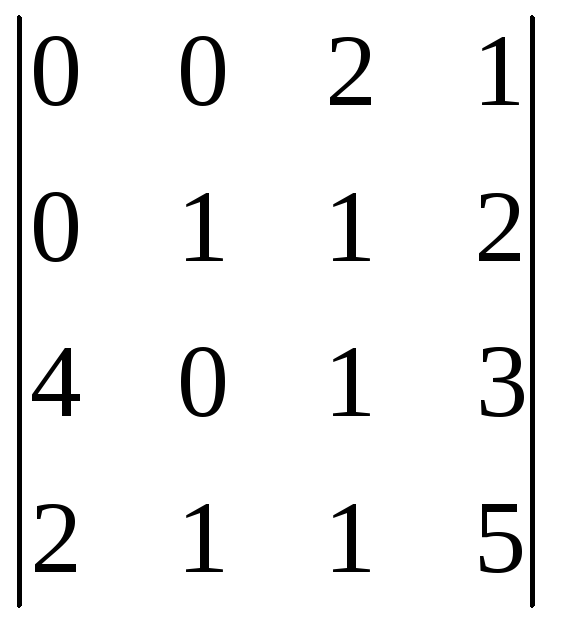1), 2) , 3), 4) , 5)

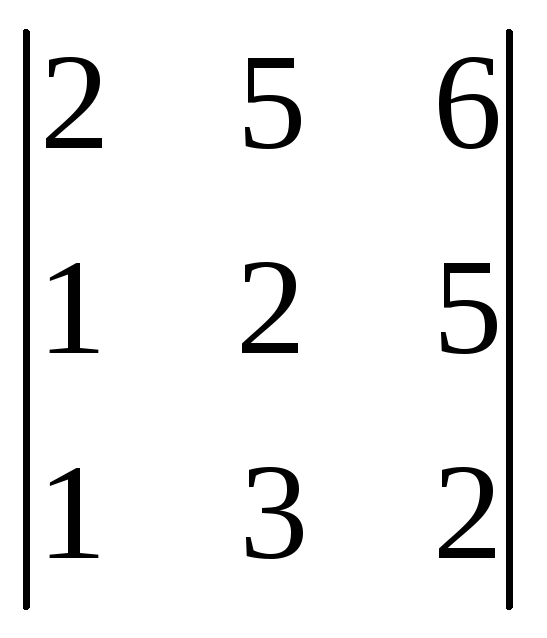
Ответы:10, -14, -1, -14, -1

Контрольные вопросы

1. Как изменится значение второго определителя, если поменять местами первую и вторую строки?

2. Чему равно алгебраическое дополнение элемента -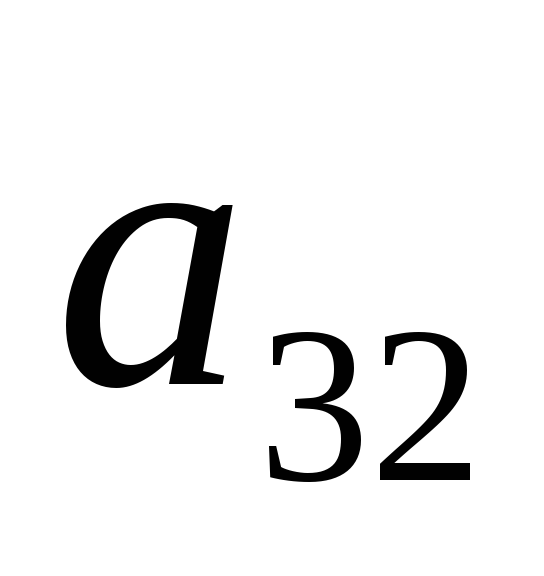-для второго определителя и

четвертого определителя?

3. Найдите значение пятого определителя путем разложения по третьей строке

4. Чему равен определитель, если каждый элемент третьей строки равен соответствующему элементу пятой строки, умноженному на (-3)?

5. Как изменится значение четвертого определителя ,если каждый элемент третьего столбца умножить на число 4?

2. Матрицы. Действия над матрицами. Решение матричных уравнений.

1) Над матрицами и выполнить действия

2) Какими характеристиками должны обладать матрицы, чтобы их можно было перемножить? Сформулируйте правило умножения матриц. Выполните умножение матриц:

, ,

Ответы: , ,

3) Какими свойствами обладает операция умножения матриц: коммутативность, ассоциативность, дистрибутивнось ? Применяя нужные свойства, выполните умножение матриц:

Ответ:

4) Выполнить операцию возведения в степень Ответ:

Занятие 16. Обратная матрица. Системы линейных уравнений: метод обратной матрицы, метод Крамера

1) Дайте определение обратной матрицы и условия ее существования.Для указанных матриц проверьте выполнение условий существования обратной матрицы и, если обратная матрица существует, то найдите:

, ,

Ответы: ,

2. Системы линейных уравнений

Каждую систему линейных уравнений решите тремя способами:

• Методом обратной матрицы

• Методом Крамера

,

Занятие 17. Системы линейных уравнений: метод Гаусса ,ранг матрицы, теорема Кронекера-Капелли

1. Каждую систему линейных уравнений решите методом Гаусса:

2. Дайте определение понятия ранг матрицы. Найдите ранг матрицы методом элементарных преобразований:

а) , б) , в) , д)

3. Для каждой из указанных ниже систем

• методом элементарных преобразований определите ранг матрицы системы и ранг расширенной матрицы,

• на основании теоремы Кронекера-Капелли сделайте вывод о совместности системы (определите число решений системы),

• найдите решения системы, при этом, если решений множество, то укажите число базисных и свободных переменных

,

,

Ответы: не имеет решений, множество решений, .

Занятие 18. Векторы: линейные операции

1. По заданной паре векторо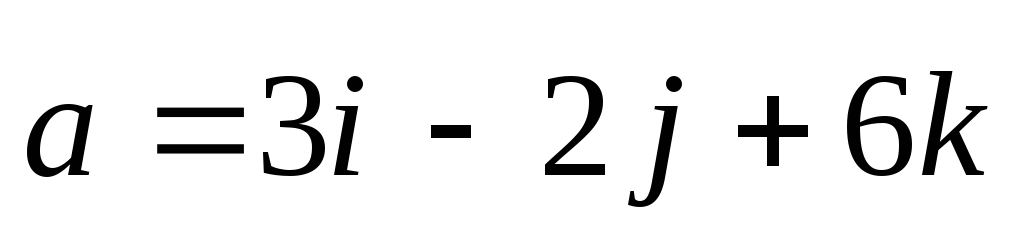в ,найти декартовы координаты векторов, их длину и соответствующие единичные векторы (орты), укажите направляющие косинусы.

2. При каких значениях параметров векторы,коллинеарны?

3. Даны смежные вершины параллелограмма и точка пересечения его диагоналей. Найдите координаты двух других вершин и длины сторон.Ответ:

4. По координатам середин сторон треугольника найдите координаты его вершин и длины сторон.

Ответ:

5. Координаты вершин треугольника ,,. Найти длину медианы, проведенной из вершины.

6. В трапеции 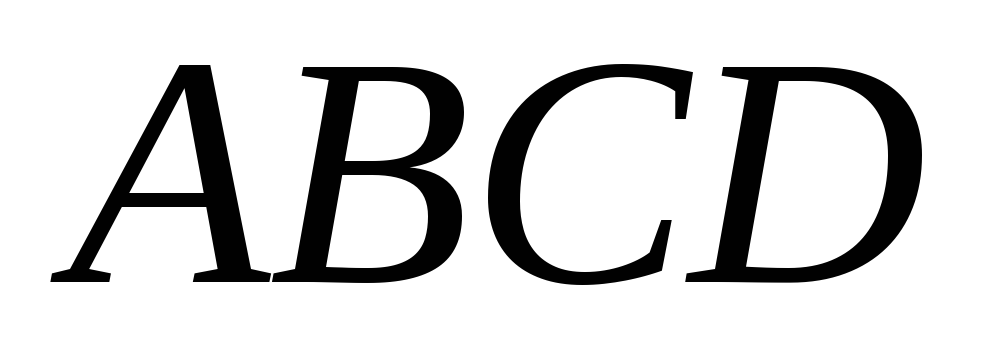отношение длин оснований, векторы диагоналей,. Выразить через векторывекторы сторон трапеции.Ответ: и т.д.

7. Найти координаты вектора относительно косоугольного базиса,,. Чему равны углы между векторами базиса?

8. Найти координаты вектора относительно косоугольного базиса,.Ответ:

Занятия 19. Векторы: скалярное произведение

9. При каких значениях векторыиортогональны?

10. Найти угол при вершине в треугольнике с вершинами,,.Ответ:

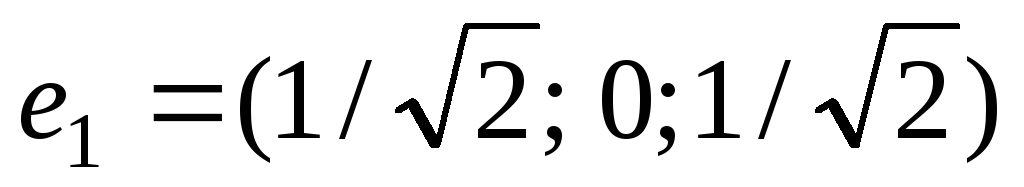11. Векторы образуют ортонормированный базис. Найти, если известныи.

12. Найдите длины диагоналей параллелограмма, построенного на векторах , если,.

Ответ:

13. Найдите проекцию , если.Ответ:

Занятия 20. Векторы: векторное и смешанное произведения

14. Найдите площадь параллелограмма, диагоналями которого служат векторы , где- единичные векторы под углом 45 градусов.Ответ:

15. Найт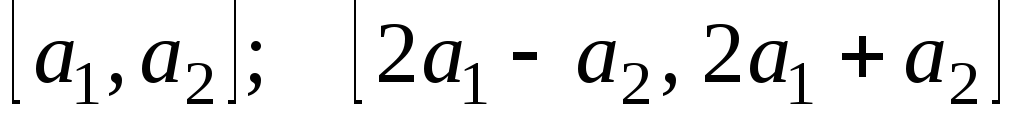и , если.Ответ:

16. Координаты вершин треугольника ,,. Найти площадь треугольника и длину его высоты, опущенной из вершины.

17. В точке приложена равнодействующая сил. Найдите вектор момента равнодействующей этих сил относительно точки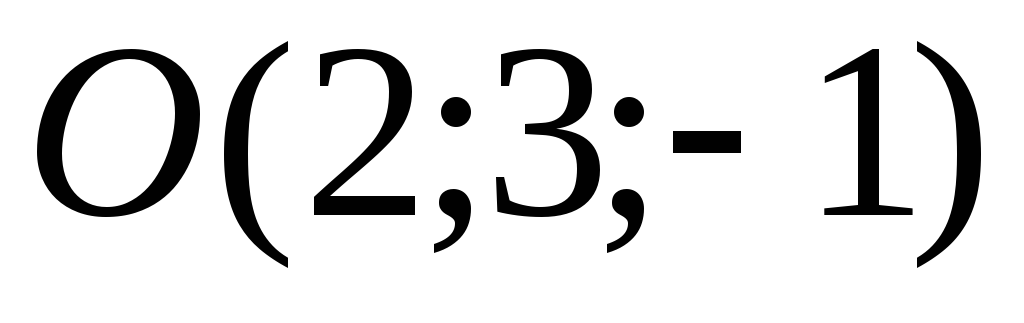.Ответ:

18. Определить, лежат ли точки в одной плоскости?

19. Найдите объем тетраэдра с вершинами .Ответ:

20. При каких значениях параметра векторыкомпланарны?

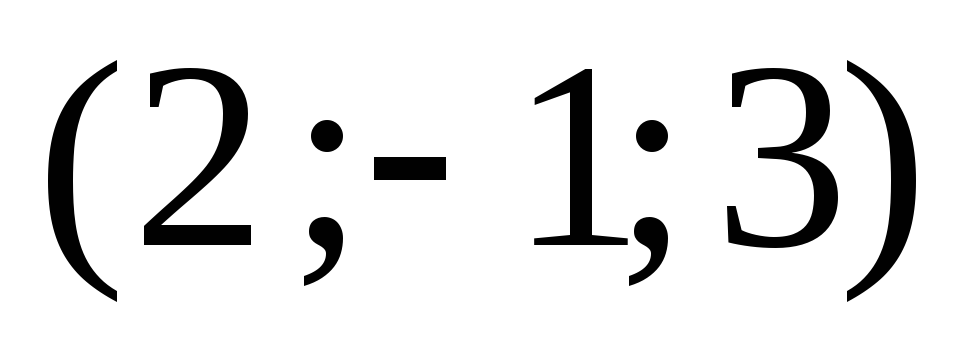
21. Координаты вершин тетраэдра ,,, а его объем равен 5. Найти значение неизвестной координаты.

Занятие 21. Прямая и плоскость в пространстве

1. Указать особенности в расположении плоскостей и схематично их построить:

а) 3Х–Z=0; б) 2Х=0; с) 2Х–6=0; ­д) Х–2У=0; е) Х–2У–2=0;

ж) 2Х+Z–2=0; з) 2Х+3У+2Z–6=0;

2. Составьте уравнение плоскости, проходящей через:

а) М(1; -1; 2) параллельно плоскости ОХУ;

б) М(4; -1; 2) и ось ОХ;

в) М₁(7; 2; -3); М₂(5; 6; -4) параллельно ОХ;

г) М₁(1; -1; 2); М₂(3; 0; -3) параллельно ;

д) М₁(1; -3; 2); М₂(5; 1; -4); С(2; 0; 3)

Найдите расстояние от М₀(1; 0; -2) до найденной плоскости

е) М₀(-2; 7; 3) параллельно плоскости Х–4У+5Z–1=0

ж) М₀(3; 4; 0) перпендикулярно плоскостям

Х+У+5Z–9=0; 2Х+У+2Z+1=0

3. Найти углы, образованные нормалью с координатными осями и найти расстояние плоскости от начала координат:

а) ; б);

4. Покажите, что плоскости параллельны и найдите расстояние между ними:

2Х–3У+6Z–14=0

4Х–6У+12Z+21=0;

5. Найдите угол между плоскостями:

Х–3У+6Z–14=0

2Х–У+Z=0.

6. Напишите уравнение прямой, проходящей:

а) М₁(2; 1; 3); М₂(3; 0; 1);

б) М₀(3; 1; 0)  ;

в) М₀(3; 1; 0)  плоскости 4Х+3У–Z=0;

7. Найдите точку М(Х; У; Z), симметричную М(1; 5; 2) относительно

плоскости 2Х–У–Z+11=0

8. Запишите канонические и параметрические уравнения прямой:

Ответы: Задача 2 б) 2У+Z=0; в) У+4Z+10=0; г) Х–2У–3=0; д) 11Х–5У+4Z–34 = 0; ;ж) 3Х–8У+Z+23=0;

4.; 7. M`(-3;7;4);

8. ;

Занятие 22. Прямая линия на плоскости

1. Написать уравнения прямой линии на плоскости: а) проходящей через произвольную точку под угломк оси ординат; б) проходящей через произвольную точкупараллельно прямой;

в) проходящей через произвольную точку перпендикулярно прямой;

г) пересекающей координатные оси в точках .

д) проходящей через начало координат и точку пересечения прямых .

2. В треугольнике с вершинами напишите уравнения сторон, высотыи медианы

3. По координатам смежных вершин и точки пересечения диагоналейнапишите уравнения сторон параллелограмма

4. Найдите точку, симметричную точке относительно прямой.Ответ:

5.Перепишите уравнение прямой линии в нормальном виде. Найдите направляющие косинусы нормали к прямой и расстояние от начала координат до прямой.

6.Покажите, что прямые линии параллельны и найдите расстояние между ними.Ответ: 3

Занятие 23. Кривые второго порядка

1. Уравнение описывает окружность радиуса 5 с центром в точке. Определить все коэффициенты этого уравнения.

2. Постройте кривые и укажите их основные характеристики

; ;

3. Установите, какие линии определяются уравнениями и схематично постройте эти линии:

• 

• 

• 

• 

• 

4. Составьте уравнение окружности , которая имеет центр на прямой и касается прямых.

Ответ:

Занятие 24. Контрольная работа «Векторная алгебра и аналитическая геометрия»

Занятие 25. Частные производные первого порядка. Градиент. Производная по направлению.

1. Найдите и схематично постройте область определения функции, дайте её характеристику (связность, замкнутость, ограниченность):

а) б) в)

г) д)

2. Найдите уравнение линии уровня (или поверхности уровня) для указанных функций, проходящих через заданные точки. Постройте линию уровня на чертеже вместе с областью определения:

а) б)

г) при условии

3. Для указанных функций найти частные производные первого порядка;

Записать полный дифференциал первого порядка.

а) б)

в) г)д)

е) ж)з)

и) к)

4. Найдите производную указанной функции по данному направлению в точке М₀:

а) если

б) по направлению

5. Найдите градиент функции в указанной точке:

а)

б)

в)

6. Найти нормаль к поверхности и написать уравнение касательной плоскости для указанной функции, в указанной точке:

а) в точках пересечения с прямой Х=У=2;

б)

Занятие 26. Локальные экстремумы функции двух переменных

1. Исследуйте функцию на локальный экстремум:

а) в)	б)

2. Исследуйте функцию на условный экстремум:

Z=6–5X–4У; (Х,У)=Х²-У²–9=0; L=6–5Х–4У+(Х²-У²–9)

3. Найдите наименьшее m и наибольшее М значения функции в замкнутой ограниченной области:

f=X2+У2–ХУ–Х–У, G: Х+У3, Х0, У0

Ответы: Задача 1: а) (-2;0) – минимум;

б) (4;4); (-4;-4) – минимумы; в) г)(1;-1;3) – минимум.

Задача 2.(5;-4); –max

(-5;4); –min

.

Задача 3. M=6; m=-1;