
- •Представление аналитических функций рядами. Понятие
- •Ряд Тейлора (разложение в ряд в окрестности точки аналитичности)
- •Изолированные особые точки аналитической
- •Вычет аналитической функции в изолированной
- •Вычет аналитической функции в изолированной особой точке
- •Вычисление контурных интегралов. Пример.
- •Вычисление несобственных интегралов. Примеры

Представление аналитических функций рядами. Понятие
вычета .
Лекция 9

Ряд Тейлора (разложение в ряд в окрестности точки аналитичности)
• |
|
( |
|
|
|
- точка аналитичности функции |
|
|
z |
ближайшая к особая точка ; |
|
|
Контур |
положительно ориентирован и охватывает точку |
|
|
|
||
|
|
и точку Функция аналитична на контуре внутри |
|
|
|
контура |
по интегральной формуле Коши: |
d = = =
Разложения в ряд для основных элементарных функций совпадают с их разложениями для функций действительного переменного.
Пример:

• |
Ряд Лорана (разложение в ряд в окрестности особой точки |
особая точка функции |
|
|
ближайшая к другая особая точка |
аналитичности – кольцо
Для применения интегральной формулы Коши область  аналитичности превращаем в односвязную, сделав разрез:
аналитичности превращаем в односвязную, сделав разрез:
=
;
=+
Главная часть Правильная часть |
|
||
Пример. Разложение |
|
|
= |
в в окрестности особой точки имеет вид |
|||
= . Область сходимости: |
|
||

Изолированные особые точки аналитической
функции
Точка• называется изолированной особой точкой функции, если однозначная функция аналитична в открытом круге за исключением самой точки В такой области функция однозначно представляется рядом Лорана, что и является основой классификации точек:
1.Устранимая особая точка - ряд Лорана содержит только правильную часть
Пример: для = точка устранимая
2. Существенно особая точка – ряд Лорана содержит бесконечное число членов
вглавной части ( отрицательных степеней):
+не существует
Пример: для существенно особая
3. Полюс порядка – главная часть ряда Лорана содержит членов:
+
Пример: для точка – полюс = 2, а – полюс = 1

Вычет аналитической функции в изолированной
особой точке
Рассматриваем• однозначную функцию , аналитичную в открытом круге за исключением самой точки
Находим интеграл по контуру , который охватывает точку и не проходит через другие особые точки:
Вычетом функции в точке называют коэффициент при разложения в ряд Лорана:
ВЫЧИСЛЕНИЕ ВЫЧЕТА. 1) В устранимой особой точке = 0 ; 2) В существенно особой точке вычет находят как коэффициент разложения в ряд:
=
3. В особой точке полюс порядка вычет можно найти как или по формулам: . или 

Вычет аналитической функции в изолированной особой точке
• |
Пусть функция аналитична в окрестности |
|
• |
бесконечно удаленной точки |
|
|
+ |
|
|
правильная часть |
главная часть |
Классификация точки по числу членов в главной части ряда Лорана: |
||
- устранимая особая точка |
|
|
2. + - полюс порядка |
|
|
3. +- существенно особая
ВЫЧЕТОМ функции азывают число при :
. Пример: =
= …

|
Основные теоремы о вычетах |
• |
Пусть функция аналитична на всей комплексной |
|
плоскости за исключением конечного числа особых |
|
точек Тогда справедливо: |
1.
или
2.  - – число особых точек, охваченных
- – число особых точек, охваченных
контуром .
Обе теоремы являются записью теоремы Коши для многосвязных областей через понятие вычета:



1) 2)

Вычисление контурных интегралов. Пример.
• |
по различным контурам |
Пример. Вычислим интеграл |
1)Ни одна из особых точек не попадает в область, охваченную контуром, и по теореме Коши ;
2). Все особые точки– простые полюсы попадают в область, охваченную контуром. Сумму вычетов во всех точках сразу в данном случае можно вычислить, используя вычет на бесконечности:
=;
3) Контур охватывает точки (простые полюсы).
Сумму вычетов в комплексно сопряженных точках удобно вычислить по формуле
= = =.
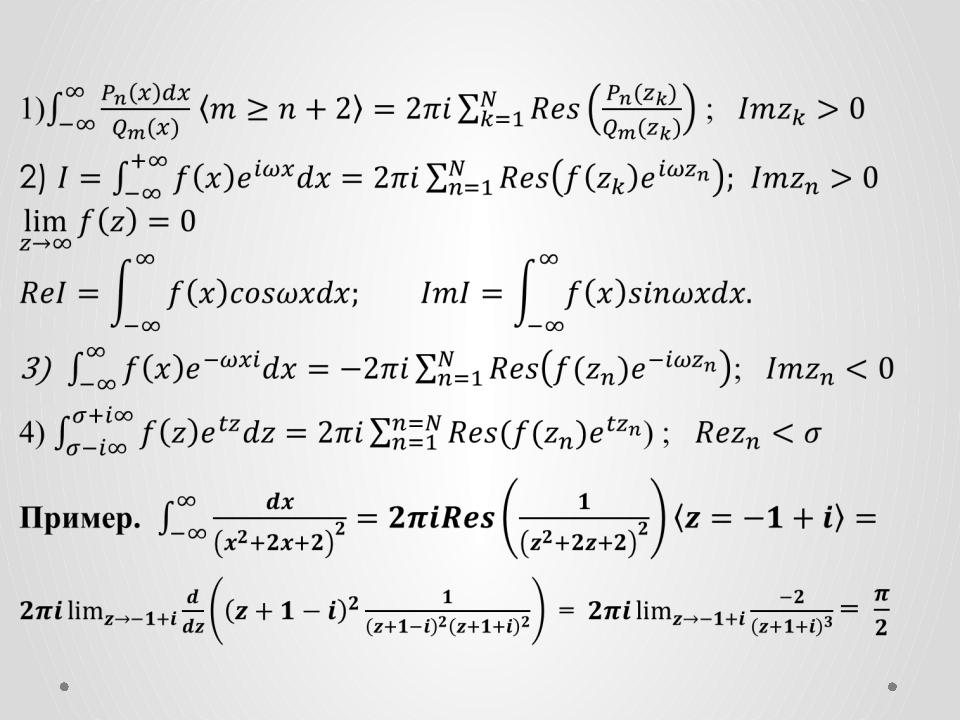
Вычисление несобственных интегралов. Примеры
1)• ;
2)
3);
4)) ;
Пример.
==
