Архив / Экстремумы

Применение производной

Задача 1

При каких значениях функция возрастает на всей числовой прямой?

Решение.

Находим производную: .

Функция будет возрастающей на множестве действительных чисел, если при любом . Поскольку является квадратным трехчленом с положительным коэффициентом при , то это условие будет выполнено, если дискриминант трехчлена не положителен при всех значениях переменной, т.е.

Задача 2.

Является ли прямая касательной к кривой ?

Решение.

Найдем общие точки прямой и кривой, решив уравнение

, . Получаем точки , .

Производная функции равна и её значения в точках пересечения равны , . Угловой коэффициент прямой равен 1. Следовательно данная прямая является касательной к кривой в точке .

Задача 3.

Правильная треугольная призма имеет объем 16 дм³. Найти длину стороны основания призмы с наименьшей полной поверхностью.

Решение.

Полная поверхность призмы вычисляется по формуле

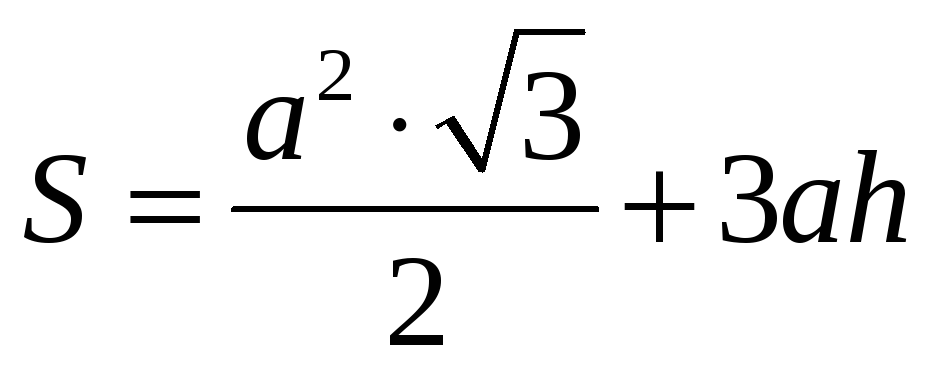, где - сторона основания, - высота призмы.

По условию задачи объем призмы равен 16 дм³, т.е. . Из последнего соотношения получаем высоту . А полную поверхность выражаем как функцию основания 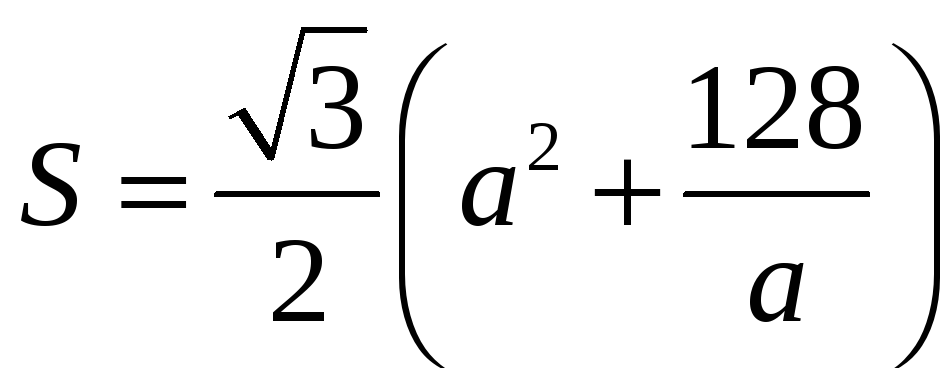, > 0, которую затем исследуем на экстремум. Находим производную , > 0 и ее критическую точку = 4 . На промежутке (0;4] производная , значит функция убывает. На промежутке

, и функция возрастает. Поэтому при = 4 функция принимает наименьшее значение.

Задача 4.

В правильной четырехугольной пирамиде сумма высоты и стороны основания равна 3. Найти наибольший возможный объем пирамиды.

Решение.

Пусть - сторона основания, - высота пирамиды, - объем пирамиды. Объем пирамиды можно вычислить по формуле .

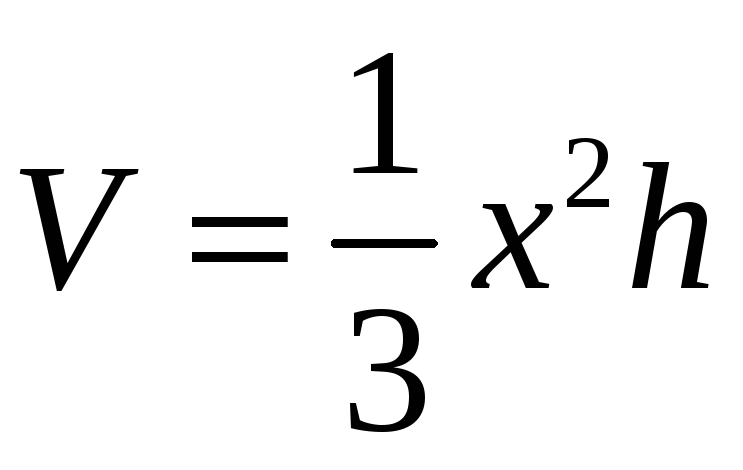По условию . Поэтому объем пирамиды выражаем как функцию стороны основания 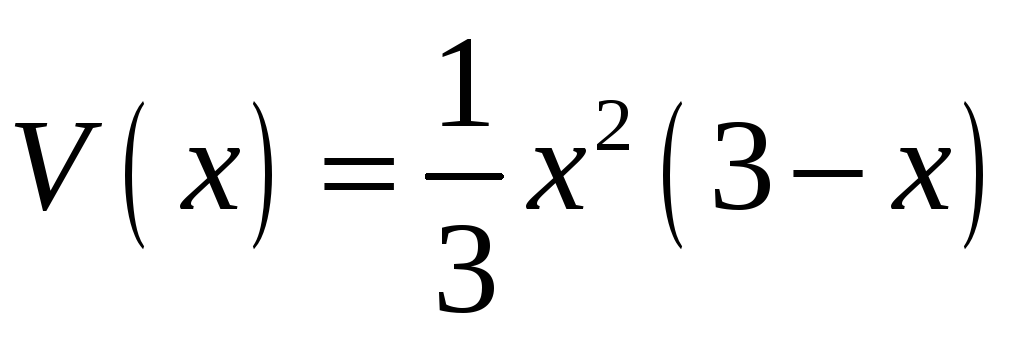, , и исследуем на экстремум: находим производную и критические точки , из которых условию задачи удовлетворяет только точка . Достаточные условия существования экстремума проверяем по знаку второй производной .

В точке = 2 вторая производная отрицательна .

Следовательно, при стороне основания равной 2 объем пирамиды наибольший.