
К.Р № 2 ПО МАТЕМАТИКЕ / 8196
.pdf
10
Продолжение таблицы 3
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
5 |
|
|
|
Гипербола |
|
|
|
|
|
|
|
|
|
|
|
|
x |
и y |
0 |
– координаты |
y |
b |
a |
|
с действительной |
|
x2 |
|
|
|
y2 |
|
x x |
2 |
|
y y |
2 |
0 |
|
центра, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
осью Ox |
|
|
|
|
|
|
1 |
0 |
|
0 |
1 |
a – действительная |
y0 |
|
|
|
||||
|
a2 |
|
|
b2 |
a2 |
b2 |
|
|
|
|||||||||||
или ей |
|
|
|
|
|
|
|
|
|
|
полуось, |
|
|
|
|
|||||
параллельной |
|
|
|
|
|
|
|
|
|
|
|
|
b – мнимая полуось |
|
x0 |
x |
|
|||
Гипербола |
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
и y0 – координаты |
y |
b |
a |
|
||
с действительной |
|
y2 |
|
|
|
x2 |
|
y y0 2 |
|
x x0 |
2 |
|
|
|
центра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
осью Oy |
|
|
|
|
|
|
b – действительная |
y0 |
|
|
|
|||||||||
|
b2 a2 |
1 |
|
1 |
|
|
|
|||||||||||||
или ей |
|
b2 |
|
a2 |
|
|
полуось, |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a – мнимая полуось |
|
|
|
|
||||
параллельной |
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Парабола |
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
и y0 – координаты |
y |
p<0 |
p>0 |
|
||
с осью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y2 2 px |
y y0 2 |
2 p x x0 |
|
|
|
|
|||||||||||||
симметрии Ox |
|
|
вершины, |
y0 |
|
|
|
|||||||||||||
или ей |
|
|
|
|
|
|
|
|
|
|
|
|
p – параметр параболы |
|
|
|
|
|||
параллельной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
x |
|
Парабола |
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
и y0 – координаты |
y |
p>0 |
x0 x |
|
||
с осью |
|
x2 2 py |
x x0 2 |
2 p y y0 |
|
|
|
|||||||||||||
симметрии Oy |
|
|
|
вершины |
y0 |
|
|
|
||||||||||||
или ей |
|
|
|
|
|
|
|
|
|
|
|
|
p – параметр параболы |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p<0 |
|
|
|||||
параллельной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

11
ЗАДАЧА 5. Найти неопределенные интегралы. Следует запомнить основные интегралы и их свойства:
1. dx x C. |
|
6. еxdx ex C |
|
||||||||||||||||||||
|
xndx |
x |
n 1 |
C,( n 1) |
7. |
|
|
dx |
|
|
tgx C. |
|
|||||||||||
2. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||
n 1 |
cos |
x |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3. |
|
dx |
ln |
|
x |
|
C |
8. |
|
|
dx |
|
|
ctgx C. |
|
||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
sin2 x |
|
|||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4. |
sin xdx cos ax C. |
9. |
|
|
dx |
|
|
arctgx C. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5. |
cos xdx sin ax C. |
10. |
|
|
|
dx |
|
|
arcsin x |
C. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|||||||
Постоянный множитель можно выносить за знак интеграла:
kf ( x )dx k f ( x )dx.
Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций:
( f1 f2 )dx f1dx f2dx.
Рассмотрим применение формулы №2 таблицы интегралов.
Пример 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x2dx |
x2 1 |
|
C |
x3 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
dx x 2dx |
x 2 1 |
C |
x 1 |
|
C |
1 |
C |
|
||||||||||||||||||||
x2 |
2 1 |
1 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||||||||||||
Пример 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
x1 3 1 |
|
C |
x4 3 |
C |
3x4 3 |
C |
|
|||||||||||||||||||
|
xdx x1 3dx |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 3 1 |
|
|
4 3 |
|
|
4 |
|
|
|
||||||||||
Пример 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
dx x |
2 5dx |
x 2 5 1 |
|
C |
x3 5 |
C |
5x3 5 |
C |
|||||||||||||||||
5 |
|
|
|
|
2 5 1 |
|
|
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 5 |
|
|
|
|
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим применение основных свойств интегралов.
Пример 5.

|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
2xdx 2 x1dx 2 |
x1 1 |
|
C 2 |
x2 |
C x2 C |
|
|
||||||||||||
1 1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
Пример 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
cos x tgx dx cos xdx |
1 |
dx C sin x ln x C |
|
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
Пример 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
5x 4 |
3x2 1 dx 5 |
|
x 4 dx 3 x2 dx |
|
dx x5 |
x3 |
x C |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
3 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||
6x3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 x3dx 3 x 1 2dx 2 dx 6 x4 3 2x1
2dx 2 dx 6 x4 3 2x1 2 2x C
2 2x C
4
Рассмотрим применение формулы f kx b 1kF kx b C .
Другими словами, если в подынтегральной функции x умно-
жен на число k, то перед интегралом следует писать множитель 1k .
Пример 9.
sin 5x dx 15 cos 5x C
Пример 10. |
|
|
|
|
|
|
|
|
|
|
|||
1 |
dx |
1 |
|
|
|
2x 1 |
|
C |
|
||||
|
|
|
|
|
|||||||||
|
|
|
ln |
|
|
||||||||
2x 1 |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Пример 11. |
|
|
|
|
|
|
|
|
|
|
|||
3x 2 4 dx |
1 |
|
|
3x 2 5 |
C |
||||||||
|
|
|
|
|
|
||||||||
|
3 |
5 |
|||||||||||
|
|
|
|
|
|
|
|||||||
Важным способом интегрирования является подведение под знак дифференциала.
Дифференциал функции одной переменной u равен произведению ее производной на dx, то есть: du u dx .
Например, u x2 , du 2x dx .
Вид интеграла не изменится, если вместо x и dx в нем будут присутствовать функция u f x и du , то есть: f u du F u C .
Пример 12.

|
|
|
|
|
|
13 |
|
|
|
|
|||
sin5 x cos x dx |
u sin x |
|
|
|
|
||||||||
du cos x |
dx |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
u5du |
u6 |
C |
sin6 x |
C |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
6 |
|
|
6 |
|
|
|
|
|
|
||||
Пример 13. |
|
|
|
|
|
|
|
||||||
x sin x2 1 dx |
u x2 1 |
|
1 |
sin u du |
1 |
cos u |
|||||||
du 2xdx |
2 |
2 |
|||||||||||
|
|
cos x2 1 C . |
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
||
ЗАДАЧА 6. Найти площадь фигуры, ограниченной линиями. Для решения этой задачи следует использовать определенный
интеграл, вычисление которого производится по формуле:
|
|
|
|
|
|
|
b |
f x dx F( x ) |
|
b |
F b F a . |
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим применение этой формулы. |
|||||||||||||||||
Пример 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
3 |
|
2 |
|
|
3 |
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
x2dx |
x |
|
|
|
|
|
2 |
|
|
|
1 |
|
7 |
2,3. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
3 |
|
|
1 |
|
3 |
3 |
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь вместо x подставляем сначала верхнюю границу x 2 , затем нижнюю границу x 1, между выражениями ставим знак «минус».
Пример 2.
3 |
|
|
|
|
3 |
3 |
3 |
3 |
|||
4x 3 dx 4xdx |
3dx 4 xdx 3 dx |
||||||||||
1 |
1 |
1 |
1 |
1 |
|||||||
4 |
x2 |
|
|
3 |
3x |
|
31 2 32 2 1 2 3 3 3 1 16 12 4 . |
||||
|
|||||||||||
|
|
|
|
||||||||
2 |
1 |
||||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
Пример 3. Найти площадь фигуры, ограниченной линиями: y 2x , y 3 x2 .
Площадь фигуры, расположенной между двумя линиями находится по формуле:
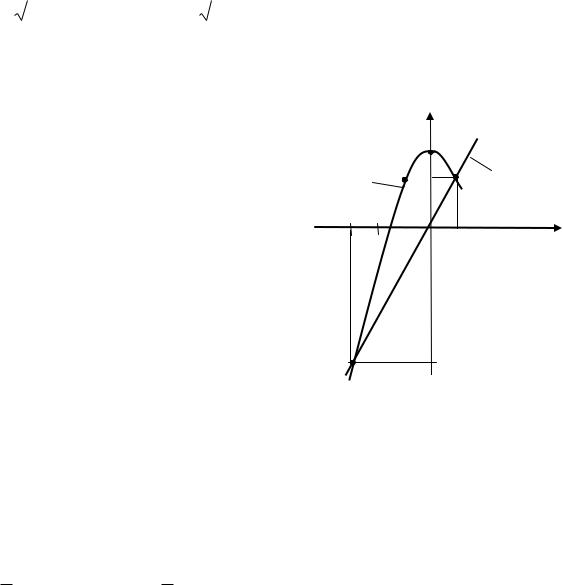
14
b
S yв yн dx , a
где yв и yн – уравнения соответственно верхней и нижней линий,
ограничивающих фигуру; а и b – точки пересечения линий.
Найдем точки пересечения этих линий, для чего приравняем правые части уравнений:
2x 3 x2 x2 2x 3 0 .
|
|
|
Найдем |
|
|
дискриминант и |
корни: |
|
|
D 22 4 3 16 , |
|||||||||||||||||||||||||
x 2 |
16 |
3, x |
2 |
2 |
16 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Построим линии между точками пересечения, для чего зада- |
||||||||||||||||||||||||||||||||
дим несколько значений x |
и найдем соответствующие y. |
|
|||||||||||||||||||||||||||||||||
|
|
|
1) |
y 2x , это прямая, постро- |
|
|
|
|
|
|
|
|
|
|
|
y |
|
||||||||||||||||||
им ее по двум точкам. |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x |
|
-3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
yн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y |
|
-6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y 3 x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2) |
|
это парабола, |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
возьмем несколько точек. |
|
|
|
–3 |
|
|
|
|
|
|
|
|
|
1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x |
|
-3 |
|
-1 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y |
|
-6 |
|
2 |
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Из рисунка видим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
yв 3 x2 , yн 2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–6 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Найдем площадь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
S y |
|
|
y |
|
dx |
3 x2 2x dx 3x |
|
|
x2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
в |
н |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
3 1 |
1 |
12 |
|
|
3 |
3 3 |
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 23 9 9 9 1 23 9 10,7 ед.кв.

15
ЗАДАЧА 7. Решить дифференциальные уравнения. Дифференциальным уравнением (ДУ) 1-го порядка называется
уравнение, содержащее первую производную y неизвестной функции y f x , которую надо найти. Основным видом ДУ 1 порядка являются уравнения с разделяющимися переменными, которые имеют вид: y x y . Алгоритм решения этих уравнений выглядит следующим образом:
1)записывается, что y dydx ;
2)выражения с x переносятся в одну сторону, с y – в другую, то есть разделяются;
3)интегрируются обе части равенства.
Пример 1.
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
dy |
|
|
|
y |
|
|
dy |
|
y |
|
dx |
|
dy |
|
|
1 |
dx . |
|||||
dx |
|
x |
|
x |
|
|
|
|
x |
|||||||||||||
|
|
|
|
y |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Переменные разделены, интегрируем обе части:
|
dy |
|
|
|
1 |
dx , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
|
|
|
|
|
||||
|
y |
|
|
|
|
|
||||||
|
dy |
|
|
|
1 2 dy |
y 1 2 1 |
2 y1 2 |
|
||||
|
|
|
y |
2 |
y |
, |
||||||
|
|
|
|
1 2 1 |
||||||||
|
y |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
1x dx ln x C ,
приравниваем полученные выражения и получаем ответ: 2
 y ln x C
y ln x C
Пример 2. |
|
|
|
|
|
|
|||||
|
y |
|
|
ln x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
2 y 1 5 x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
|
dy |
|
ln x |
dy |
ln x |
dx |
2 y 1 5 dy |
ln x |
dx |
||
|
|
|
|
|
|||||||
|
dx |
x 2 y 1 5 |
x 2 y 1 5 |
x |
|||||||
Переменные разделены, интегрируем:
2 y 1 5dy lnxx d x .

|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
2 y 1 5dy |
1 |
2 y 1 6 , |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
||
|
ln x |
d x |
|
u ln x |
dx |
u du |
u2 |
C |
ln2 x |
C . |
|||||||
|
|
du |
|
1 |
|
|
|
|
|||||||||
x |
2 |
|
2 |
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: |
1 |
2 y 1 6 |
|
ln2 x |
C . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
6 |
|
|
|
2 |
|
|
|
|
|
|
||
Дифференциальным уравнением (ДУ) 2-го порядка называется |
|||||||||||||||||
уравнение, |
содержащее вторую производную |
y неизвестной |
|||||||||||||||
функции y f x , которую надо найти.
Рассмотрим решение уравнений y f x , допускающих понижение порядка. Путем интегрирования, последовательно находятся первая производная y , а затем функция y .
Пример 3. y sin5x ,
y sin 5x dx |
1 |
cos5x C1, |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
||||
y |
|
|
|
|
|
|
cos 5x C |
dx |
|
|
|
cos 5x dx C |
|
dx |
|
|
|
|
|
sin x C x C |
|
|||
|
|
|
|
|
5 |
|
|
|
|
|
|
|||||||||||||
|
|
|
5 |
|
1 |
|
|
|
1 |
|
5 5 |
1 |
2 |
|||||||||||

17
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ №2
ЗАДАЧА 1. Решить систему линейных алгебраических урав- |
|||||||
нений методом Гаусса. |
|
|
|
|
|||
|
1.1. |
х у 2z 1 |
1.6. |
|
х у 3 |
|
|
|
|
|
|
|
|
3x 2 y z 1 |
|
|
|
3x y 4z 1 |
|
|
|
||
|
|
|
4x z 1 |
|
4x 3y z 2 |
|
|
|
|
|
|
|
|
|
|
|
1.2. |
х у 2z 1 |
1.7. |
х 2 у z 0 |
|
||
|
|
|
|
|
|
3x y 4 |
|
|
|
3x y 4z 5 |
|
|
|
||
|
|
|
4x y 3 |
|
4x 3y z 4 |
|
|
|
|
|
|
|
|
|
|
|
1.3. |
|
х у z 0 |
1.8. |
|
4х у 4 |
|
|
|
|
3x y 3 |
|
|
|
|
|
|
|
|
2x 2 y z 1 |
|
||
|
|
4x 3y 3z 3 |
|
|
3y z 3 |
|
|
|
|
|
|
|
|
|
|
|
1.4. |
х у 2z 3 |
1.9. |
х у 2z 3 |
|
||
|
|
|
3x y z 1 |
|
|
|
|
|
|
|
|
3x y 6z 1 |
|
||
|
|
2x 2 y z 6 |
|
|
4x z 1 |
|
|
|
|
|
|
|
|
|
|
|
1.5. |
х 2 у z 2 |
1.10. |
|
х у 2z 1 |
|
|
|
|
|
|
|
|
|
|
|
|
3x 3y z 0 |
|
3x 2 y 4z 1 |
|
||
|
|
|
2x y 2 |
|
|
4x 3y z 1 |
|
|
|
|
|
|
|
||
|
ЗАДАЧА 2. Выполнить операции с матрицами. |
||||||||||
2.1. |
|
1 |
4 |
1 |
4 |
3 |
3 |
5 |
|||
|
|
A |
|
|
, B |
|
|
|
, С |
|
. |
|
|
|
5 |
2 |
|
7 |
2 |
6 |
|
1 |
2 |
|
|
Найти: 3В, 2А–3С, |
А В |
|
|
|
|
||||
2.2. |
|
1 |
2 |
2 |
3 |
4 |
5 |
4 |
|||
|
|
A |
|
|
, B |
|
|
, С |
|
. |
|
|
|
|
3 |
4 |
|
0 |
1 6 |
|
3 |
7 |
|
|
|
Найти: –3В, 2А+4С, |
С В |
|
|
|
|
||||
2.3. |
|
0 |
2 |
1 |
3 |
2 |
6 |
3 |
|||
|
|
A |
|
|
, В |
|
|
, С |
|
|
. |
|
|
|
3 |
2 |
|
4 |
2 |
|
4 |
1 5 |
|
|
|
Найти: 5С, 2А–4В, |
А В |
|
|
|
|
||||

|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2.4. |
1 |
3 |
4 |
2 |
|
3 |
5 |
|
0 |
|
|||
|
A |
|
|
, В |
|
, С |
|
|
|
. |
|
||
|
|
0 |
2 |
|
6 |
3 |
|
1 |
2 |
|
6 |
|
|
|
Найти: –3С, 2В–3А, |
В С |
|
|
|
|
|
|
|
||||
2.5. |
2 |
0 |
4 |
|
2 |
3 |
|
7 |
4 |
|
|||
|
А |
|
|
, |
В |
|
, С |
|
|
. |
|
||
|
|
6 |
1 5 |
|
4 |
6 |
|
0 |
|
1 |
|
||
|
Найти: |
–4А, 2В+3С, |
В А |
|
|
|
|
|
|
|
|||
2.6. |
3 |
10 |
1 |
|
1 |
6 |
|
4 |
|
3 |
|
||
|
А |
|
|
, |
В |
|
, С |
|
|
. |
|
||
|
|
4 |
1 5 |
|
4 |
2 |
|
2 |
|
5 |
|
|
|
|
Найти: –5А, 2С–3В, В С |
|
|
|
|
|
|
|
|||||
2.7. |
2 |
5 |
1 |
|
1 |
9 |
1 |
|
|
4 |
3 |
||
|
А |
|
|
, |
В |
|
, С |
|
|
|
. |
||
|
|
4 |
1 3 |
|
5 |
2 |
4 |
|
|
2 |
6 |
|
|
|
Найти: |
–4С, 2А–3В, |
С А |
|
|
|
|
|
|
|
|||
2.8. |
2 |
5 |
1 |
|
1 |
9 |
1 |
|
|
4 |
3 |
||
|
А |
|
|
, |
В |
|
, С |
|
|
|
. |
||
|
|
4 |
1 3 |
|
5 |
2 |
4 |
|
|
2 |
6 |
|
|
|
Найти: |
–4С, 3В–2А, |
С В |
|
|
|
|
|
|
|
|||
2.9. |
3 |
2 |
1 |
2 |
|
4 |
1 |
|
|
|
|
||
|
A |
|
|
, В |
|
, С |
|
|
. |
|
|
||
|
|
1 |
4 |
|
5 |
3 |
|
7 |
3 |
|
|
|
|
|
Найти: 3А, 2В–4С, А С |
|
|
|
|
|
|
|
|||||
2.10. |
0 |
2 |
1 |
2 |
|
4 |
1 |
|
|
|
|
||
|
A |
|
|
, В |
|
, С |
|
. |
|
|
|
||
|
|
1 |
5 |
|
5 |
4 |
|
6 |
3 |
|
|
|
|
|
Найти: 4В, |
3А+2С, В С |
|
|
|
|
|
|
|
||||
ЗАДАЧА 3. Найти минимальное и максимальное значение це-
левой функции при заданных ограничениях. |
|
|
|
|
||||||
|
|
|
|
|
||||||
3.1. |
F( x ) 4x1 3x2 |
3.6. |
|
F( x ) 7x1 x2 |
||||||
|
|
2x1 x2 4 |
|
|
x1 4x2 58 |
|||||
|
|
x1 3x2 37 |
|
|
|
|
|
|
||
|
|
|
|
2x1 x2 28 |
||||||
|
|
|
|
|
|
|
|
4x2 20 |
||
|
4x1 9x2 20 |
|
|
5x1 |
||||||
|
|
x 0, x |
2 |
0 |
|
|
x |
0, x |
2 |
0 |
|
|
1 |
|
|
|
1 |
|
|
||

|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3.2. |
F( x ) 3x1 2x2 |
|
3.7. |
F( x ) x1 4x2 |
||||||||||||||
|
4x1 5x2 29 |
|
|
3x1 2x2 12 |
||||||||||||||
|
|
3x1 x2 14 |
|
|
|
2x1 x2 18 |
||||||||||||
|
|
|
|
|
||||||||||||||
|
|
5x 2x |
2 |
38 |
|
|
x 4x |
2 |
16 |
|||||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
||||
|
|
x 0, x |
2 |
0 |
|
|
|
x |
0, x |
2 |
0 |
|||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
3.3. |
F( x ) 2x1 3x2 |
|
3.8. |
F( x ) 5x1 4x2 |
||||||||||||||
|
x1 x2 8 |
|
|
|
x1 2x2 4 |
|||||||||||||
|
|
|
x1 5 |
|
|
|
|
|
|
|
7x2 28 |
|||||||
|
|
|
|
|
|
|
|
2x1 |
||||||||||
|
|
|
x 2 |
|
|
|
|
|
x 4x |
2 |
12 |
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
x 0,x |
2 |
0 |
|
|
|
x |
0, x |
2 |
0 |
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
3.4. |
F( x ) 5x1 7x2 |
|
3.9. |
F( x ) 5x1 x2 |
||||||||||||||
|
3x1 14x2 78 |
|
|
6x1 3x2 34 |
||||||||||||||
|
|
5x1 6x2 26 |
|
|
|
|
3x2 38 |
|||||||||||
|
|
|
|
2x1 |
||||||||||||||
|
|
|
x 4x |
2 |
26 |
|
|
3x 4x |
2 |
12 |
||||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
x 0, x |
2 |
0 |
|
|
x |
0, x |
2 |
0 |
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
3.5. |
F( x ) 5x1 3x2 |
|
3.10. |
F( x ) x1 x2 |
||||||||||||||
|
6x1 5x2 17 |
|
|
5x1 2x2 4 |
||||||||||||||
|
|
x1 2x2 34 |
|
|
|
2x1 |
5x2 60 |
|||||||||||
|
|
|
|
|
||||||||||||||
|
4x 9x |
2 |
17 |
|
|
x 4x |
2 |
12 |
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
x 0, x |
2 |
0 |
|
|
|
x |
0, x |
2 |
0 |
|||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
ЗАДАЧА 4. Привести уравнение кривой к каноническому виду
ипостроить линию.
4.1.а) x2 y 2x 5 0 , б) x2 y 2 2 y 5 0 , в) x2 y 2 2 y 3 0
4.2.а) x2 y 2 4x 0 ,
б) x2 y 2x 5 0 , в) x2 y 2 2x 8 0
