
К.Р № 2 ПО МАТЕМАТИКЕ / 8196
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Кузбасский государственный технический университет имени Т. Ф. Горбачева
Кафедра математики
И. А. Ермакова, В. А. Гоголин
МАТЕМАТИКА
Методические указания к контрольной работе №2 для студентов заочной формы обучения
Рекомендованы учебно-методической комиссией направления 080200.62 «Менеджмент»
вкачестве электронного издания для самостоятельной работы
Кемерово 2014
1
Рецензент
Волков В. М. – доцент кафедры математики
Ермакова Инна Алексеевна, Гоголин Вячеслав Анатольевич. Ма-
тематика: методические указания к контрольной работе №2 для студентов направления подготовки бакалавров 080200.62 «Менеджмент» профиль 080206.62 "Производственный менеджмент" заочной формы обучения [Электронный ресурс] / И. А. Ермакова, В. А. Гоголин. – Электрон. дан. – Кемерово: КузГТУ, 2014. – Систем. требования: любой компьютер, поддерживающий Microsoft Windows-97 и выше, мышь. – Загл. с экрана.
Приводятся задания и методические указания по их решению по темам, изучаемым во 2 семестре. Выполнение заданий, изложенных в методических указаниях, позволяет студенту качественно подготовиться к зачету, вопросы к которому прилагаются.
© КузГТУ, 2014 © Ермакова И. А., Гоголин В. А., 2014
2
Дисциплина «Математика» изучается в течение трех семестров. Во втором семестре студенты заочной формы обучения выполняют контрольную работу №2.
Студент выполняет контрольную работу, выбирая вариант задания по последней цифре зачетной книжки. Если последняя цифра равна 0, то студент решает вариант №10. Работа, выполненная не по своему варианту, не проверяется.
Работу следует выполнять в рукописном виде.
Решения задач должны иметь объяснения в соответствии с методическими указаниями. При отсутствии письменных объяснений, студент должен быть готов дать устные пояснения к решению задач.
ПРОГРАММА 2 СЕМЕСТРА
Раздел 3. Элементы линейной алгебры
3.1.Матрицы и действия над матрицами. Использование матриц в экономике.
3.2.Определители и их свойства. Вычисление определителей.
3.3.Решение систем линейных уравнений. Метод Крамера. Обратная матрица. Матричный способ решения систем линейных уравнений.
3.4.Ранг матрицы. Исследование систем линейных уравнений. Метод Гаусса. Однородные системы.
3.5.Использование алгебры матриц в экономике. Модель Леонтьева. Составление межотраслевого баланса.
Раздел 4. Векторная алгебра
4.1.Понятие n-мерного линейного пространства. N-мерные векторы, действия над ними. Линейные операторы. Собственные значения матриц и собственные векторы. Линейная модель торговли.
4.2.Координаты вектора в пространстве. Линейная независимость векторов. Базис. Разложение по базису.
4.3.Скалярное и векторное произведения векторов. Использование в экономике.
Раздел 5. Элементы аналитической геометрии
5.1.Прямая линия на плоскости. Линейные функции спроса и предложения. Точка рыночного равновесия..
5.2.Плоскость и прямая в пространстве.
5.3.Кривые второго порядка.
3
5.4. Задачи линейного программирования. Построение математических моделей. Графический метод решения задач линейного программирования. Роль математического программирования при решении управленческих задач.
Раздел 6. Интегральное исчисление
6.1. Неопределенный интеграл, свойства. Методы интегрирования: по частям и заменой переменных. Таблица основных интегралов. 6.2. Определенный интеграл, основные свойства. Формула Ньюто- на-Лейбница. Методы интегрирования. Геометрические приложения определенного интеграла. Приложение интегралов в экономике.
Раздел 7. Дифференциальные уравнения
7.1.Дифференциальные уравнения первого и второго порядка. Линейные дифференциальные уравнения с постоянными коэффициентами.
7.2.Использование дифференциальных уравнений в экономике.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
ЗАДАЧА 1. Решить систему линейных алгебраических уравнений методом Гаусса.
х у 2z 43x y 4z 2
4x y z 1
Выразим из любого уравнения любую неизвестную (ту, которую легче выразить) и подставим ее в два других уравнения.
Из первого уравнения: x 4 y 2z , подставим его в 1-е и 2-е
уравнения. Получим:
3 4 y 2z y 4z 24 4 y 2z y z 1 .
Раскроем скобки:
12 3y 6z y 4z 216 4 y 8z y z 1 .
Приведем подобные:
2 y 10z 10
3y 9z 15 .
4
Выразим из одного уравнения любую переменную (ту, которую легче выразить) и подставим ее в другое уравнение.
Из 1-го уравнения: 2 y 10 10z , откуда y 5 5z . Подста-
вим во 2-е уравнение и получим:
3 5 5z 9z 15 15 15z 9z 15 6z 0 z 0 .
Далее найдем y 5 5z 5 5 0 5.
Теперь найдем x 4 y 2z 4 5 2 0 1. Получили: x 1, y 5, z 0 .
Сделаем проверку, подставим найденные значения в исходную систему уравнений:
1 5 2 0 43 1 5 4 0 2
4 1 5 0 1
Так как все равенства верные, то система решена верно.
ЗАДАЧА 2. Выполнить операции с матрицами. |
|
|
|
|
||||
3 |
2 |
4 |
6 5 |
2 |
4 |
|||
Заданы матрицы A |
|
, B |
|
, |
С |
|
|
. |
1 |
0 |
8 |
4 |
7 |
|
5 |
1 |
|
Найти: 2А, 3С–2А, А В.
Произведением матрицы A порядка m n на число называется матрица A A того же порядка, элементами которой являются произведения соответствующих элементов матрицы A на число .
3 2 |
2 2 |
6 |
4 |
|||||
2A |
1 |
2 |
0 2 |
|
|
2 |
0 |
. |
|
|
|
|
|||||
Суммой (разностью) двух матриц A и B одинакового порядка называется матрица того же порядка, элементы которой являются
суммой (разностью) соответствующих элементов матриц |
A и B . |
||||||||
Тогда: |
|
|
|
|
|
|
|
|
|
2 3 |
4 3 |
3 4 |
2 4 |
6 12 |
|
12 |
8 |
|
18 |
3С 4А |
|
|
|
|
|
|
|
|
|
5 3 |
1 3 |
1 4 |
0 4 |
15 3 |
|
4 |
0 |
|
19 |
4
3
Произведением матрицы A порядка m n на матрицу B порядка n p называется матрица порядка m p , элементы которой
5
представляют собой сумму попарных произведений элементов строки матрицы A на элементы j-го столбца матрицы B .
Пусть А В D . |
|
|
|
|
|
|
|
||
Определим размеры матриц и найдем произведение: |
|
||||||||
|
3 2 |
|
B2x3 |
4 |
6 |
5 |
|
D A2x2 B2x3 |
D2x3 |
A2x2 |
1 0 |
, |
|
4 |
|
, |
|||
|
|
|
8 |
7 |
|
|
|
||
3 4 2 8 |
3 6 2 ( 4 ) |
3 5 2 7 |
28 10 |
29 |
||||||
|
|
|
|
|
|
|
|
|
. |
|
|
1 4 |
0 8 |
1 6 0 ( 4 ) |
1 4 0 7 |
|
|
4 |
6 |
5 |
|
|
|
|
|
|||||||
i-й
ЗАДАЧА 3. Решить задачу линейного программирования графическим методом. Найти минимальное и максимальное значение целевой функции F x при заданных ограничениях.
F x x1 2x2 ,
x1 x2 10,x2 8,
x2 2,
x1 0, x2 0.
Построим область решений в системе координат x1Ox2 . Выпишем каждое неравенство и найдем область, которую оно задает.
1) x1 x2 |
10 . |
|
Запишем |
в виде равенства: |
x1 x2 10 , откуда выразим |
x2 10 x1 . Это уравнение прямой, |
построим ее по двум точкам. |
|
Зададим два значения x1 и найдем соответствующие значения x2 :
|
x1 |
0 |
5 |
|
|
|
x2 10 x1 |
10 |
5 |
|
и 5; 5 , которые |
Получили две точки с координатами 0;10 |
|||||
отложим на чертеже и соединим прямой линией (рис.1). Эта прямая разбила всю плоскость на две области: одна область выше, а другая
– ниже прямой. Чтобы найти искомую область, где x1 x2 10 , возьмем любую точку, не лежащую на прямой линии, и подставим ее координаты в неравенство. Если неравенство выполняется, то взятая точка лежит в искомой области. Если неравенство не выполняется, то следует выбрать область с другой стороны линии.
В данном случае удобно взять точку О 0; 0 – начало координат. Для нее: x1 0 и x2 0. Подставим эти значения в неравен-

|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
||
ство: x1 x2 10 |
|
|
|
0 0 10 – верно. Точка О 0; 0 лежит в ис- |
|||||||||||||||||||||
комой области, наносим штриховку в ее сторону. |
|
||||||||||||||||||||||||
x2 |
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
B C |
|
|
|
|
x1 x2 10 |
|
||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
A |
|
D |
|
|
|
|
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
8 |
10 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
grad F 1; |
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2) x2 8 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Запишем равенство: |
x2 8 . |
|
Это |
уравнение горизонтальной |
|||||||||||||||||||||
прямой, отсекающей на оси OX 2 отрезок, равный 8. Построим ее на том же чертеже (см. рис.1).
В искомой области x2 8 , поэтому заштрихуем область, лежащую ниже этой прямой.
3) x2 2 .
Запишем равенство: x2 2 . Это уравнение горизонтальной прямой, отсекающей на оси OX 2 отрезок, равный 2. Построим прямую (см. рис.1).
В искомой области x2 2 , поэтому заштрихуем область, лежащую выше этой прямой.
4) x1 0 и x2 0 .
Здесь x1 0 и x2 0 – это уравнения координатных осей
(см. рис.1).
Так как x1 0 , нанесем штриховку вправо от прямой x1 0. Так как x2 0 , нанесем штриховку вверх от прямой x2 0.
7
Область АВСD, в которой пересекаются все штриховые линии, является искомой. Так как все неравенства нестрогие, то все прямые линии входят в искомую область.
Далее найдем градиент целевой функции F x x1 2x2 . Его координаты равны коэффициентам перед переменными x1 и x2 в выражении функции. Тогда grad F 1; 2 , построим этот вектор (см. рис. 1).
Проведем линию уровня 1, перпендикулярную вектору градиента. Будем смещать эту линию параллельно самой себе.
Функция будет принимать наименьшее значение в точке «вхо-
да» линии уровня 2 в область допустимых решений в направлении |
||||
градиента. |
Это |
точка |
B 0; 8 . |
Следовательно, |
Fmin F 0; 8 x1 2x2 |
0 2 8 16 . |
|
||
Функция будет принимать наибольшее значение в точке «вы- |
||||
хода» линии уровня 3 из области допустимых решений в направле- |
|||||
нии |
градиента. |
Это |
точка |
D 8; 2 . |
Следовательно, |
Fmax F 8; 2 x1 2x2 8 2 2 4 .
ЗАДАЧА 4. Привести уравнение кривой к каноническому виду и построить линию.
Пример 1.
x2 2 y2 2x 12 y 33 0
Предварительно следует изучит виды кривых 2-го порядка, их уравнения и расположение (табл.1).
Приведём уравнение к каноническому виду. Для членов, содержащих x, и членов, содержащих y, выполним преобразования с выделением полного квадрата:
x2 2x x2 2x 1 1 x 1 2 1;
2 y2 12 y 2 y2 6 y 9 9 2 y 3 2 18.
Данное уравнение теперь можно переписать так:
x 1 2 2 y 3 2 1 18 33 0,
откуда x 1 2 2 y 3 2 |
16 или |
x 1 2 |
|
y 3 2 |
1. |
|
|
16 |
|
8 |
|

|
|
|
|
|
8 |
|
|
|
Это уравнение гиперболы с цен- |
|
y |
|
|||||
тром |
в |
т. O1 1;3 |
и полуосями |
|
|
|||
|
О1 |
|
||||||
|
|
|||||||
a 4, |
b |
|
|
|
|
|
|
|
|
8. |
|
|
|||||
|
|
|
|
|||||
Пример 2. |
|
|
О |
x |
||||
|
|
|||||||
x2 |
4x y2 5 0 |
|
|
|||||
|
|
|
|
|||||
Выпишем слагаемые с x и выделим полный квадрат: x2 4x x2 4x 4 4 x 2 2 4 .
Подставим в исходное уравнение, оставим квадраты слева:
x 2 2 4 y2 5 0 x 2 2 y2 |
9 . |
|
y |
|
|
||
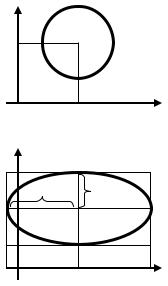
Это уравнение окружности с центром в |
|
|
|
т. 2; 0 и радиусом R 3. |
|
|
|
|
|
|
|
|
|
–2 О 1 x |
|
Пример 3. |
|
|
|
2x y2 8 y 10 0 |
|
|
|
Выпишем слагаемые с y и выделим полный квадрат: y2 8 y y2 8x 16 16 y 4 2 16 .
Подставим в исходное уравнение: |
|
|
|
|
2x y 4 2 16 10 0 . |
y |
|||
Оставим квадрат слева, остальные слагае- |
|
О |
||
|
|
|
3 x |
|
|
|
|
||
мые перенесем вправо: |
|
|
|
|
|
|
|
|
|
y 4 2 2x 6 , |
|
|
|
|
|
–4 |
|||
откуда y 4 2 2 x 3 . Это уравнение |
|
|||
|
|
|
|
|
параболы, вершина в т. 3; 4 , ветви влево.
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
|
|
|
Вид и параметры кривых второго порядка |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Канонические уравнения |
|
|
|
|
|
|
|
|
|
|
|||||||||
Вид |
|
С центром |
|
|
С центром |
|
|
|
|
Параметры |
Изображение |
|
|||||||||||||
(вершиной) |
|
|
(вершиной) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
кривой |
кривой |
|
||||||||||||||||
кривой |
|
|
в начале |
|
|
|
в точке |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
координат |
|
|
x0 ; y0 |
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
5 |
|
|
|
||
Окружность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R – радиус, |
|
|
|||
|
x2 y2 R2 |
|
|
|
|
|
|
|
|
|
|
|
y0 |
R |
|
|
|||||||||
|
x x |
2 |
|
y y |
2 |
|
R |
2 |
x0 |
и y0 – координаты |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
центра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эллипс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
и y0 – координаты |
y |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
центра, |
a |
b |
|
||||
|
|
x |
|
|
y |
|
|
|
|
|
|
|
a – большая полуось, |
y0 |
|
|
|||||||||
|
|
|
|
|
|
1 |
x x0 |
|
|
y y0 |
1 |
|
|
|
|
|
|||||||||
|
|
a |
2 |
|
b |
2 |
a |
2 |
|
|
b |
2 |
|
b – малая полуось |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(если a b ) и |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наоборот (если a b ) |
|
x0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
