
Matematika_7_8_k_r
.pdf
|
|
|
|
|
|
Таблица 3 |
|
|
Общее решение однородного уравнения |
||||
|
|
|
|
|||
Вид общего решения однород- |
|
Корни |
характеристического |
|||
ного уравнения |
|
уравнения |
|
|||
1. |
y0 |
c1ek1x c2ek 2x |
|
k1 ,k 2 |
– вещественные, k1 k 2 |
|
2. |
y0 |
(c1 c2x)ekx |
|
k1 ,k 2 |
– вещественные, k1 k 2 |
|
3. |
y0 |
c1 cos x c2 sin x e x |
|
k1 ,k 2 |
– комплексные, |
|
|
|
|
|
k1 i, |
k 2 i |
|
|
Решение. Общее решение неоднородного уравнения можно |
|||||
записать в виде y y0 Y , где y0 |
– общее решение однородного |
|||||
уравнения |
|
|
|
|||
y 8y 16y 0 ,
которое определяется по табл. 3, а Y – частное решение неоднородного уравнения, которое определяется по табл. 4.
Для определения y0 составим характеристическое уравнение
k 2 8k 16 0 .
Его корни k1 k 2 4 . Следовательно, y0 e 4x (c1 c2x) .
Так как |
правая |
часть уравнения f x 2xe 4x , то |
Y x2 e 4x Ax B . |
|
|
Здесь a 4, |
Pn x 2x, |
r 2 . |
|
Y e 4x Ax3 Bx2 . |
|
Y 4e 4x Ax3 Bx2 e 4x 3Ax2 2Bx |
||
|
e 4x 4Ax3 x2 4B 3A 2Bx . |
|
Y 4e 4x |
4Ax |
3 x2 4B 3A 2Bx e 4x (12Ax2 2x 4B 3A |
2B) e 4x |
16Ax3 x2 16B 24A x 16B 6A 2B . |
|
Подставив эти значения в наше уравнение, получим |
||
e 4x 16Ax3 x2 |
16B 24A x 16B 6A 2B 8e 4x ( 4Ax3 |
|
x2 4B 3A |
2Bx) 16e 4x Ax3 Bx2 2xe 4x . |
|
|
Частное решение неоднородного уравнения |
Таблица 4 |
||||||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Вид правой части |
|
|
Вид частного решения |
|
||||||||
неоднородного дифферен- |
|
|
||||||||||
циального уравнения |
|
|
|
|
|
|
|
|
|
|
||
f x eax Pn x , |
|
y xr eax Qn x , где |
|
|
|
|||||||
Pn x |
– многочлен степени |
0, если a не является корнем |
|
|||||||||
n |
|
|
|
|
характерист. уравнения |
|
||||||
|
|
|
|
|
||||||||
|
|
|
|
1,если a равно одному корню |
|
|||||||
|
|
|
|
r |
характерист. уравнения |
|
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
2, если оба корня характерист. |
|
|||||||
|
|
|
|
|
уравнения равны a |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Qn x - многочлен степени n с не- |
||||||||
|
|
|
|
определёнными коэффициентами |
|
|||||||
|
P x cos bx |
|
y xr eax |
|
S |
|
x cosbx Z |
|
x sinbx |
|
||
f x eax |
n |
|
|
|
|
N |
|
N |
|
|||
|
|
|
|
0, если a bi не является корнем |
||||||||
|
|
Qm x sinbx |
||||||||||
Pn x |
– многочлен степени |
|
характерист. уравнения |
|
||||||||
|
|
|||||||||||
n , |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
1,если a bi равно одному корню |
|||||||||
Qm x |
– многочлен степени |
|
характерист. уравнения |
|
||||||||
|
|
|||||||||||
m |
|
|
|
N равно наибольшей из степеней n |
||||||||
|
|
|
|
и m |
|
|
|
|
|
|
|
|
Сократим на e 4x и сгруппируем члены с x3 , x2 , x, x0 |
|
|
|
|||||||||
|
x3 16A 32A 16A x2 16B 24A 32B 24A 16B |
|
||||||||||
|
x 16B 6A 16B 2B 2x. |
|
|
|
|
|
|
|
|
|||
или |
|
|
6Ax 2B 2x . |
|
|
|
|
|
|
|||
Приравниваем коэффициенты многочленов, стоящих в левой и правой части равенства, при одинаковых степенях x . Получаем систему уравнений для определения A, B .
6A 2, |
|
|
1 |
|
|||
|
A |
|
, |
||||
3 |
|||||||
|
2B |
0. |
|
|
|||
|
|
|
|
|
|||
|
|
|
|
B 0. |
|||
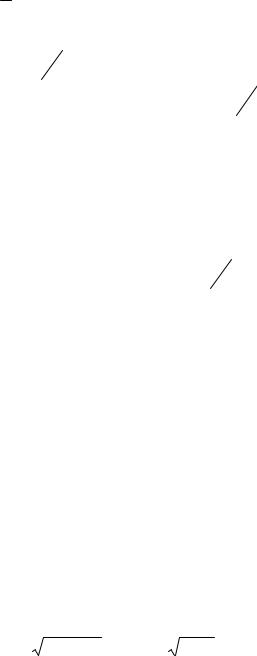
Итак, Y e 4x 1 x3 .
3
Общее решение неоднородного уравнения имеет вид
y e 4x c1 c2x e 4x 1 |
3 |
x3 |
, отсюда |
|
|
|
|||||
y 4e 4x c |
1 |
c |
2 |
x e 4x |
c |
2 |
4e |
4x 1 |
x3 e 4x x2 . |
||
|
|
|
|
|
|
|
3 |
|
|||
Подставляя в эти выражения начальные условия x 0, y 1, y 2 , найдём c1 , c2 .
1 c1 , |
|
c1 1, |
|
|
|
|
|
2 4c1 |
c2 . |
c2 6. |
|
так, искомое решение имеет вид |
|
|
|
y e 4x 1 6x e 4x 1 |
x3 . |
||
|
|
3 |
|
Пример. Найти частное решение дифференциального уравнения
y 6y 13y 4 sin 5x , |
|
удовлетворяющее начальным условиям y 0 0,235; |
y 0 0 . |
Решение. Общее решение неоднородного уравнения можно записать в виде y y0 Y , где y0 – общее решение однородного уравнения
y 6y 13y 0 ,
которое определяется по табл. 3, а Y – частное решение неоднородного уравнения, которое определяется по табл. 4.
Для определения y0 составим характеристическое уравнение
k 2 6k 13 0 .
Его корни k1,2 |
6 |
36 52 |
|
6 |
16 |
|
6 4i |
3 2i . |
|
2 |
|
2 |
2 |
||||
|
|
|
|
|
|
Согласно таблице 3 3, 2 , то есть
y0 e 3x c1 cos 2x c2 sin 2x .
Для определения Y используем табл. 4. Так как f x 4 sin 5x , то a 0, b 5, P0 x 0, Q0 x 4, r 0 . Следовательно,
Y A cos5x B sin 5x .
Для определения A, B подставим Y в первоначальное уравнение

Y 5A sin 5x 5B cos5x , Y 25A cos5x 25B sin 5x .
Тогда уравнение примет вид
25A cos5x 25B sin 5x 6 5A sin 5x 5B cos5x
13 A cos5x B sin 5x 4sin 5x.
Приравнивая коэффициенты при cos5x и sin 5x в левой и правой части этого уравнения, получим систему
12A 30B 0, |
A |
30 |
B |
5 |
B, |
30 |
5 |
B 12B 4, |
B 0,115, |
||
|
|
|
|||||||||
12B |
4. |
12 |
|
|
|||||||
30A |
|
2 |
|
2 |
|
|
|||||
A 5 0,115 0,046. Y 0,115 cos5x 0,046sin 5x .
2
Общее решение нашего уравнения имеет вид
y e 3x c1 cos 2x c2 sin 2x 0,115 cos5x 0,046 sin 5x .
Отсюда
y 3e 3x c1 cos 2x c2 sin 2x e 3x 2c1 sin 2x 2c2 cos 2x
0,575 sin 5x 0,23cos5x.
Найдём из начальных условий y 0 0,235; |
y 0 0 постоянные |
||
c1 , c2 . |
|
|
|
0,235 c1 0,115, |
|
c1 |
0,35, |
|
|
0,64. |
|
0 3c1 2c2 0,23. |
|
c2 |
|
Итак, искомое решение имеет вид
y e 3x 0,35 cos 2x 0,64 sin 2x 0,115 cos5x 0,046 sin 5x .
При решении задач № 91-120 рекомендуется изучить литературу [1, с. 107-109, 111-113; 3, с. 191-193, 199; 4, с. 561-563, 585587; 5, с. 411-420]. Наибольшую трудность представляет составление дифференциальных уравнений, описывающих данную линию.
Задачи решаются с использованием геометрического смысла производной y tg , где – угол наклона касательной к оси OX.
Пусть M(x,y) – точка касания, принадлежащая искомой кривой (рис. 8, 9, 10). OA=x, AM=y, CM – касательная к кривой.
Пример. Кривая обладает тем свойством, что отрезок нормали, заключённой между осями координат и проведённый в любой

точке кривой, делится этой точкой пополам. Записать уравнение кривой, проходящей через точку M0 0,1 .
y
M(x, y)
K
B
C |
O |
A |
x |
|
|
|
|
Рис.8
tg |
AM |
, AC |
AM |
|
y |
|
tg |
y |
|||
|
AC |
|
|||
OC AC x y x, y
OB tg y ,
OC
OB OC y y xy .
y |
|
|
|
B |
|
M(x, y) |
|
|
|
|
|
K |
|
|
|
|
|
|
|
O |
A |
C |
x |
Рис.10
Решение. Пусть M x, y
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M(x, y) |
K |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
O |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
x |
||
|
|
|
C |
|
A |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис.9
AC y , y
OC x AC x y , y
OB tg y ,
OC
OB xy y .
AM tg tg ,
AC
AC y , y
OC x AC x y , y
OB y , OB xy y .
OC
– произвольная точка искомой кри-
вой |
|
(рис. 11). CM – касательная, tg y , |
ED – нормаль, . |
По условию EM MD, |
OA AD, |
OK KE, |
OD 2x, |
OE 2y, |
||||||||
|
OE |
tg , |
2y |
tg ctg |
|
1 |
|
1 |
. |
|
|
|
|
|
|
tg |
|
|
|
||||||
|
OD |
2x |
|
|
y |
|
|
|||||
Получаем дифференциальное уравнение кривой
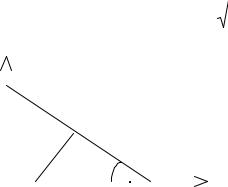
|
y |
|
1 |
, |
y |
x |
, |
dy |
|
x |
, |
ydy xdx, |
|
y2 |
|
|
x2 |
c . |
|||||||||
|
|
|
|
dx |
|
|
2 |
|
|||||||||||||||||||
|
x y |
|
|
|
y |
|
|
y |
|
|
|
2 |
|
|
|||||||||||||
OB – отрезок, отсекаемый касательной на оси oy . |
|
|
|||||||||||||||||||||||||
OC – отрезок, отсекаемый касательной на оси ox . |
|
|
|||||||||||||||||||||||||
OM – радиус-вектор точки касания M, OM |
|
|
. |
||||||||||||||||||||||||
|
x2 y2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
E |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M x, y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
O |
|
C |
|
|
|
A |
|
|
D |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11
Найдём c из условия, что |
линия проходит через точку |
||||
M0 0,1 . |
|
|
|
||
|
1 |
0 c, |
c |
1 |
. |
2 |
|
||||
|
2 |
|
|||
Уравнение искомой кривой имеет вид
y2 |
|
x2 |
|
1 |
или y2 x2 1. |
2 |
|
|
|||
2 |
2 |
|
|||

Контрольная работа №7
Интегралы
1-30. Вычислить неопределённые интегралы
1. |
|
|
|
dx |
|
||||||
a) |
|
|
|
|
, |
|
|
||||
3 |
|
|
|
|
|
||||||
3x 1 |
|
||||||||||
2. |
a) |
|
|
dx |
, |
||||||
x ln2 x |
|||||||||||
3. |
a) |
|
xdx |
, |
|
|
|||||
|
|
|
|
||||||||
|
|
|
|
x4 1 |
|
||||||
4. |
a) |
|
|
dx |
, |
||||||
4x2 7 |
|
||||||||||
5. |
a) |
x cos x2 dx, |
|||||||||
6. |
a) |
|
|
|
cosxdx, |
||||||
|
|
sin x |
|||||||||
b) arccos x dx.
b)
 x 1 dx. x 5
x 1 dx. x 5
b) |
|
ln |
x |
|
dx. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
3 x |
|
|
|
|
||||||||
b) |
|
1 |
|
|
|
|
dx . |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x 3 1 |
|
|
|||||||||
b) |
|
1 x |
|
dx. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
||||||||||
|
|
1 x |
|
|
|
|
||||||||
b) |
|
1 |
|
|
|
dx. |
||||||||
x 12 |
|
|
|
|||||||||||
x 3 |
||||||||||||||
7.a)
8.a)
9.a)
10.a)
11.a)
12.a)
13.a)
14.a)
15.a)
x2 
 x3 5 dx,
x3 5 dx,
2ln x 3 3 dx, x
xdx
4x2 7,
e2xdxe4x 5,
e
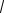 2x 1dx,
2x 1dx, 
 2x 1
2x 1
3
x x2 1 2 dx,
cos sin x cosxdx,
sin xdx
4 cosx

 3 ln 2x dx , x ,
3 ln 2x dx , x ,
b) |
|
x 1 |
|
dx . |
|
|
|
|
|||
1 |
x 1 3 |
||||
|
|
|
b)arcsin x dx.
b)x arctgx dx .
b) |
|
1 |
x |
|
|
|
|
|
dx . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
x 3 |
|
|
x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
b) |
|
1 |
|
|
|
|
|
x 2 |
|
|
dx . |
||||||
x 2 |
|
|
|
|
|
|
|
|
|
||||||||
2 x 2 |
|||||||||||||||||
|
|
|
|
||||||||||||||
|
|
sin2 |
|
|
|
|
|
|
|
|
|
|
|
||||
b) |
|
|
x |
|
dx . |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
 x
x
b)1 
 x 4 dx . x 5
x 4 dx . x 5
b)x 2 ln x dx .
b)x2 arcsin x dx .
16.a)
17.a)
18.a)
19.a)
20.a)
21.a)
22.a)
23.a)
24.a)
25.a)
26.a)
27.a)
28.a)
29.a)
30.a)
2
x ex 3dx,
2dx
4x x ln x, dx
|
|
|
|
|
|
|
|
|
|
, |
|
1 cos6x |
|||||||||||
|
sin 2x dx |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
1 cos 2x |
|
|
||||||||
|
|
x2dx |
|
|
|||||||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
||||||||
|
|
x3 5 |
|
|
|||||||
|
|
|
4dx |
|
|
||||||
|
|
|
|
|
|
|
, |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
||||||||
|
|
2 6x2 |
|
|
|||||||
|
cosx dx |
, |
|
|
|||||||
|
|
|
|
|
|||||||
3 sin2 x |
|
|
|||||||||
|
|
|
|||||||||
x e x 2 dx,
sin 
 x dx,
x dx,
|
|
|
x |
|
|
|
|
|
|||
|
x |
2dx |
|
|
|
|
|
||||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
|
|
|
|
|
|
|
|||
|
|
6 1 |
|
|
|
|
|
||||
|
cosx dx |
|
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
3 3 5 sin x |
|
|
|
||||||||
|
|
|
|
|
|
||||||
|
|
dx |
|
|
|
|
|
||||
|
|
, |
|
|
|
|
|
||||
x ln3 x |
|
|
|
|
|
||||||
|
|
|
|
|
|
dx |
|
|
|
|
, |
arccosx 5 |
|
|
|
|
|||||||
|
|
|
|||||||||
|
|
1 x2 |
|||||||||
dx
arctg3x 1 x2 ,

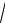 arcsin3 x dx ,
arcsin3 x dx ,
 1 x2
1 x2
b)arctg
 x dx .
x dx .
b)x2 e3x dx.
b) |
|
|
x |
dx . |
|
||||||
|
|
|
|||||||||
|
|
sin2 x |
|
|
|
|
|||||
b) |
|
x sin x |
dx . |
||||||||
|
|
|
|
||||||||
|
|
cos2 x |
|
|
|
|
|||||
b) |
|
|
4 x |
|
|
|
dx . |
||||
|
|
|
|
|
|
|
|
|
|||
|
x 1 7 |
||||||||||
|
|
|
|
||||||||
|
|
|
|
|
dx . |
||||||
b) |
|
|
x 2 |
||||||||
|
|
|
|
||||||||
|
|
x 11 |
|
|
|
|
|||||
b) |
|
1 |
|
|
|
|
dx . |
||||
|
|
|
|
|
|
|
|||||
|
3 ex |
||||||||||
|
|
|
|
|
|
|
|||||
b)ln2 x dx . x2
e3x
b) dx .
dx .
 1 ex
1 ex
b)x2 e 2x dx .
b) |
|
1 x |
2 |
|
dx . |
ln x |
|
|
|||
|
|
|
|
|
|
b)x2 cosx dx .
b)
 x ln2 x dx .
x ln2 x dx .
x2
b)  dx .
dx .  x 1
x 1
b) x2 sin 2x dx .
31-60. Задачи на геометрические приложения определённого интеграла

31. Найти площади частей, на которые круг x2 y2 8 делится
параболой y 1 x2 .
2
32. Найти площадь фигуры, ограниченной линией y x x 1 2 и
осью абсцисс Ox .
33. Найти длину дуги параболы y x2 от точки x 0 до точки
x1 .
34.Найти объём тела, образованного вращением вокруг оси Ox
фигуры, ограниченной линиями y 1 x2 и 2x 2y 3 0 .
2
35. Найти объём тела, образованного вращением вокруг оси Ox фигуры, ограниченной линиями y 0 и y sin2 x, 0 x .
36.Найти площадь фигуры, ограниченной параболами x2 8y 8
иx2 24y 40 .
37.Найти площадь фигуры, ограниченной линией y ln x и пря-
мыми x e, |
x e2 , |
y 0 . |
|
|
|
|
|
||||
38. |
Найти длину дуги кривой y |
1 |
3 x |
|
между точками её пе- |
||||||
x |
|||||||||||
|
|||||||||||
|
|
|
3 |
|
|
|
|
|
|
||
ресечения с осью Ox . |
|
|
|
|
|
||||||
39. |
Вычислить объём тела, образованного вращением вокруг оси |
||||||||||
Ox фигуры, ограниченной линиями y |
|
|
, y 0, |
x 1. |
|||||||
|
4x |
||||||||||
40. |
Найти длину дуги кривой y ln x от |
точки x |
|
до точки |
|||||||
3 |
|||||||||||
x 
 8 .
8 .
41. Вычислить площадь криволинейной трапеции, ограниченной
|
|
|
3 |
|
|
|
|
линией y x x |
2 |
и осью абсцисс Ox . |
|
|
|||
42. |
Найти объём тела, образованного вращением вокруг оси Ox |
||||||
фигуры, ограниченной линиями y x ex , |
x 1, |
y 0 . |
|||||
43. |
Найти площади фигур, на которые парабола y2 6x делит |
||||||
круг x2 y2 16 . |
|
|
|||||
44. |
Вычислить площадь фигуры, заключённой |
между линией |
|||||
y |
1 |
и параболой y 0,5x2 . |
|
|
|||
1 x2 |
|
|
|||||
|
|
|
|
|
|
|
|

45. Найти объём тела, образованного вращением вокруг оси Oy
фигуры, ограниченной линиями y 0,5 x 2 2 и y 2 .
46. |
Найти длину дуги кривой x |
1 |
t6 , |
y 4 |
1 |
t4 между точками |
||
|
|
|||||||
|
6 |
|
|
4 |
|
|
||
её пересечения с осями координат. |
|
|
|
|
|
|||
47. |
Найти объём тела, образованного вращением вокруг оси Ox |
|||||||
фигуры, ограниченной линиями y e2x 1, |
y e x 1, |
x 0 . |
||||||
48. |
Найти длину дуги кривой y ln 1 x2 от точки x 0 до точки |
|||||||
x 0,5 . |
|
|
|
|
|
|||
49. |
Вычислить площадь фигуры, ограниченной линиями y ln x и |
|||||||
yln2 x .
50.Найти площадь фигуры, ограниченной линией y arcsin x и
прямыми x 0, |
y |
|
. |
|
|
|
|
|
|||
|
2 |
|
|
|
|
51. Найти длину дуги кривой x et cos t, |
y et sin t от |
t 0 до |
|||
точки t 1. |
|
|
|
|
|
52.Найти объём тела, образованного вращением параболического сегмента с основанием 2a и высотой h вокруг высоты.
53.Вычислить площадь фигуры, ограниченной линиями y2 x 1
иy2 9 x .
54. |
Вычислить |
|
площадь |
фигуры, |
ограниченной |
|
линиями |
|||||||||||||
y sin x, |
y cosx, |
y 0, |
x 0, |
x |
|
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
55. |
Найти длину дуги астроиды x a cos3 t, |
y a sin3 t, |
|
0 t |
. |
|||||||||||||||
|
|
|||||||||||||||||||
|
Найти длину дуги полукубической параболы y2 x3 |
2 |
|
|||||||||||||||||
56. |
от нача- |
|||||||||||||||||||
ла координат до точки M 4,8 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
57. |
Фигура ограничена кривой |
x a cos t, |
y a sin t, |
0 t |
|
и |
||||||||||||||
|
||||||||||||||||||||
осями координат Ox, Oy Найти объём тела вращения. |
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||
58. |
Вычислить |
|
площадь |
фигуры, |
ограниченной |
|
линиями |
|||||||||||||
y 2 |
|
, |
y |
|
3 и осью Oy . |
|
|
|
|
|
|
|
|
|
|
|
||||
x |
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||
59. |
Вычислить |
|
площадь |
фигуры, |
ограниченной |
|
кривыми |
|||||||||||||
y ex 1, |
y e2x 3, |
x 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
