Физическая химия Часть 1 учебное пособие

100

В предельно разбавленных растворах для определения парциального давления пара растворенного вещества применяется закон Генри

Выражение (2.2.29) называется законом или уравнением Генри. Парциальное давление пара растворенного вещества над предельно разбавленным раствором пропорционально молярной доле

растворенного вещества в этом растворе.

Для идеальных растворов K2 = p20 и уравнение Генри прини-

мает вид уравнения Рауля.

Неидеальные растворы.

Для растворителя и растворенного вещества используют соответственно

Если оба компонента – взаимно растворимые жидкости, то за стандартное состояние выбирают чистое вещество. При этом уравнения для давления пара над раствором имеют вид

2.2.4. Общее давление пара над идеальным раствором

Общее давление пара над идеальным раствором равно сумме парциальных давлений пара отдельных компонентов.

101

Используем закон Рауля

p = p10x1 + p20x2 = p10 (1− x2 )+ p20x2 == p10 − p10x2 + p20x2,

выносим x2 :

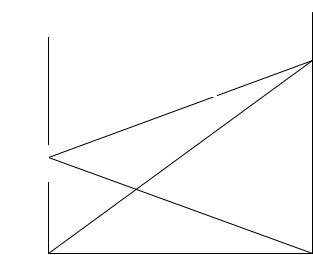
Парциальные давления пара растворителя и растворенного вещества (2.2.33), а также общее давление пара над раствором (2.2.34) линейно зависят от состава раствора. Зависимость общего давления пара и парциальных давлений паров отдельных компонентов от состава представлена на рис. 2.5. Линии парциальных давлений компонентов выходят их начала координат и оканчиваются

в точках p10 и p20 , отвечающих давлению пара соответствующего

чистого компонента. Эти точки соединяются линией общего давления. На рисунке представлен случай, когда второй компонент явля-

ется более летучим p20 > p10 . В этом случае с увеличением молярной доли второго компонента общее давление пара раствора увели-

раствора. Если растворенное вещество нелетучее, то общее давление пара практически равно давлению пара растворителя.

102

p

p20

P=f(x2)

p2

p10

p1

Рис. 2.5. Зависимость общего давления пара и парциальных давлений паров компонентов от состава

раствора

2.2.5. Температура замерзания раствора

Раствор, в котором растворенное вещество является нелетучим, замерзает при более низкой температуре, чем чистый растворитель. Чистый растворитель или раствор замерзает при той температуре, при которой давление пара растворителя над чистым жидким растворителем или над раствором будет равно давлению пара над чистым твердым растворителем.

Условие замерзания чистого растворителя выражается уравне-

нием

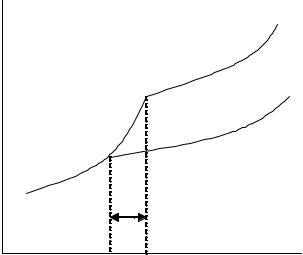
Зависимость давления пара растворителя над твердым (p1,0 тв)

и жидким (p1,0 ж ) чистым растворителем и над раствором (p1 ) от температуры показана на рис. 2.6.

p1

p10, тв

Рис. 2.6. Зависимость давления пара растворителя над твердым и жидким растворителем и над раствором от температуры

Используя условия (2.2.35) и (2.2.36), определяем температуры замерзания чистого растворителя Тз0 и раствора Тз. Температура замерзания раствора Тз ниже, чем температура замерзания чистого

растворителя Тз0 . Это связано с тем, что, в соответствии с законом

Рауля, давление пара над раствором нелетучего вещества меньше, чем давление пара над чистым растворителем. Разность

∆Tз =Тз0 −Тз называется понижением температуры замерзания

раствора. Для предельно разбавленных растворов для расчета понижения температуры замерзания раствора используют выражение

где Kз – криоскопическая постоянная, рассчитывается по уравнению

Криоскопическая постоянная численно равна понижению температуры замерзания раствора с моляльной концентрацией

104

т = 1 моль/кг. Криоскопическая постоянная зависит от свойств растворителя и не зависит от природы растворенного вещества.

Из уравнения (2.2.37) можно определить молекулярную массу растворенного вещества по опытным данным.

2.2.6. Температура кипения раствора

Раствор закипает при более высокой температуре, чем чистый растворитель. Чистый растворитель или раствор начнет кипеть при такой температуре, при которой давление пара растворителя над чистым растворителем или над раствором будет равно внешнему давлению р (в обычных условиях р = 1 атм = 1,0133·105 Па). Растворенное вещество будем считать нелетучим.

Условие кипения растворителя

Из закона Рауля следует, что давление пара растворителя над идеальным раствором меньше, чем над чистым растворителем при той же температуре:

p = p1 = p10 x1 = p10 (1 − x2 ),

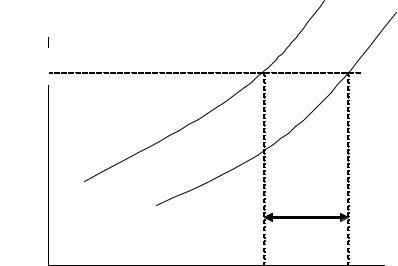
чем больше x2 , тем меньше р. Зависимость давления пара раство-

рителя от температуры над чистым растворителем и над раствором показана на рис. 2.7. Температура кипения идеального раствора Тк

выше, чем температура кипения чистого растворителя Тк0 , это свя-

зано с понижением давления пара над раствором по сравнению с чистым растворителем.

Разность ∆Т =Тк −Тк0 называется повышением температуры

кипения раствора. Повышение температуры кипения предельно разбавленного раствора рассчитывают по уравнению

Эбулиоскопическая постоянная растворителя Kк определяется выражением

Эбулиоскопическая постоянная численно равна повышению температуры кипения раствора с моляльной концентрацией т = 1 моль/1000. Эбулиоскопическая постоянная растворителя не зависит от природы растворенного вещества, а зависит от свойств растворителя.

Из уравнения (2.2.42) можно определить молекулярную массу растворенного вещества по опытным данным.

106

2.2.7. Осмотическое давление

При погружении в воду стеклянной трубки, закрытой с одного конца полупроницаемой перегородкой и заполненной водным раствором сахара, в трубке происходит увеличение объема раствора за счет проникновения воды через полупроницаемую перегородку.

Осмос – это самопроизвольное проникновение молекул растворителя в раствор, отделенный от него полупроницаемой перегородкой, через которую может поступать растворитель, но не может проходить растворенное вещество. Осмотическое давление π равно избыточному внешнему давлению, которое нужно приложить к раствору, чтобы прекратился осмос, и в системе установилось равновесие.

Полупроницаемые перегородки могут быть природными (ткань, отделяющая клетки живых организмов, плавательный пузырь рыбы) и искусственными (целлофан, минеральные коллоидные осадки, различные ВМС).

Вант – Гофф показал, что осмотическое давление разбавленных растворов подчиняется уравнению

Уравнение Вант – Гоффа можно получить из термодинамических соображений.

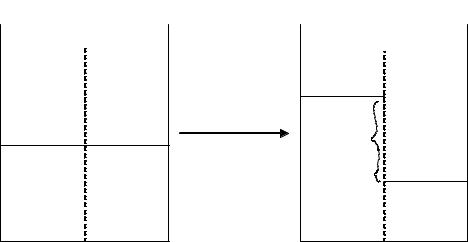
На рис. 2.8 схематически изображен процесс осмоса.

Раствор и растворитель, разделенные полупроницаемой перегородкой, можно рассматривать как две фазы I и II. Переход растворителя через полупроницаемую перегородку обусловлен с точки зрения термодинамики различием химических потенциалов чистого

растворителя µ1•(II ) и растворителя в растворе µ1(I ). Растворитель

будет проникать в раствор через полупроницаемую перегородку до тех пор, пока в системе не установится равновесие. При равновесии

107

химический потенциал растворителя в растворе, к которому приложено дополнительное давление π, равен химическому потенциалу

чистого растворителя µ1(I ) = µ1•(II ).

Осмотическое давление предельно разбавленного раствора определяется уравнением Вант – Гоффа

где с – молярная концентрация.

Из сравнения уравнения Вант – Гоффа с уравнением Менделеева – Клапейрона следует, что осмотическое давление разбавленного раствора равно тому давлению, которое бы оказывало растворенное вещество на стенки сосуда, если бы оно в виде идеального газа при той же температуре занимало объем, равный объему раствора.

Рис. 2.8. Схематическое изображение процесса осмоса

Осмотическое давление проявляется только на границе между раствором и растворителем, граница – полупроницаемая перегородка.

Осмотическое давление имеет очень большое значение в процессах жизнедеятельности различных организмов, определяя рас-

108

пределение растворенных веществ и воды в тканях. Осмотическое давление крови у человека составляет примерно 8,1·105 Па.

2.2.8. Теплоты растворения

Изменение энтальпии при переходе твердого, жидкого или газообразного вещества в раствор называют теплотой или энтальпией растворения. Различают интегральные и дифференциальные теплоты растворения.

Интегральной теплотой растворения называют изменение энтальпии при растворении 1 моля вещества в некотором количестве чистого растворителя. Интегральные теплоты растворения зависят от концентрации полученного раствора и от температуры. Так как можно получить растворы разной концентрации, то число интегральных теплот растворения может быть сколь угодно большим. Особый интерес представляют первая и полная интегральные теплоты растворения.

Дифференциальной или парциальной теплотой растворения

называется изменение энтальпии при растворении 1 моля вещества в бесконечно большом количестве раствора данной концентрации. В этом процессе концентрация раствора остается неизменной или, точнее, возрастает на бесконечно малую величину, которой можно пренебречь.

2.2.9. Растворимость твердых веществ в жидкостях

Растворимость измеряется концентрацией растворенного вещества в растворе, которое находится в равновесии с этим веществом в твердой фазе.

Растворимость твердых веществ в жидкостях зависит от природы растворяемого вещества и растворителя, температуры, давления и присутствия в растворе посторонних веществ, особенно электролитов. Полярные вещества лучше растворяются в полярных растворителях, а неполярные вещества лучше растворяются в неполярных растворителях.

Зависимость растворимости твердых тел в жидкостях от давления проявляется при высоких давлениях (порядка 108 Па), а при небольших давлениях практически не проявляется.

так как производная имеет отрицательное значение. Разница в числителе невелика, поэтому влияние давления незначительно.

Растворимость твердых веществ в жидкостях зависит от температуры. Количественно зависимость растворимости твердых веществ в жидкости от температуры выражается уравнением Шредера

плавления второго компонента.

Если теплота плавления растворенного вещества имеет положительное значение, то с ростом температуры растворимость твердых тел в жидкости увеличивается, если отрицательное – уменьшается, если равна нулю – растворимость не зависит от температуры.

Разделяем переменные и интегрируем уравнение (5.47), считая

∆Нплo ,2 = const:

Из уравнения следует, что растворимость твердого тела в идеальном растворе не зависит от природы растворителя, раствори-