Физическая химия Обучающая программа

41

Задание 5

В задании 5 рассмотрено решение задач по термодинамической теории растворов.

Расчеты провести для раствора неизвестного нелетучего вещества (табл. 2) в жидком растворителе A с концентрацией c (масс.%) и плотностью d (кг/м3) при температуре T и давлении

P1 (Па).

Таблица 2

Продолжение таблицы 2

Расчеты проведены для 16 варианта, его студенты не реша-

ют.

где p1 / p10 – относительное понижение давления пара растворителя над раствором, x2 – молярная доля растворенного вещества.

x2 87711 84990 0,031. 87711

5.2. Рассчитайте молярную массу растворенного вещества. Из уравнения молярной доли

x2 n2n2 n1 ,

и количества молей вещества

ni gi ,

Mi

где gi – вес вещества; Mi – молярная масса,

получим уравнение для расчета молярной массы растворенного вещества

g2

x2 g2M2 g1 .

M2 M1

43

Так как массовая концентрация раствора c, мас.% 5, то g2 5г, а g1 95г. В табл. 2 находим молярную массу раствори-

теля M1 83,5г/ моль. Величину x2 берем из п. 5.1.

5.3. Определите молярную концентрацию раствора. Молярная концентрация – это количество молей вещества в

единице объема (1 дм3, 1 м3): c nV2 , мольдм3 . Если неизвестно ко-

личество раствора, а известен только массовый процент, то удобно брать массу раствора 100 г. Объем раствора определяем по уравнению

V dg .

Плотность раствора рассчитываем в граммах на кубический сантиметр (г/см3):

d 2160 кг/ м3 2160000 г/106 см3 2,16 г/ см3 .

V 2,16100 46,3 см3.

Составляем пропорцию:

5г 46,3см3 x 1000см3

44

Находим количество граммов вещества, содержащиеся в объеме 1000 см3 (1 дм3):

x 5 1000 107,99 г. 46,3

Рассчитываем количество молей растворенного вещества в

1000 см3 (1 дм3):

n2 g2 107,99 0,78 моль. M2 138,6

Так как это количество молей вещества растворено в 1 дм3, то молярная концентрация равна

c nV2 0,781 0,78 моль/ дм3.

Можно провести расчет иначе:

V 2,16100 46,3см3 0,0463дм3 ,

n2 138,65 0,0361моль,

c nV2 0,04670,0361 0,78 мольдм3 .

5.4. Определите моляльную концентрацию раствора. Моляльная концентрация раствора – это количество молей

вещества в 1000 г (1 кг) растворителя.

В 100 г данного раствора содержится 5 г растворенного вещества, количество растворителя 100 5 95г. Составляем пропорцию

Количество граммов растворенного вещества в 1000 г растворителя определяем из пропорции:

x 5 100095 52,63г.

Рассчитываем количество молей вещества в 1000 г растворителя:

n 138,652,63 0,38 моль.

Так как это количество молей растворено в 1000 г растворителя, то моляльная концентрация равна

m 0,38моль/1000 0,38 моль/ кг.

Можно провести расчет по формуле

m g2 1000 ,

M2 g1

Можно провести расчет по уравнению, где g1 кг.

5.5. Вычислите осмотическое давление раствора. Осмотическое давление раствора рассчитываем по уравне-

нию Вант-Гоффа

46

сRT ,

где молярная концентрация имеет размерность с моль/ м3.

Переведем концентрацию из размерности моль на кубический дециметр (моль/дм3) в размерность моль на кубический метр (моль/ м3):

с 0,78 моль/ дм3 780 моль/ м3 .

Рассчитываем осмотическое давление раствора в паскалях

(Па):

780 8,31 119,6 775223,3 Па.

Значение осмотического давления можно перевести в атмосферы:

775223,3:1,013 105 7,65атм.

Можно сразу рассчитать осмотическое давление в атмосферах, если использовать значение газовой постоянной

с 0,78 мольдм3 :

0,78 0,082 119,6 7,65атм.

5.6.Определите молярную долю растворителя в растворе. Рассчитайте значение давления пара растворителя P1, используя

значения Р1(0 ж) при всех температурах (табл. 2 задание 4). Молярная доля растворителя в растворе:

x1 1 x2 1 0,031 0,969

Парциальное давление пара растворителя над раствором определяем по закону Рауля:

47

p1 p10 x1.

Равновесное парциальное давление пара компонента в идеальном растворе пропорционально молярной доле этого компонента в растворе.

Данные заносим в таблицу 3.

Tаблица 3

5.7. Постройте кривую зависимости p f T для данного

раствора. Для растворов нелетучих веществ можно принять, что давление пара над раствором равно парциальному давлению пара растворителя p1 p .

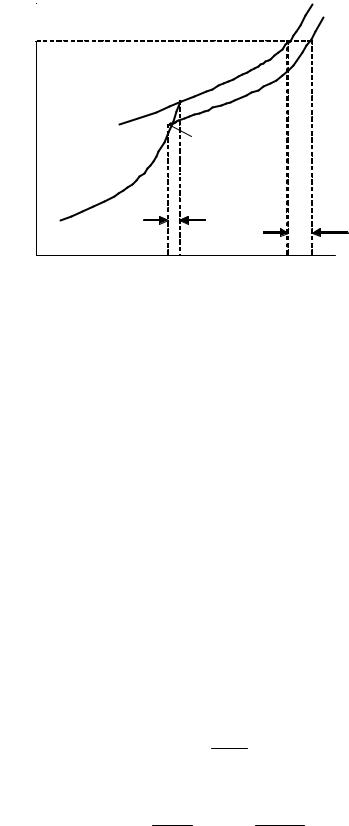
Кривая зависимости p1 p f T построена поданным табл. 3 и представлена на рис. 5.1.

5.8. Определите графически повышение температуры кипения при давлении P1 раствора данной концентрации c .

Для графического определения повышения температуры кипения раствора (рис. 5.1) проводим линию из точки на оси ординат P1 84996 Па, параллельно оси абсцисс (так как нужно

найти температуры кипения жидкостей при этом давлении). Из точек пересечения этой изобары с кривыми испарения чистого растворителя и раствора опускаем перпендикуляры на ось абс-

цисс. Определяем температуры кипения чистого растворителя Тк0 и раствора Tк .

5.9. Вычислите эбулиоскопическую постоянную из полученного в п. 5.8 значения Tк и по теоретическому уравнению,

сравните эти величины между собой. Используем уравнение

Тк Kкm .

Выражаем эбулиоскопическую постоянную из уравнения и рассчитываем, используя значение Tк 1,1K :

Kк mTк .

Kк 0,381,1 2,89 Kмолькг .

Теоретическое уравнение для расчета эбулиоскопической постоянной

49

Значение теплоты испарения берем из 4 задания, п. 4.3.

Hисп 6648 Дж/ моль

Kк 8,31 118,52 83,5 1,46 K кг . 6648 1000 моль

Полученные величины отличаются в два раза.

5.10. Определите графически понижение температуры замерзания раствора.

Для графического определения понижения температуры замерзания используем рис. 5.1 и условия замерзания жидкости.

Условие замерзания чистого растворителя

p10,ж p10,тв

выполняется в точке O .

Условие замерзания раствора нелетучего вещества

p p1,ж p1,0тв

выполняется в точке L . Из этих точек опускаем перпендикуляры на ось абсцисс и определяем температуру замерзания чистого

растворителя Tз0 и температуру замерзания раствора Tз.

По уравнению Tз Тз0 Тз рассчитываем понижение температуры замерзания раствора:

Tз 115,5 114,2 1,3K

50

5.11. Вычислите криоскопическую постоянную из полученного в п. 5.10 значения Tз и по теоретическому уравнению,

сравните эти величины между собой. Используем уравнение

Тз Кзт.

Выражаем криоскопическую постоянную и рассчитываем, используя значение Tз 1,3K :

Kз mTз ,

Kз 0,381,3 3,42 Kмолькг .

Теоретическое уравнение для расчета криоскопической постоянной

Значение теплоты плавления берем из 4 задания п. 4.5.

Hпл 3280,8 Дж/ моль;

Kк 8,31 115,52 83,5 2,82 K кг. 3280,8 1000 моль

Полученные величины отличаются незначительно.

Задание 6

В задании 6 рассмотрено решение задач по теории растворов электролитов.