2. Метод разностных уравнений

Построение кривых переходного процесса на основе разностных уравнений требует:

• получения разностного уравнения на основе заданного дифференциального уравнения;

• выбора шага дискретизации Dt для обеспечения требуемой точности.

Разностные уравнения получаются путем замены в дифференциальных уравнениях дифференциалов левыми разностями на основе выражений:

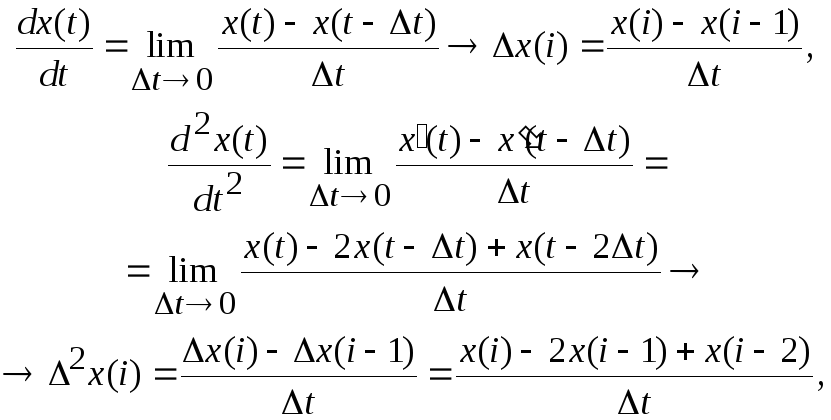(2.16)

где Dt – шаг дискретизации;

i – аналог дискретного времени, представляющий собой целочисленное значение, характеризующее номер дискретного времени t_i = i Dt при равномерной дискретизации.

Линейное разностное уравнение n-го порядка обычно записывается в виде рекуррентной формулы вида

(2.17)

где и– коэффициенты разностного уравнения, определяемые через коэффициенты дифференциального уравнения и шаг дискретизацииDt;

y(i), y(i - 1), …, y(i - n) – значения выходной переменной системы;

v(i), v(i - 1), …, v(i - m) – значения входной переменной системы.

Кривая переходного процесса по разностному уравнению строится следующим образом:

1. Получается разностное уравнение на основе заданного дифференциального уравнения.

2. Задается начальный шаг дискретизации Dt₀. При этом ориентируются на значения постоянных времени T₁, T₂, ..., T_n. Зачастую Dt₀ принимается равной 0,5T_min.

3. Формируются дискретные значения входного воздействия путем дискретизации его известного аналогового выражения, то есть

, (2.18)

где i = 0, 1, 2, 3, ....

4. Рассчитываются значения кривой переходного процесса по полученному разностному уравнению с учетом дискретных значений входного воздействия.

5. Оценивается точность аппроксимации при выбранном шаге дискретизации Dt₀. При этом кривая переходного процесса y(t) заменяется отрезками прямых линий (рисунок 2.7). Точность аппроксимации определяется по выражению

, (2.19)

где j – номер итерации (этапа) выбора шага дискретизации;

n_j – число значений кривой переходного процесса, рассчитываемых по разностному уравнению, которое зависит как от величины шага дискретизации, так и от длительности переходного процесса.

При начальном шаге дискретизации определяется величина E(0).

Изменяется шаг дискретизации (обычно в меньшую сторону) в зависимости от типа переходного процесса и значений параметров на величину (0,1¸0,5)Dt₀ и повторяются этапы 3 – 5. И так до тех пор, пока шаг дискретизации не будет удовлетворять условию

. (2.20)

Рисунок 2.7 – Схема расчета ошибки аппроксимации

При этом необходимо учитывать, что с уменьшением Dt увеличивается число рассчитываемых значений кривой переходного процесса. Если на первой итерации оказалось, что относительная ошибка аппроксимации (2.20) намного меньше 5%, то Dt можно наоборот увеличить.

6. Строится результирующая кривая переходного процесса для выбранного шага дискретизации.

3. Примеры расчета оценок качества регулирования и построения кривых переходного процесса

   1. Определение коэффициентов ошибок

Структурная схема САР приведена на рисунке 3.1, где

. (3.1)

Рисунок 3.1 – Структурная схема САР

Требуется определить:

• коэффициенты статической ошибки C₀, скоростной ошибки C₁ и ошибки от ускорения C₂.

Для нахождения указанных коэффициентов необходимо найти передаточную функцию ошибки по выражению (2.3), то есть

.

Итак

,

на основе выражений (2.4) имеем, что

Для нахождения C₁ необходимо найти первую производную от W_(p) по правилу:

, (3.2)

где B(p) – полином в числителе передаточной функции;

A(p) – полином в знаменателе.

Тогда

Итак

. (3.3)

Тогда

.

Вторая производная от передаточной функции ошибки

Отсюда

.

Итак

C₀ = 0,09; C₁ = 0,25; C₂ = 0,69.

Тогда

.