2.2.2 Группа звеньев 2 – 3

Изображаем группу звеньев 2 – 3 в масштабе μ_L=0,002 м/мм.

Рассмотрим силы, действующие на группу звеньев 2 – 3.

В центре тяжести звеньев S₂ и S₃ приложены силы веса G₂, G₃, направлены вертикально вниз.

Силу инерции прикладываем в точке Т₂ и направляем противоположно вектору ускорения центра тяжести звена 2. Точку Т₂ находим, откладывая от направления линии действия силы инерции приложенной в центре тяжести S₂, плечо h₂ таким образом, чтобы сила инерции , приложенная в точке Т₂, создавала момент относительно S₂ того же направления, что и момент .

Силу инерции P_И3 прикладываем в точке В и направляем противоположно вектору ускорения центра тяжести звена 2.

Сила направлена в сторону скорости точку В.

Освобожденные связи заменяем реакциями.

В шарнире А со стороны звена 1 действуют реакции связи. Обозначим её R₁₂. Она не известна ни по величине, ни по направлению. Для упрощения решения задачи разложим эту реакцию на две составляющие: нормальную направленную вдоль линииAB звена 2, и касательную , направленную перпендикулярно линииAB звена 2.

Под действием всех внешних сил, сил инерции и реакций связей структурная группа находится в равновесии. Исходя из условий равновесия, составим уравнение моментов всех сил, действующих на группу, относительно точки В (при этом для звена 2) и определим касательную составляющую силы.

Будем считать моменты, действующие против часовой стрелки, положительными, а по часовой – отрицательными. Плечи сил определяются непосредственным замером на чертеже в миллиметрах и обозначаются буквой h с индексом соответствующей силы.

Исходя из условия равновесия звена 2 запишем:

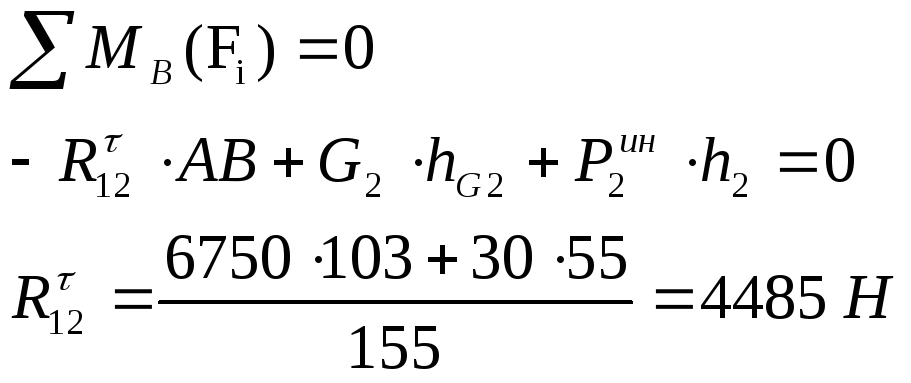
Составим векторное уравнение равновесия сил, действующих на группу 2 – 3 ().

Полученное векторное уравнение имеет два неизвестных и может быть легко решено графическим методом, путем построения многоугольника сил. Равенство говорит о том, что этот многоугольник сил должен быть замкнутым.

Построение плана сил начинаем с линии действия реакции ,на ней в произвольном месте намечаем точку, из которой последовательно одна за другой откладываем в масштабе все силы:

Принимаем масштабный коэффициент плана сил равным

μ_Р=500 Н/мм.

Тогда масштабные (на чертеже) отрезки сил в миллиметрах определятся как частное от деления абсолютной величины силы на масштабный коэффициент, значения сил в миллиметрах пишем в уравнении под значениями в Ньютонах

Затем строим по порядку силы, геометрически складывая и действия реакции. Из конца построения проводим линию действия реакции до пересечения с линией

.

Определим реакцию в шарнире B – R₂₃. Для этого рассмотрим условие равновесия третьего звена:

При помощи плана сил =112мм,=56000Н

2.2.3 Силовой расчёт входного звена механизма

Вычерчиваем входное звено 1 в масштабе μ_L=0,002 м/мм с соблюдением заданного положения, показав все действующие силы. Рассмотрим эти силы. В точке А на звено 1 со стороны звена 2 действует сила(приведённая сила), равная по величине, но противоположная по направлению. Также в точке А на звено 1 со стороны звена 4 действует сила(приведённая сила), равная по величине, но противоположная по направлению.

Силы ибыли определены из планов сил групп 2 – 3 и 4 – 5 равны по абсолютной величине:

Сила инерции =0, так как центр тяжести звена 1 – точка S₁ лежит на оси вращения звена 1 (точка О).

Силой веса звена 1 G₁ пренебрегаем.

Момент от силы инерции =0, так как ε₁=0.

Под действием реакций извено 1 в равновесии не находится. Найдём уравновешивающую силуиз условия равновесия входного звена.

Исходя из условия равновесия входного звена, запишем:

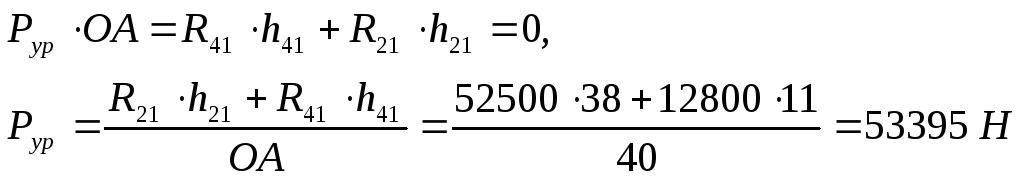
Для определения реакции в шарнире О - , составляем векторное уравнение равновесия сил, действующих на входное звено 1:

Строим план сил входного звена в масштабе:

μ_Р=1000 Н/мм.

Из полученного плана сил видим что вектор изображает в масштабе реакцию R₆₁. Определим величину реакции R₆₁: