Karmazin_-_Teoria_Igr_Uchebnik / P1_3

Тема 1. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО

ПРОГРАММИРОВАНИЯ

Графический метод применяется для решения задачи линейного программирования в стандартной форме с двумя переменными:

найти решение 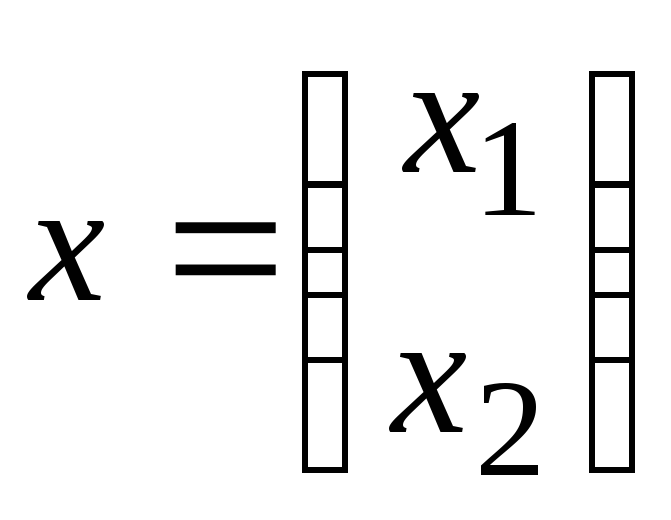, доставляющее

(1)

при ограничениях:

(2)

. (3)

Такие задачи допускают наглядную геометрическую интерпретацию. Каждое из неравенств (2) определяет на координатной плоскости некоторую полуплоскость, а система всех неравенств (2) и (3) в случае их совместности  выпуклый многоугольник.

Пример 1. Решить задачу линейного программирования:

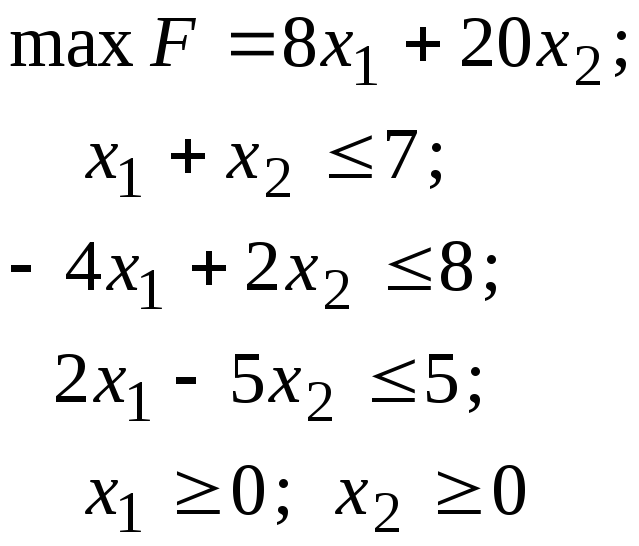(4)

графическим способом.

Сначала построим область допустимых решений. Множество решений, удовлетворяющих условиям и , представляет собой первую четверть координатной плоскости . Множество точек удовлетворяющих условию , есть полуплоскость, границей которой является прямая . Чтобы определить полуплоскость, в которой выполняется данное неравенство, достаточно взять произвольную точку, через которую не проходит граничная прямая. Если пробная точка удовлетворяет ограничению-неравенству, то это неравенство выполняется в полуплоскости, содержащей пробную точку. В противном случае берется полуплоскость, не содержащая пробной точки. В данном случае, возьмем точку в качестве пробной.

На рис. 1 выделена область, полученная пересечением полуплоскостей, соответствующих неравенствам .

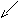
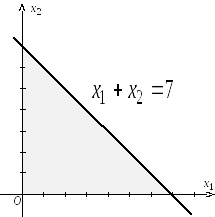
Рис. 1

Далее строим прямые и (рис. 2) и с помощью пробной точки O (0,0) находим полуплоскости соответствующие неравенствам и . Затем определяем множество допустимых решений, являющееся пересечением полуплоскостей всех ограничений неравенств  это будет многоугольник .

Найдем среди множества точек из области допустимых решений такие, которые придают заданной целевой функции наибольшее значение. Рассмотрим линию уровня линейной функции , т.е. линию, вдоль которой эта функция принимает одно и то же фиксированное значение. Линия уровня линейной функции представляет собой прямую. Линия уровня является прямой . Все остальные линии уровня будут параллельны этой прямой. Можно легко убедится, что если эту прямую передвигать параллельно самой себе в направлении вектора нормали , то целевая функция будет возрастать, а в противоположном направлении убывать.

Поэтому наибольшее значение целевая функция нашего примера примет в вершине B многоугольника множества допустимых решений. Вершина B является точкой пересечения прямых и , найдем ее координаты , решив систему линейных уравнений

Целевая функция примет в этой точке максимальное значение .

Задание. В задачах 1.1  1.104 для заданных

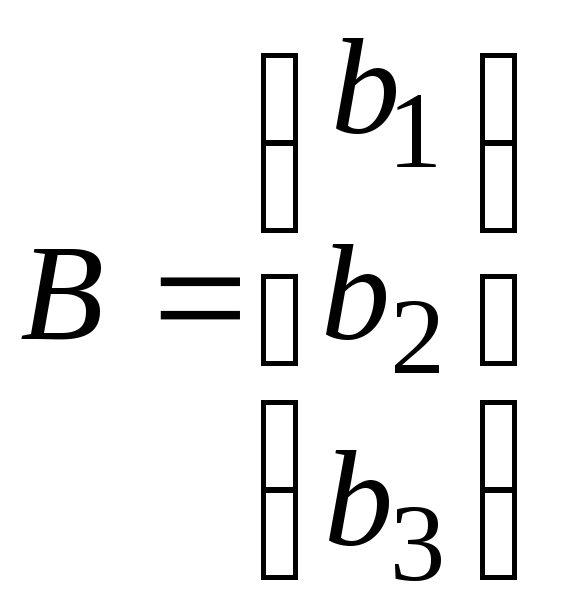, и решить графическим методом задачу линейного программирования

.

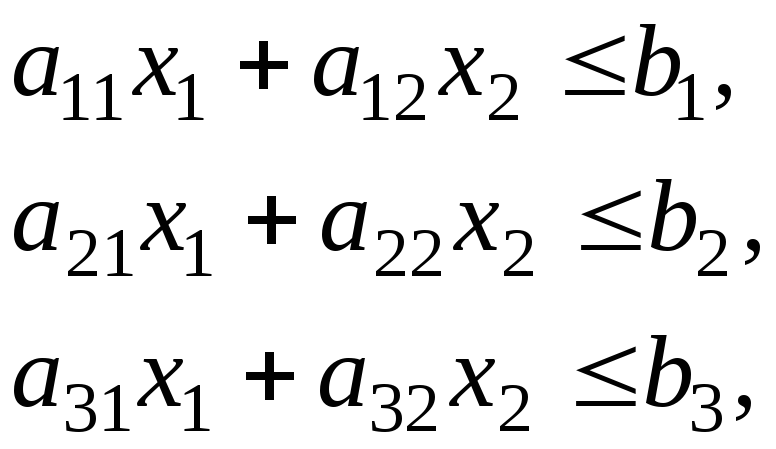
1.1. A= B=		1.2. A= B=
1.3. A=B=		1.4. A= B=
1.5. A= B=		1.6. A= B=
1.7. A= B=		1.8. A=B=

1.9. A= B=		1.10. A= B=
1.11. A=B=		1.12. A= B=
1.13. A=B=		1.14. A= B=
1.15. A= B=		1.16. A= B=
1.17. A= B=		1.18. A= B=
1.19. A= B=		1.20. A= B=
1.21. A= B=		1.22. A= B=
1.23. A= B=		1.24. A= B=

1.25. A= B=		1.26. A=B=
1.27. A= B=		1.28. A= B=
1.29. A= B=		1.30. A= B=
1.31. A= B=		1.32. A= B=
1.33. A= B=		1.34. A= B=
1.35. A=B=		1.36. A= B=
1.37. A= B=		1.38. A= B=
1.39. A= B=		1.40. A= B=

1.41. A=B=		1.42. A= B=
1.43. A=B=		1.44. A= B=
1.45. A= B=		1.46. A= B=
1.47. A= B=		1.48. A= B=
1.49. A=B=		1.50. A= B=
1.51. A= B=		1.52. A= B=
1.53. A= B=		1.54. A= B=
1.55. A= B=		1.56. A= B=

1.57. A= B=		1.58. A= B=
1.59. A=B=		1.60. A=B=
1.61. A= B=		1.62. A= B=
1.63. A= B=		1.64. A= B=
1.65. A= B=		1.66. A= B=
1.67. A= B=		1.68. A= B=
1.69. A= B=		1.70. A= B=
1.71. A= B=		1.72. A= B=

1.73. A=B=		1.74. A= B=
1.75. A= B=		1.76. A=B=
1.77. A= B=		1.78. A=B=
1.79. A=B=		1.80. A=B=
1.81. A=B=		1.82. A= B=
1.83. A=B=		1.84. A= B=
1.85. A= B=		1.86. A= B=
1.87. A= B=		1.88. A= B=

1.89. A= B=		1.90. A= B=
1.91. A= B=		1.92. A= B=
1.93. A= B=		1.94. A=B=
1.95. A= B=		1.96. A= B=
1.97. A= B=		1.98. A=B=
1.99. A=B=		1.100. A= B=
1.101. A= B=		1.102. A= B=
1.103. A= B=		1.104. A= B=

10