Karmazin_-_Teoria_Igr_Uchebnik / P13_3

Тема 13. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ МАТРИЧНЫХ ИГР

Для решения матричных игр с платежной матрицей размером или можно успешно использовать графический метод.

Пусть задана игра с платежной матрицей

У 1-го игрока  две чистые стратегии, у 2-го  три чистые стратегии. Смешанная стратегия 1-го игрока представляет собой совокупность двух чисел и , где обозначает вероятность выбора 1-й стратегии, а  вероятность выбора 2-й стратегии. В сумме и равны единице: . Смешанная стратегия 2-го игрока задается тремя числами, вероятностями выбора трех чистых стратегий: и , также дающих в сумме единицу: .

Геометрически смешанную стратегию 1-го игрока можно представить точкой на единичном отрезке:

Если 2-й игрок выбрал -ю стратегию, то математическое ожидание выигрыша 1-го игрока составит . Отложим на оси абсцисс единичный отрезок для представления смешанных стратегий 1-го игрока, на оси ординат будем откладывать ожидаемый выигрыш. Так как ожидаемые выигрыши  функции, линейные от и , то геометрическое место точек смешанных стратегий и ожидаемых выигрышей представляет собой прямую. Выигрыш 1-го игрока при , что соответствует 2-й чистой стратегии 1-го игрока при условии, что 2-й игрок выбрал -ю стратегию, составит . Если 1-й игрок выберет 1-ю чистую стратегию, , то его выигрыш составит . На перпендикуляре к оси абсцисс в точке откладываем выигрыши 1-го игрока, соответствующие его 2-й чистой стратегии: . А на перпендикуляре к оси абсцисс в точке откладываем выигрыши, соответствующие 1-й чистой стратегии: .

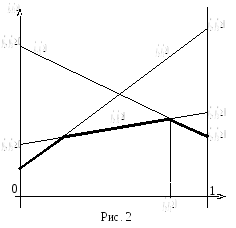
Соединяя прямой линией точки на левом перпендикуляре с точками на правом перпендикуляре, получим графики ожидаемых выигрышей 1-го игрока для каждой из чистых стратегий 2-го игрока.

Для каждой смешанной стратегии определяем наименьший (гарантированный) ожидаемый выигрыш

График функции является нижней границей множества прямых и на рис.2 выделен жирной линией. Та точка отрезка, в которой нижняя граница достигает наибольшего значения, соответствует искомой смешанной стратегии , высота максимума дает значение цены игры

.

По графику определяем номера прямых , точка пересечений которых имеет абсциссу , допустим, это и , и вычисляем точные значения вероятностей и из системы уравнений

Оптимальную смешанную стратегию 2-го игрока можно рассматривать как опорное решение задачи линейного программирования. Для игры с матрицей из структуры соответствующей задачи линейного программирования следует, что смешанная стратегия 2-го игрока имеет не более чем две ненулевые компоненты и не менее чем нулевых. Из соотношений двойственности задач обоих игроков номера ненулевых элементов определяются номерами прямых, пересечение которых определило оптимальную стратегию 1-го игрока. Согласно рисунку это прямые и , следовательно, , а компоненты определяем из уравнений

Пример 1. Найти решение игры с платежной матрицей

Прежде всего проверяем наличие седловой точки. Вычисляем: откуда нижнее значение игры  . Вычисляем: для верхнего значения откуда . Так как , то седловой точки нет, и задача не имеет оптимального решения в чистых стратегиях.

Решаем задачу в смешанных стратегиях, для этого строим графики математических ожиданий выигрыша первым игроком:

Нижнюю границу ожидаемых выигрышей первого игрока выделим жирной линией на рис. 13.3. Из графика видно, что гарантированный максимальный выигрыш находится в точке пересечения прямых и . Находим координаты точки пересечения из системы уравнений:

при этом цена игры составит . Оптимальную смешанную стратегию 2-го игрока находим из уравнений: , полагаем, что . Решая, получим .

Игра с платежной матрицей решается аналогично, только за основу берутся смешанные стратегии 2-го игрока. По ним строится ломанная, которая характеризует верхнюю границу ожидаемого выигрыша и на которой ищем точку с минимальной ординатой. Перейдем сразу к примеру.

Пример 2. Найти решение игры с платежной матрицей

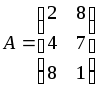
Проверяем наличие седловой точки. Вычисляем нижнее значение игры  и верхнее значение игры

. Так как , то седловой точки нет.

Решаем задачу в смешанных стратегиях. Смешанная стратегия 1-го игрока задается вектором вероятностей , где . Смешанная стратегия второго игрока  вектором вероятностей , где . Математическое ожидание проигрыша 2-го игрока для каждой чистой стратегии 1-го игрока задаются формулами:

.

Построим график, на оси абсцисс которого будем откладывать компоненты смешанной стратегии , а на вертикальных осях  величину ожидаемого проигрыша 2-го игрока.

Выделим верхнюю границу ожидаемого выигрыша (она же нижняя граница проигрыша 2-го игрока) жирной линией. Точка с минимальной ординатой на этой линии находится на пересечении прямых . Найдем координаты этой точки из системы уравнений

.

Получим и цену игры . Определим оптимальную стратегию 1-го игрока, так как 1-я стратегия неактивна, то полагаем , а остальные компоненты вычислим из уравнений:. Получим.

Задание 1. Для игры заданной платежной матрицей в упражнениях 13.1  13.102 найти нижнее и верхнее значения игры; оптимальные смешанные стратегии обоих игроков; цену игры.

Задание 2. Для игры заданной платежной матрицы , где из 13.1  13.102 найти нижнее и верхнее значения игры; оптимальные смешанные стратегии обоих игроков; цену игры.

12.1 A=		13.2 A=		13.3 A=
13.4 A=		13.5 A=		13.6 A=
13.7 A=		13.8 A=		13.9 A=
13.10 A=		13.11 A=		13.12 A=
13.13 A=		13.14 A=		13.15 A=
13.16 A=		13.17 A=		13.18 A=

13.19 A=		13.20 A=		13.21 A=
13.22 A=		13.23 A=		13.24 A=
13.25 A=		13.26 A=		13.27 A=
13.28 A=		13.29 A=		13.30 A=
13.31 A=		13.32 A=		13.33 A=
13.34 A=		13.35 A=		13.36 A=
13.37 A=		13.38 A=		13.39 A=
13.40 A=		13.41 A=		13.42 A=
13.43 A=		13.44 A=		13.45 A=
13.46 A=		13.47 A=		13.48 A=
13.49 A=		13.50 A=		13.51 A=
13.52 A=		13.53 A=		13.54 A=
13.55 A=		13.56 A=		13.57 A=

13.58 A=		13.59 A=		13.60 A=
13.61 A=		13.62 A=		13.63 A=
13.64 A=		13.65 A=		13.66 A=
13.67 A=		13.68 A=		13.69 A=
13.70 A=		13.71 A=		13.72 A=
13.73 A=		13.74 A=		13.75 A=
13.76 A=		13.77 A=		13.78 A=
13.79 A=		13.80 A=		13.81 A=
13.82 A=		13.83 A=		13.84 A=
13.85 A=		13.86 A=		13.87 A=
13.88 A=		13.89 A=		13.90 A=
13.91 A=		13.92 A=		13.93 A=
13.94 A=		13.95 A=		13.96 A=
13.97 A=		13.98 A=		13.99 A=
13.100 A=.		13.101 A=.		13.102 A=

169