10.2 Вероятность спонтанного излучения поляризованного электрона

Интерпретируя взаимодействие электрона с вторично квантованным полем излучения как возмущение, можно получить для вероятности излучения фотона в единицу времени в первом порядке теория возмущения формулу [192]:

,, (3.13)

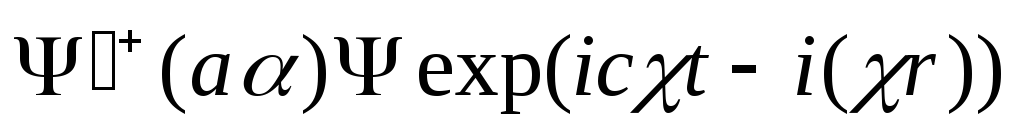
Здесь и- волновые функции начального и конечного состояний электрона определяемые как решения уравнения Дирака во внешнем электромагнитном поле, считающимся классическим. Далее,оператор, уничтожения фотона с импульсом,- четырехмерная матрица Дирака, связанная с двухрядными матрицами Паулисоотношением

(3.14)

Для изучения поляризационных свойств излучения амплитуду выберем в виде [192]

, , (3.15)

,

,,

- единичный вектор.

Используя сферическую систему координат для единичного вектора . Тогда

,,

,,

Здесь положим . Отметим, что подобный выбор векторов поляризацииисоответствует разложению излучения наикомпоненты линейной поляризации.

Для того, чтобы исследовать процессы с участием поляризованных электронов необходимо в явном виде выделить зависимость вероятности процессов от ориентации спина электрона в начальном и конечном состояниях.

Вероятность процесса с участием поляризованных электронов пропорциональна квадрату модуля матричного элемента, который всегда можно представить в виде

(3.16)

где ивекторы, определяющие ориентацию спина электрона в начальном и конечном состояниях,некоторое число,- вектор. С учетом (3.16) квадрат модуля матричного элемента приводим к виду

(3.17)

в этом выражении явно учитывается ориентация спина электрона, аналогичное выражение приводится в [12].

Если необходимо учитывать ориентацию спина электрона только в конечном состоянии, то усредняя в (3.17) по начальным спиновым состояниям, получим

(3.18)

Если просуммировать по конечным спиновым состояниям

(3.19)

В (3.17) векторы ипроизвольны, но если эти векторы совпадают, то (3.17) примет более простой вид

(3.20)

Нас в дальнейшем будет интересовать характер поведения электронного спина при спонтанном излучении в поле плоской волны. Это поведение полностью определяется вероятностью переходов с переворотом спина , где- спиновое число начального состояния,- спиновое число конечного состояния. Это можно объяснить тем, что поскольку вероятность зависит от начального (конечного) спинового состояния в явном виде, тогда различные спиновые состояния имеют разную устойчивость и при излучении спин электрона приобретает преимущественную ориентацию. Оказывается, что для волны круговой поляризации, т.е. для фотонов, имеющих определенную спиральность и спин которых ориентирован в одном направлении, наблюдается очень сильная зависимость вероятности переходов с переворотом спина от начального спинового числа[182, 183, 192, 193]. Физически очевидно, что можно обобщить и на случай электромагнитной волны произвольной интенсивности, что является физически объяснимым.

В связи с этим примем к рассмотрению монохроматическую плоскую волну круговой поляризации, потенциал которой будем определять формулой

,(3.21)

Здесь - амплитуда напряженности электрического поля волны,- частота волны,g=1 иg=-1 соответствуют право и лево поляризованной волнам.

Параметр , заданный 3.5 примет вид

(3.22)

Расчет матричных элементов процесса излучения для выбранного нами типа волны выполняется в аналитическом виде до конца [184-189,109].

Пусть вектор импульса излученного фотона есть . Вектор имеет вид

,,

,,(3.23)

где ,- сферические углы, определяющие направлениераспространения излученного фотона,- частота излучения.

Определим при помощи законов сохранения:

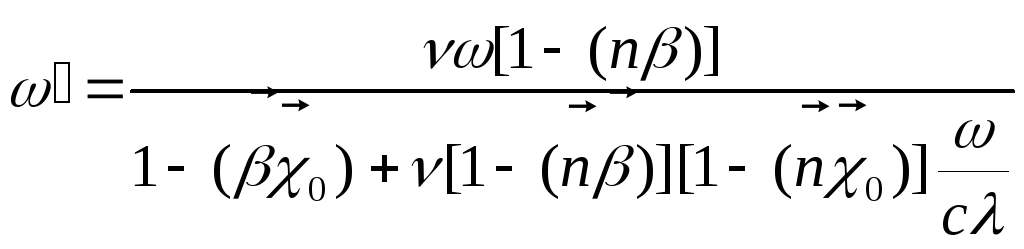(3.24)

где - номер излучаемой гармоники. Отметим, что (3.24) пригодна для любой поляризации плоской монохроматической волны.

В предшествующих работах при расчетах полагали в начальном состоянии , либо,(это соответствует полному отсутствию дрейфа () в начальном состоянии). Тем не менее удалось выяснить, что это не упрощает расчетов, поскольку переход в систему координат, где, соответствует прео6разованию угловых переменных,. В дальнейшем вместо углов,будем использовать новые углы,связанные соотношениями с,:

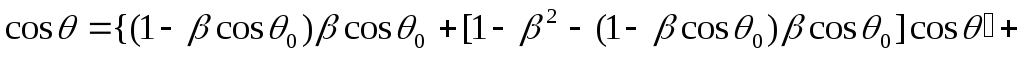
(3.25)

,

,

,

,

,,

Частоту фотона из (3.24) определим через углы,следующим образом

,(3.26)

Эти замены позволяют значительно упростить вычисления вероятности Wизлучения с учетом ориентации начального (спиновый вектор, спиновое число) и конечного (спиновый вектор, спиновое число) спинов, её можно представить как

, (3.27)

,

,

,

,

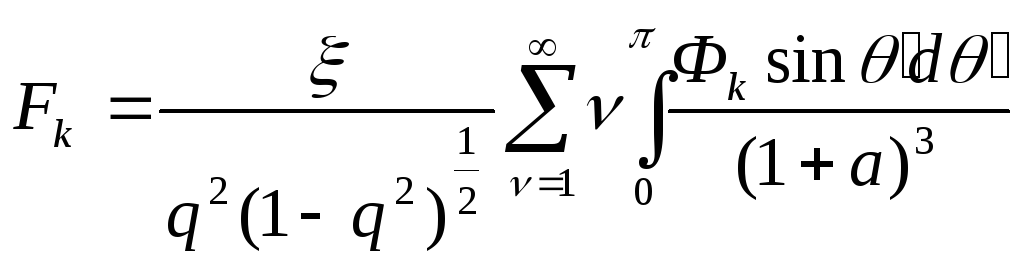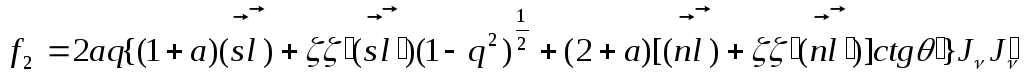
где ,- функция Бесселя и ее производная,

,(3.28)

Для вектора справедливо соотношение

,(3.29)

Таким образом, единичный вектор параллелен конечному поперечному импульсуэлектрона в той системе координат, в которой в начальном состоянии поперечный импульс.