
шпоры по Физике 2семестр
.docx|
М П.Вектор магн индукции. Принцип суперпоз для М П.Сила Ампера. М
п-силовое поле,возник вокруг проводников
с током и пост магнитов. М п действует
только на
движущиеся
в этом поле эл заряды. Определить поле
можно с помощью пробников (рамка с
током, маг. стрелка) Направл положит
нормали определ пр-лом правого винта. Вектор магн индукции явл количественной хар-кой м п.
З-н
Ампера |
Сила Лоренца. Джиж заряженных частиц в эл и магн полях. Сила действующ на эл.заряд Q движущ в м п со скоростью v назыв силой Лоренца. F=Q[vB]. Направл силы Лоренца определ по правилу левой руки. М п не действует на покоящийся заряд. Если на движущ заряд помимо м п действует эл.поле то результирующ сила=векторной сумме силF=QE+Q[vB]. Если
частица влетает под углом a
в магн поле то траектория движения-спираль
F
=q
E+q[VB]
F=Fэл+Fм
q(φ1-φ2)=mV2/2 q/m=V2/2∆φ |
Поток
и циркуляция магнитного поля.
В однор
м п, модуль вектора индукции которого
равен В,
помещен плоский замкнутый контур
площадью S.
Нормаль n
к плоскости контура составляет угол
a
с направл вектора магн индукции В.
Магн потоком
через поверхность называется величина
Ф, определяемая соотношением:
Φ=B·S·сos α
Ед
изм-1Вебер(Вб).1Вб=1Тл·1 м2
Магн поток
через контур максимален,если пл-ть
контура перпендик м п. Значит угол α
равен 00
. Тогда магн поток рассчитывается по
формуле: Φmax
= B · S Магн
поток через контур=0,если контур
распологается || м п.
Значит
угол α равен 900
. Циркуляция
вектора В по произвольному замкнутому
контуру равна произведению магнитной
постоянной на сумму токов охватываемых
этим контуром.
|
|||
|
М
П прямолин проводника с током. З-н
Био-Савара.
Рис:Связь между направл тока в прямолин проводнике и напр линий м п, создаваемого этим током; а) ток направлен сверху вниз; б) ток направлен снизу вверх, эл заряды есть и не сущ магнитных. Поэтому линии эл поля идут от заряда к заряду, а у м п нет ни начала ни конца, и линии его имеют замкнутый хар-ер. Взаимную связь между направл тока и направл поля, им создаваемого, легко запомнить при помощи правила буравчика. Если ввинчивать буравчик так, чтобы он шел по направл тока, то направл вращения его ручки укажет направление поля. М П прямого тока:
где dl — вектор, по модулю равный длине dl элем проводника и совпадающий по направл с током, r — радиус-вектор, проведенный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направл dB перпендик dl и r, т. е. перпендик пл-ти, в которой они лежат,и совпадает с касател к линии магн индукции. Это направл мб найдено по пр-лу нахожд линий магн индукции: направл вращения головки винта дает направл dB, если поступат движ винта соответствует направл тока в элементе.
На
рис изображена такая картина линий,
полученная с помощью железных опилок
для поля длинного прямолин проводника
и для поля кругового витка с током.
Линии м п имеют вид замкнутых линий
М П кругового проводника с током: Пусть соленоид длиной l, во много раз превышающей его диаметр, имеет N витков, по которым течет ток силой I. Если соленоид находится в вакууме (или воздухе), то магн индукция поля в нем численно равна B0 = μ0 IN / l = μ0 In, где n = N/l; In – число ампер-витков, приходящихся на единицу длины соленоида; μ0 – магнитн постоянная, характеризующая м п в вакууме. |
Виток с током в м п. Момент сил, действующ на виток с током в м п. Основн ур-я магнитостатики в вакууме.
М
п
витка с током,
или контура тока, показано рисунке.
Направл линий магн индукции вдоль
оси витка укажет магн стрелка,
помещенная в его центре. Две
противоположные стороны обтекаемой
током
поверхности можно сопоставить с двумя
полюсами магн стрелки: сторону, из
которой линии магн индукции выходят
– с северным полюсом магн стрелки, а
в которую они входят – с южным.
Момент
сил,
действующих на виток с током:
в вакууме
Циркуляция вектора В по произвольному замкнутому контуру = произведению магн постоянной на сумму токов охватываемых этим контуром. n- число проводников с током которые охватываются этим проводником. Положительным считается ток направление которого образует направлением обхода контура правовинтовую сист. 2) Теорема Гаусса-Остроградского: Поток вектора магн. инд сквозь любую замкнутую поверхность = 0 : В сквозь соленоид. Магнитная инд
однородного
поля внутри соленоида с сердечником с магнитной проницаемостью μ = B=μ0μNI/l , сквозь 1-ин виток магн. поток Ф1=BS а полный наз. потокосцеплением Ψ=Ф1N=NBS=μ0μ(N2I/l)S.
|
|
|||
|
Энергия
м п. Плотность энергии пост м п в
вещ-ве. Кривая намагничивания.
Гистерезис.
Энергия м п, которое связано с контуром
|
Магн
поток. Электромагн индукц Пр-ло Ленца.
Явл самоиндукции и взаимной индукции.
Электромагн
индукц: в
замкнутом проводящем контуре при
изменении потока магн индукции,
охватываемого этим контуром возник
эл ток, назыв индукционным. З-н Фарадея:
ЭДС электромагн индукц в замкнутом
контуре численно = и противоположна
по знаку скорости измен магн
потока,сквозь поверхность, огранич
этим контуром. εi
= - dФ/dt,
где
Ф-магн поток, t-время.
Возникнов
ЭДС индукции в проводящем контуре
при изменен в нём силы тока называют
самоиндукцией.
Пр-ло
Ленца
Индукц ток в контуре имеет всегда
такое направл , что создаваемое им м
п препятствует изменению магн потока,
вызвавшего этот индукц ток. Явл
самоиндукции и взаимной индукции:
возникнов ЭДС индукции в проводящем
контуре при измен в нём силы тока над
самоиндукцией:
|
Индуктивность. ЭДС самоиндукции. Токи при замык и размык эл цепи. Индуктивность: если соленоид пустой: L=μ0n2V, V=Sl-объём катушки. Если соленоид не пустой: L=μ0μn2V. ЭДС самоиндукц: εс = - dФ/dt. Индуктивность: Ф=LI. Токи при замык и размык эл цепи: при всяком изменении силы тока в проводящем контуре возник ЭДС самоиндукции, в результате чего в контуре появл доп токи, называемые экстратоками самоиндукции. При отключ источника тока сила тока убывает по экспоненциальному закону: чем больше L цепи и меньше её сопротивл, тем больше τ и => тем медленнее уменьш ток в цепи при еёразмык. I=I0e-t/τ, где τ-пост.,называемая временем релаксации. |
|||
|
 =0-ур-е
затух колеб =0-ур-е
затух колеб
 -коэф
затухания, -коэф
затухания,
 -собственная
частота. Для β<< -собственная
частота. Для β<< q=qm*e-βtcos(ωt+α)
q=qm*e-βtcos(ωt+α)

 Д= Д= -логарифм
декремент. Добротность: Q=П/Д -логарифм
декремент. Добротность: Q=П/Д
|
Вынужд электрич колеб. Резонансные кривые для напряжения и силы тока. Вынужденные электрические колебания. Колебания, возникающие под действием внешней периодически изменяющейся ЭДС. Полное сопротивление цепи, состоящей из резистор с R, конденсатора с RC, и катушки индуктивности с RL
Резонансными
кривыми
называются зависимости тока и
напряжения от частоты. Важной хар-кой
резонансного контура является
добротность
Q, определяемая отношением напряжения
на индуктивном (емкостном) элементе
к входному напряжению:
или
можно записать:
|
Вихревое эл поле. Ток смещения. Сист уравн Максвелла в интегральной и дифференц формах.Эл поле, возникающее при измен м п, имеет совсем другую структуру, чем электростатическое. Оно не связано с эл зарядами, и его линии напряжённости не могут на них начинаться и кончаться, а представляют собой они замкнутые линии, подобные линиям индукции м п. Это так называемое вихревое эл поле. Для установления колич соотношений м-ду изменяющимся эл полем и вызываемым им м п Максвелл ввёл ток смещения. М-ду обкладками заряжающегося конденсатора имеется переменное эл. поле поэтому через кон-р протекают токи смещения, причем в тех участках где отсутствуют проводники.
плотность тока в смещениях. в
диэлектриках: ток смещения по своей сути – изменяющееся со временем эл. поле. Уравнения Максвелла для электромагнитного поля в интегральной и дифференциальной формах.
источниками эл. поля могут быть либо эл. заряды, либо изменяющиеся по времени м поля, а м поля могут возбуждатся либо движущимися эл. зарядами либо переменными эл. полями. дифференциальная форма
|
|||
|
Плотность потока энергии электромагн поля. Электромагн волны. Волновое ур-е. Скорость распространения электромагн волн.
|
Электромагн
природа света. Законы геометрич
оптики. Оптическая длина пути. На
основании своих теоретич исследований
Максвелл сделал вывод: свет имеет
электромагнитную природу. Электромагнитная
природа света
была подтверждена в опытах Герца,
показавшего, что электромагнитные
волны, подобно свету на границе раздела
двух сред, испытывают отражение и
преломление. Основные законы
геометрической оптики были известны
задолго до установления физической
природы света. З-н
прямолин распростр света:
в оптически однор среде свет распростр
прямолин.З-н
отраж света:падающий
и отраженный лучи, а также перпендикуляр
к границе раздела 2ух сред, восстановленный
в точке падения луча, лежат в одной
пл-ти (пл-ть
падения).
Угол отражения γ равен углу падения
α. З-н
преломления света:
падающий и преломленный лучи, а также
перпендикуляр к границе раздела двух
сред, восстановленный в точке падения
луча, лежат в одной плоскости. Отношение
синуса угла падения α к синусу угла
преломления β есть величина, постоянная
для двух данных сред:
dl
= nds.
Полная
оптическая длина пути находится
интегрированием:
|
Принцип суперпозиции волн. Интенсивность при сложении колебаний. Понятие о когерентности. Временная и пространственная когерентность. Интерференция. Принцип суперпозиции волн заключается в след: в лин средах волны распростр независимо друг от друга, т.е. волна не изменяет св-ва среды, и другая волна распространяется так, будто первой волны нет. Это позволяет вычислять итоговую волну как сумму всех волн, распространяющихся в данной среде. Понятие о когерентности:это согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Любой немонохромат свет можно представить в видесовокупности сменяющих друг друга независимых гармонических цугов. Ср продолжит одного цуга τког наз временем когерентности. Когер колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности воли, назыв временной когерентностью. 2 источника, размеры и взаимное расположение которых позволяют наблюдать интерференцию, назыв пространственно-когерентными.Интерферен:при налож когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возник max, а в других min интенсивности. (интерфер света) |
|||
|
Опыт
Юнга. Ширина интерференц полосы.
Способы наблюд интерфер. Опыт
Юнга: источником света служит ярко
освещённая щель S,
от которой световая волна падает на
2 узкие равноудалённые щели S1
и S2,||
щели S.
Таким образом, щели S1
и S2
играют роль когерентных источников.
Интерференционная картина наблюдается
на экране:
|
Интерфер
при отражении от тонких пластинок.
Полосы равного наклона и равной
толщины. Кольца Ньютона. Интерфер
при отраж от тонких пластинок:
|
Принцип
Гюйгенса-Френеля. Дифр Френеля. Дифр
Фраунгофера. Дифр на круглом отверстии
и на круглом полупрозрачном диске.
Принцип
Гюйгенса-Френеля: световая сила,
возбуждающая каким-либо источником
S
может быть представлена как результат
суперпозиции когерентных вторичных
волн, излуч фиктивными источниками.
Таким образом, волны, распространяющиеся
от источника, являются результатом
интерференции всех когерентных
вторичных волн. Дифракция на круглом
отверстии:
А=А1/2±Am/2 На диске:
|
|||
|
Дифракц рентгеновских лучей. Формула Вульфа-Брэгга. Понятие о голографии. Дифракция рентгеновских лучей - рассеяние рентгеновских лучей кристаллич объектами, при котором в опредх направл появляются дифрагированные пучки - результат интерференции вторичного рентгеновского излучения, возникающего при взаимодействии первичного излучения с электронными оболочками атомов. Формула Вульфа-Брэгга:2dsinθ=mλ, d~10-10м λ~5*10-7-не наблюд дифракции. λ~10-8-10-12м-наблюд дифракция. Гомография-особый способ записи и последующего восстановления волнового поля, основанный на регистрации интерференционной картины. Она обязана своим возникновением законам волновой оптики-законам интерференции и дифракции. |
Дисперсия.
Нормальная и аномальная дисперсии.
Групповая и фазовые скорости. Дисперсией
называется зависимость показателя
преломления n
вещества от частоты J
света или зависимость фазовой скорости
V
световых волн от его частоты J Д=dn/dλ [Д]=м-1 Дисперсия
нормальная:
Аномальная:
|
Естественный
и поляризованный свет. Степень
поляризации. Поляризаторы и анализаторы.
Закон Малюса. Свет
со всевозможными равновероятными
ориентациями вектора Е (и, следовательно,
Н) называется естественным.Свет, в
котором направления колебаний
светового вектора каким-то образом
упорядочены, называется поляризованным.
Так, если в результате каких-либо
внешних воздействий появляется
преимущественное (но не исключительное!)
направление коле¬баний вектора Е, то
имеем дело с частично поляризованным
светом. Свет, в котором вектор Е (и,
следовательно, Н) колеблется только
в одном направлении, перпендикулярном
лучу, называется плоскополяризованным
(линейно поляризованным).Степенью
поляризации называется величина р= |
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
||||



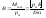 Магн
индукция однородн м п определ max
вращающим моментом действующ на рамку
с магн.моментом=1, когда нормаль
перпендик направл поля. Принцип
суперпоз м п:
если м п создано несколькими проводниками
с токами, то вектор магн индукции в
какой-либо точке этого поля равен
векторной сумме магн индукций,
созданных в этой точке каждым током
в отдельности:
Магн
индукция однородн м п определ max
вращающим моментом действующ на рамку
с магн.моментом=1, когда нормаль
перпендик направл поля. Принцип
суперпоз м п:
если м п создано несколькими проводниками
с токами, то вектор магн индукции в
какой-либо точке этого поля равен
векторной сумме магн индукций,
созданных в этой точке каждым током
в отдельности: Сила
Ампера = произвед вектора магн индукции
на силу тока, длину участка проводника
и на sin
угла м-ду магн индукцией и участком
проводника.
Сила
Ампера = произвед вектора магн индукции
на силу тока, длину участка проводника
и на sin
угла м-ду магн индукцией и участком
проводника.
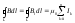

 З-н
Био-Савара-Лапласа для
проводника с током I, элемент dl которого
создает в некоторой точке А индукцию
поля dB, записывается в виде
З-н
Био-Савара-Лапласа для
проводника с током I, элемент dl которого
создает в некоторой точке А индукцию
поля dB, записывается в виде



 Осн ур-я магнитостатики в вакууме: 1)
Закон
полного тока для магн поля
Осн ур-я магнитостатики в вакууме: 1)
Закон
полного тока для магн поля
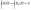
 =
= +I
+I ),
если L=соnst,
то
),
если L=соnst,
то
 Явл возникнов ЭДС в одном из контуров
при измен силы тока в другом называют
взаимной индукцией, а коэф пропорц L
21
и L12
наз
взаимной индуктивностью контуров L
21=L12
Явл возникнов ЭДС в одном из контуров
при измен силы тока в другом называют
взаимной индукцией, а коэф пропорц L
21
и L12
наз
взаимной индуктивностью контуров L
21=L12





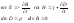
 Ширина
интерференц полосы: назыв расстояние
м-ду 2мя соседними max
(min).
Ширина
интерференц полосы: назыв расстояние
м-ду 2мя соседними max
(min).
 .
Способы наблюд интерфер: зеркало
Френеля, Бипризма Френеля
.
Способы наблюд интерфер: зеркало
Френеля, Бипризма Френеля max:
max: min:
min: Полосы
равного наклона:
интерференционыые полосы возникающие
в результате наложения лучей, падающих
на плоскопараллельную пластинку под
одинаковыми углами.
Полосы равной толщины:
интерференц полосы, возникающие в
результате интерференции от мест
одинаковой толщины. Кольца
Ньютона:
Полосы
равного наклона:
интерференционыые полосы возникающие
в результате наложения лучей, падающих
на плоскопараллельную пластинку под
одинаковыми углами.
Полосы равной толщины:
интерференц полосы, возникающие в
результате интерференции от мест
одинаковой толщины. Кольца
Ньютона:
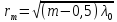 R
–для светлых колец.
R
–для светлых колец.
 -для
тёмных колец
-для
тёмных колец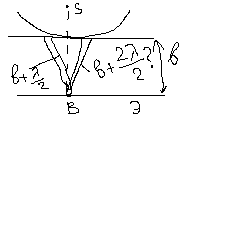
 А=Аm+1/2
Дифра́кция
Френе́ля
— дифракционная
картина,
которая наблюдается на небольшом
расстоянии
от препятствия, по условиям, когда
основной вклад в интерференционную
картину
дают границы экрана.
Дифракционная картина для дифракции
Френеля
зависит от расстояния между экранами
и от расположения источников света.
В точке наблюдения волны или усиливают
друг друга, или гасятся в зависимости
от разности
хода.
А=Аm+1/2
Дифра́кция
Френе́ля
— дифракционная
картина,
которая наблюдается на небольшом
расстоянии
от препятствия, по условиям, когда
основной вклад в интерференционную
картину
дают границы экрана.
Дифракционная картина для дифракции
Френеля
зависит от расстояния между экранами
и от расположения источников света.
В точке наблюдения волны или усиливают
друг друга, или гасятся в зависимости
от разности
хода.
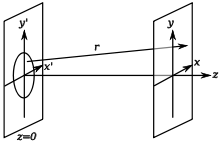 Дифракция Фраунгофера —
случай дифракции,
при котором дифракционная картина
наблюдается на значительном расстоянии
от отверстия или преграды. Расстояние
должно быть таким, чтобы можно было
пренебречь в выражении для разности
фаз членами порядка
Дифракция Фраунгофера —
случай дифракции,
при котором дифракционная картина
наблюдается на значительном расстоянии
от отверстия или преграды. Расстояние
должно быть таким, чтобы можно было
пренебречь в выражении для разности
фаз членами порядка
 ,
что сильно упрощает теоретическое
рассмотрение явления. Здесь z
— расстояние от отверстия или преграды
до плоскости наблюдения, λ
— длина волны излучения, а ρ
— радиальная координата рассматриваемой
точки в плоскости наблюдения в полярной
системе координат. Иными словами,
дифракция Фраунгофера наблюдается
тогда, когда число зон
Френеля
F<<1,
при этом приходящие в точку волны
являются практически плоскими.
,
что сильно упрощает теоретическое
рассмотрение явления. Здесь z
— расстояние от отверстия или преграды
до плоскости наблюдения, λ
— длина волны излучения, а ρ
— радиальная координата рассматриваемой
точки в плоскости наблюдения в полярной
системе координат. Иными словами,
дифракция Фраунгофера наблюдается
тогда, когда число зон
Френеля
F<<1,
при этом приходящие в точку волны
являются практически плоскими.

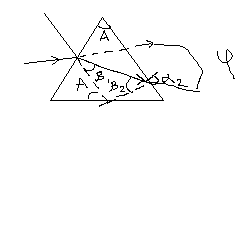 φ≈А(n-1)
φ≈А(n-1)
