


Явно Y=f(x) Не явно F(x,y)=0 В геометрической
форме Уравнением
линии на плоскости, в прямоугольной
системе координат называется уравнение
вида
Определение
Множество точек
находящихся одновременно на двух
поверхностях
Способы
задания
Определение
Пересечение двух
поверхностей В параметрической
форме Порядок линии

![]() x=x(t)
x=x(t)![]() y=y(t)
y=y(t)![]()

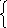


![]()
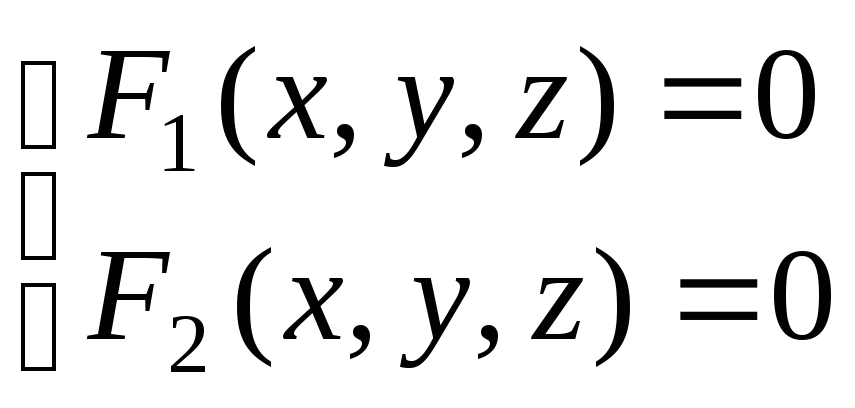
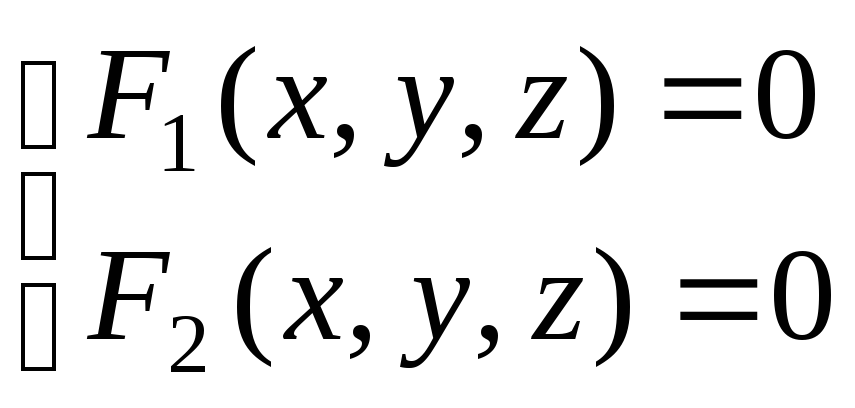
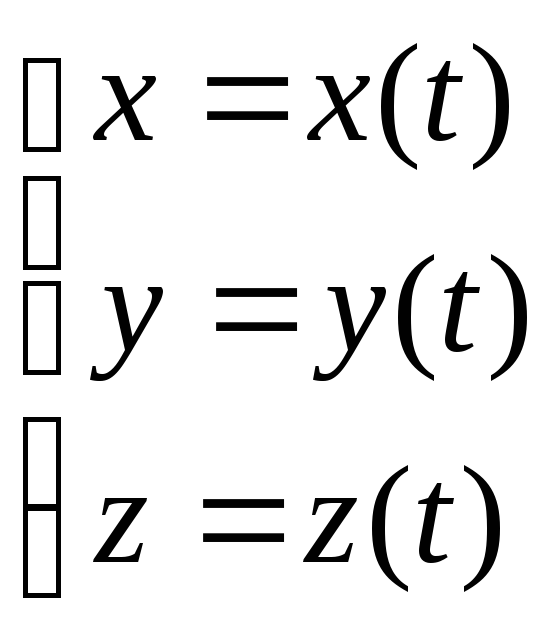












Способы задания
В различных системах координатах

В декартовой В полярной


y
x
![]()
![]()
![]()
![]() - явно
- явно![]() - неявно
- неявно

В параметрической
форме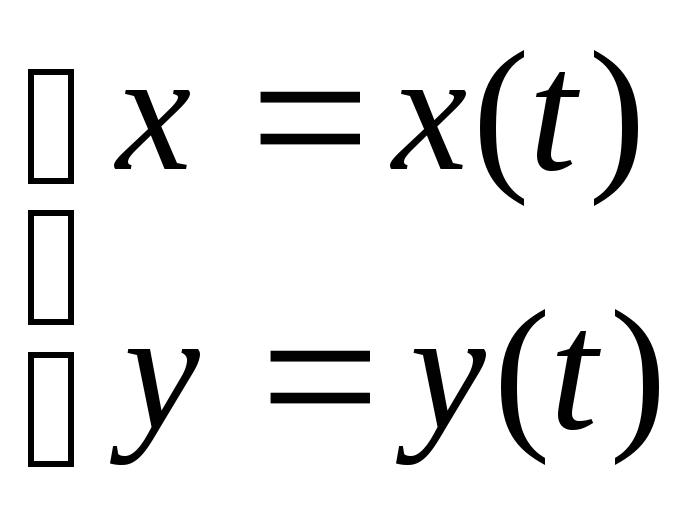
Частный случай Линия первого порядка
– прямая в пространстве задана как
пересечение плоскостей:
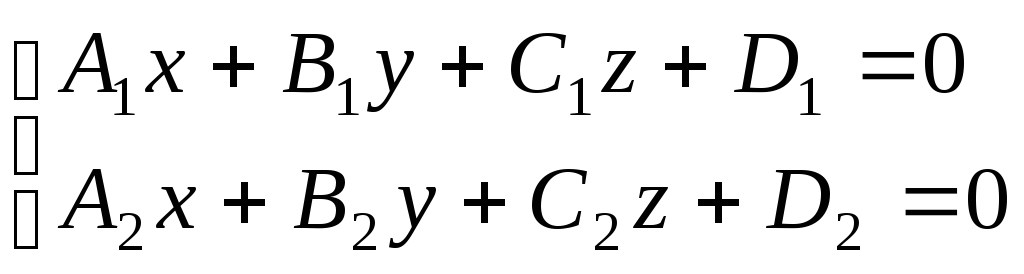
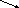
 -ур-ние
окружности (1) в параметрической
форме
-ур-ние
окружности (1) в параметрической
форме
|
прямая в пространстве |
прямая на плоскости |
||
|
Векторно-параметрическое уравнение |
Векторное уравнение |
||
|
|
|
|
|
|
Параметрическое уравнение |
|||
|
|
|
||
|
Каноническое уравнение |
|||
|
Attention!!! Более корректно: канонические уравнения. Подумайте, почему? |
Attention!!!
|
||
|
Уравнение прямой по двум точкам |
|||
|
|
|
||
|
Общее уравнение |
|||
|
|
Координатная форма уравнения (1)
|
||
|
Переход от общего к каноническому |
У |
||
|
|
|
||
|
Уравнение в «отрезках»
|
|||
Геометрические задачи на положение и взаиморасположение прямых
на плоскости
Угол между прямыми
|
|
|
|
|
|
|
|
|
|
|
|
Условия параллельности
|
|
|
|
|
|
|
|
|
|
|
|
Условия перпендикулярности
|
|
|
|
|
|
|
|
|
|
|
|
Расстояние от точки до прямой на плоскости
|
|
|
|
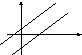
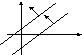
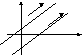
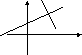
Влияние коэффициентов на положение прямой на плоскости
|
y
x
|
x x
|
|
x
|
x
|
|
x
|
x
|

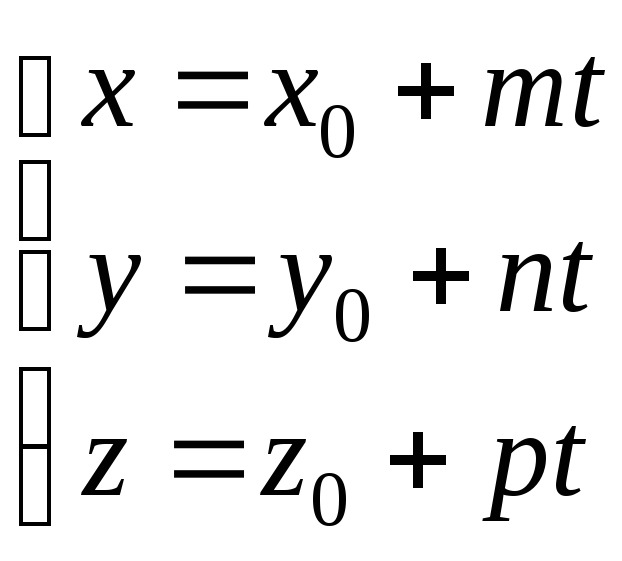

 равнение
с угловым коэффициентом
равнение
с угловым коэффициентом



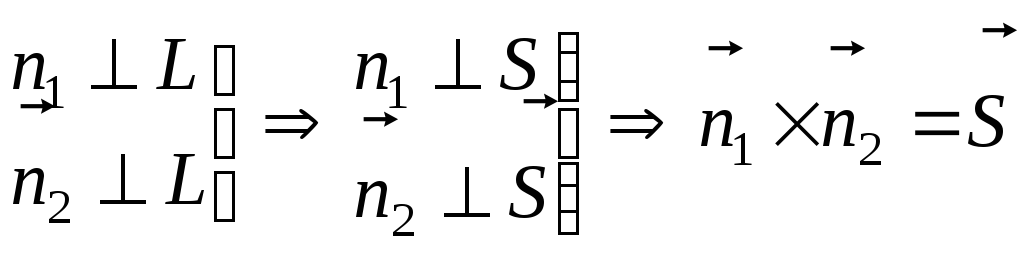





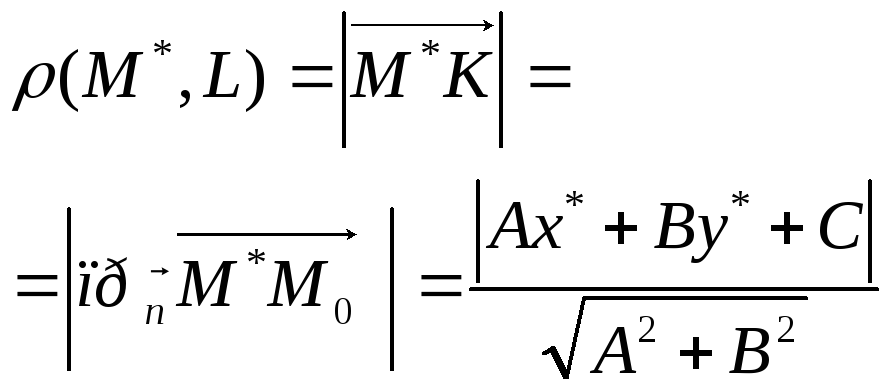
 y
y
y
y y
y y
y y
y y
y