
Гидро- и гемодинамика.
Гидродинамика – раздел физики, изучающий основные законы движения жидкостей и их взаимодействие с окружающими твёрдыми телами.
Гемодинамика– раздел физики, изучающий движение крови по сосудистой системе. Основа гемодинамики – гидродинамика.
Важнейшие свойства жидкости – поверхностное натяжение и вязкость.
Поверхностное натяжение.
На молекулу жидкости, расположенную у её поверхности действуют силы взаимодействия с соседними молекулами жидкости и газа. Причём векторная сумма всех сил, действующих со стороны жидкости, больше, чем со стороны газа. В результате молекула с поверхности жидкости переходит в глубину. Чтобы переместить эту молекулу на поверхность, ей нужно сообщить дополнительную энергию, т.е. совершить работу. Отношение работы по перемещению молекул на поверхность к площади этой поверхности – постоянная величина для данной жидкости при данной температуре – коэффициент поверхностного натяжения.
![]()
Коэффициент поверхностного натяжения– величина, численно равная работе по созданию единицы площади свободной поверхности жидкости при постоянной температуре. Размерность: Дж/м2.
Коэффициент поверхностного натяжениязависит от строения жидкости (коэффициент поверхностного натяжения растворов меньше, чем растворителя) и температуры (с увеличением температуры он уменьшается).
Коэффициент поверхностного натяжения– отношение силы поверхностного натяжения к длине контура (силы поверхностного натяжения направлены перпендикулярно контуру). Размерность: Н/м.
![]()
Смачивание– явление, возникающее, когда силы поверхностного натяжения на границе твёрдого тела с газом больше, чем на границе твёрдого тела с жидкостью, при котором молекула поверхностного слоя жидкости движется вверх по стенке, увлекая за собой соседние молекулы. Угол между твёрдой поверхностью и касательной к поверхности жидкости называют краевым. В данном случае он менее 900. Капля растекается по поверхности жидкости.
Несмачивание – явление, возникающее, когда силы поверхностного натяжения на границе твёрдого тела с газом меньше, чем на поверхности твёрдого тела с жидкостью, при котором молекула поверхностного слоя жидкости движется вниз по стенке, увлекая за собой соседние молекулы. Краевой угол более 900. Жидкость на поверхности собирается в капли.
Под искривлённой поверхностью жидкости создаётся дополнительное давление – давление Лапласа.
![]() ,
гдеR- радиус трубки,r– радиус мениска, Ф – краевой угол.
,
гдеR- радиус трубки,r– радиус мениска, Ф – краевой угол.
Капиллярность – движение жидкости в капилляре под действием давления Лапласа.
Методы измерения коэффициента поверхностного натяжения:
1. Метод Ребиндера (максимального давления в пузырьке воздуха).
С открытием крана аспиратора давление в системе падает ниже атмосферного:
![]() .
.
Уровни жидкости в манометре меняются:
![]() .
.

![]()
![]()
![]()
2. Метод отрыва капли.

Вязкость.
Вязкостью,или внутренним трением жидкостей и газов, называется их свойство оказывать сопротивление перемещению одной своей части относительно другой. Вязкость обусловлена наличием межмолекулярных сил притяжения (поэтому понятно то, что вязкость жидкостей больше вязкости газов).
Реальная жидкостьобладает вязкостью. Жидкость, не обладающая вязкостью и к тому же абсолютно несжимаемая, называетсяидеальной. Идеальная жидкость – физическая абстракция, но маловязкие жидкости по ряду свойств приближаются к идеальной.
Вязкость проявляется во взаимном влиянии различно двигающихся слоёв жидкости (газа): быстрее движущийся слой ускоряет движение близлежащих слоёв, медленно движущийся – тормозит.
Обусловленные вязкостью силы действуют по касательной к слоям, а величина их определяется уравнением Ньютона:
![]() ,
где
,
где
F– сила внутреннего трения
![]() -эта–коэффициент
пропорциональности, коэффициент
вязкости, динамическая вязкость
-эта–коэффициент
пропорциональности, коэффициент
вязкости, динамическая вязкость
S– площадь соприкасающихся слоёв
![]() - градиент скорости – быстрота изменения
скорости по мере изменения расстояния
между слоями (по перпендикуляру).
- градиент скорости – быстрота изменения
скорости по мере изменения расстояния
между слоями (по перпендикуляру).
Формулировка: сила внутреннего трения пропорциональна площади соприкасающихся слоёв и градиенту скорости.
Е сли
выделить в жидкости 2 слоя со скоростями
сли
выделить в жидкости 2 слоя со скоростями![]() и
и![]() на
расстоянии
на
расстоянии![]() ,
то
,
то![]() .
.
 Измеряется в [Паскаль.секунда]
Измеряется в [Паскаль.секунда]
![]() численно равна силе внутреннего трения
между слоями жидкости единицы площади
при единичном градиенте скорости.
численно равна силе внутреннего трения
между слоями жидкости единицы площади
при единичном градиенте скорости.
Динамическая вязкостьзависит от рода жидкости (газа) и от температуры. С ростом температуры скорость теплового движения и кинетическая энергия молекул увеличивается. Однако, влияние этого эффекта на внутреннее трение в жидкостях и газах противоположно. В жидкостях легче преодолеваются силы межмолекулярного притяжения, и вязкость уменьшается. В газах молекулы, исходно расположенные на весьма больших расстояниях, часто оказываются рядом и сталкиваются, в результате чего вязкость увеличивается.
Наряду с понятием динамической вязкости существует понятие вязкости кинематической,более полно учитывающей влияние внутреннего трения на характер течения жидкости или газа.
![]()
Кинематическая вязкостьравна
отношению динамической вязкости к
плотности жидкости и измеряется в![]() .
.
Методы измерения вязкости:
Метод стокса (падающего шарика) – основан на измерении движения твёрдого тела в вязкой жидкости.
Установка: колба с жидкостью, шарик
Сила трения, возникающая при движении
твёрдого тела в вязкой жидкости – сила
Стокса:
![]() ;
сила тяжести:
;
сила тяжести:![]() ;
сила Архимеда:
;
сила Архимеда:![]() .
.
Расчётная формула:

Метод капиллярной вискозиметрии – основан на формуле Пуазейля.
вискозиметр Оствальда
Расчётная формула:
![]()
вискозиметр Гесса
Расчётная формула:
![]()
Классификация жидкостей по их реологическим показателям:
Реология– раздел механики, занимающийся изучением деформаций и течения материалов.
Различают жидкости ньютоновские и неньютоновские. Коэффициент вязкости ньютоновских жидкостей не зависит от градиента скорости, т.е. при неизменной температуре и для данной жидкости это величина постоянная. Именно для таких жидкостей имеет место пропорциональность между градиентом скорости и силой вязкости; говорят, что эти жидкости подчиняются уравнению Ньютона.
Коэффициент вязкости неньютоновских жидкостей зависит от градиента скорости, причём эта зависимость может быть двоякой: с ростом градиента скорости у вязко-упругих жидкостей коэффициент вязкости увеличивается, а у вязко-пластичных – уменьшается.
Следовательно, сила внутреннего трения вязкоупругих жидкостей растёт быстрее, чем это следует из уравнения Ньютона, а вязкопластичные – напротив, медленнее.

![]() в/уFв/у
в/уFв/у
ньют ньют
в/пл
в/пл
кровь
0 ![]() 0
0![]()
Ламинарное и турбулентное течение жидкостей. Критерий Рейнольдса.
Различают ламинарное и турбулентное течение жидкости.
При ламинарном течениив жидкости можно условно выделить не перемешивающиеся слои, скорость движения частиц жидкости в каждой точке потока при этом не меняется со временем, т.е. течение является также стационарным.
При турбулентном течениив каждой точке скорости частиц беспорядочно изменяются со временем, образуются случайные вихри и слои внутри жидкости выделить нельзя.
Характер течения жидкости по трубам зависит от параметров, как самой жидкости, так и трубы. Математически эта зависимость описывается критерием Рейнольдса, который заключается в сравнении наблюдаемого и критического значений некоторой величины, называемой числомRe.
![]() ,
но так как
,
но так как![]() ,
то
,
то![]() ,
,
где V– скорость движения жидкости,D– диаметр трубы.
Если число Рейнольдса больше или равно некоторому критическому Reкр, течение жидкости становится турбулентным, а приRe<Reкр– течение ламинарное.
Критическое значение числа Рейнольдса определяется геометрией и поверхностными свойствами трубы. Так для гладких цилиндрических труб Reкр= 2300.
Таким образом, критерий Рейнольдса определяет режим течения жидкости. Чем больше вязкость жидкости, тем сильнее надо увеличить скорость для возникновения турбулентности. В широких трубах турбулентное течение возникает легче (при меньшей скорости течения), чем в узких.
Ламинарное течение жидкости по цилиндрическим сосудам. Формула Пуазейля.
Данный вопрос представляет особый интерес для медицины, так как кровеносная система – именно совокупность разветвлённых цилиндрических трубок разного диаметра.
При течении жидкости по трубе скорости частиц в разных точках сечения неодинаковы. Вследствие тормозящего влияния стенок трубы на близлежащие слои скорость частиц жидкости непосредственно у стенок равна нулю. Любой из слоёв вязкой жидкости тормозит движение соседнего слоя, расположенного ближе к оси трубы и ускоряет движение слоя дальше от оси. Поэтому скорость в плоскости сечения непрерывно меняется – от нуля у стенок сосуда до максимально – по оси трубы.
В произвольной точке потока при равномерном течении скорость жидкости зависит от движущей силы, размеров трубы, вязкости жидкости и от расстояния от оси трубы. Можно показать, что при равномерном течении скорость жидкости:
![]() ,
где
,
где
![]() -
разность давлений на концах (торцах)
трубы;
-
разность давлений на концах (торцах)
трубы;
![]() -
длина трубы;R– радиус
трубы;
-
длина трубы;R– радиус
трубы;![]() -
вязкость жидкости;r–
расстояние от оси до точки.
-
вязкость жидкости;r–
расстояние от оси до точки.
Таким образом, график зависимости V(r) представляет собой параболу:
R
 r
r
направление течения жидкости (ось)
«профиль скоростей» - парабола
У стенок трубы r=RиV= 0.
На оси r= 0 и![]()
Объёмная скорость Qжидкости, т.е. объём жидкости, протекающий
через любое сечение трубы в единицу
времени. Измеряется в![]() . При непрерывном теченииQ=const. ВеличинуQопределяетзакон Пуазейля:
. При непрерывном теченииQ=const. ВеличинуQопределяетзакон Пуазейля:
![]() .
.
Согласно закону Пуазейля, при заданных внешних условиях через трубу протекает тем больше жидкости, чем больше радиус трубы и меньше вязкость жидкости.
Формулу Пуазейля можно упростить, используя понятие гидравлического сопротивления:
![]() ,
тогда
,
тогда![]()
Можно также записать формулу в виде,
справедливом для труб переменного
сечения, если заменить выражение
![]() градиентом
давления
градиентом
давления![]() :
:
![]()
Как следует из формулы, при неизменном объёме Qградиент давления больше в трубах меньшего радиуса.
Вязкость и поверхностное натяжение биологических жидкостей.
Биологические жидкости– кровь, лимфа, моча, желудочный сок, желчь, ликвор, слюнная, слёзная и семенная жидкости.
Их вязкость и поверхностное натяжение
зависят от физиологического состояния
организма. В свою очередь, физические
параметры ряда биологических жидкостей
(прежде всего крови) – сами влияют на
состояние организма. Так увеличение
![]() крови способствует тромбообразованию.
Поэтому определение
крови способствует тромбообразованию.
Поэтому определение![]() и
и![]() биологических жидкостей представляет
диагностический интерес – особенно
определение вязкости крови и поверхностного
натяжения мочи.
биологических жидкостей представляет
диагностический интерес – особенно
определение вязкости крови и поверхностного
натяжения мочи.
Среди биологических жидкостей имеются
как ньютоновские, так и неньютоновские
жидкости. Так, ликвор, мочу, лимфу,
сыворотку крови можно считать ньютоновскими
жидкостями. Кровь – жидкость неньютоновская:
белки и форменные элементы крови образуют
пространственные структуры, устойчивость
которых уменьшается при увеличении
градиента скорости течения крови,
разрушение этих структур (деформация
белковых молекул, распад агрегатов
эритроцитов) приводит к уменьшению
![]() .
Поэтому кровь относится к вязкопластичным
жидкостям.
.
Поэтому кровь относится к вязкопластичным
жидкостям.
В норме вязкость крови человека составляет приблизительно 4-5 МПа*с, а поверхностное натяжение мочи приблизительно равно 66 мН/м. При патологии эти параметры изменяются в довольно широких пределах (вязкость от 1,7 до 22,9 МПа*с), что даёт возможность дифференцировать ряд заболеваний, в частности, инфекционных.
Вязкость биологических жидкостей измеряется методом капиллярной вискозиметрии; для измерения вязкости крови используется вискозиметр Гесса. Косвенно о вязкости крови можно судить по скорости оседания эритроцитов (СОЭ). Поверхностное натяжение измеряется методом отрыва капель с помощью прибора – сталагмометра.
Элементы гемодинамики. Модели кровообращения.
Кровеносная система представляет собой совокупность последовательно и параллельно соединённых цилиндрических трубок – сосудов разного диаметра. В норме течение крови по сосудам является, как правило, ламинарным (небольшая турбулентность возникает лишь вблизи сердечных клапанов). Однако под влиянием ряда факторов, приводящих к увеличению числа Рейнольдса, течение в некоторых местах может стать турбулентным.
Наиболее распространённые причины турбулентности:
патологическое уменьшение вязкости крови;
увеличение скорости кровотока сверх некоторой критической вследствие сильного сужения крупных сосудов (как известно, при сохранении непрерывности потока в жидкости – скорость обратно пропорциональна площади сечения
 );
);непосредственное увеличение скорости при напряжённой работе.
При турбулентном течении на образование вихрей тратится дополнительная энергия, и для поддержания кровотока сердце должно совершать большую работу, т.е. на него ложиться дополнительная нагрузка.
Турбулентное течение сопровождается характерным шумом, что может быть использовано для диагностирования заболеваний. С другой стороны, искусственное создание турбулентности лежит в основе наиболее распространённого способа измерения давления – метода Короткова (основная физическая идея: если мускулатура расслаблена, то давление воздуха внутри манжеты соответствует давлению в мягких тканях, соприкасающихся с манжетой; ослабление манжеты => турбулентное течение => шум => систолическое давление => шум уменьшается => диастолическое давление).
Распределение давления и скорости кровотока в разных отделах кровяного русла:
Д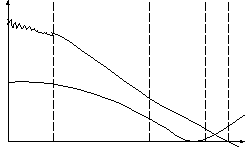 авление
авление
в мм рт ст
120
100
80
скорость60
см/с
40
20
крупные артериолы капилляры вены полая
артерии вена
Сердце - аорта – артерия – артериола – капилляры – венула – вена – полая вена – сердце.
К ламинарному течению крови в принципе применимо уравнение Пуазейля. В то же время для адекватного описания всей системы кровообращения уравнение Пуазейля недостаточно. Действительно:
1) сосуды не жёсткие трубки, а упругие резервуары, их стенки обладают эластичностью;
2) свойства сосудов (упругость) меняются по ходу сосудистого русла;
3) на движение крови оказывают значительное влияние физические свойства эритроцитов (их форма и эластичность их стенок);
4) само движение носит колебательный характер вследствие периодичности функционирования сердца.
Ввиду сложности учёта всех гемодинамических факторов для изучения конкретных закономерностей и определённых участков сосудистого русла используют упрощённые схемы – модели кровообращения. Они бывают гидродинамическими и электрическими.
Гидродинамические и электрические аналоги.
Гидродинамическая величина Электрическая величина
давление р электрический потенциал
![]()
объёмная скорость QЭлектрический токI
Гидравлическое сопротивление XОмическое активное сопротивлениеR
Гидравлическая ёмкость Электрическая ёмкость С
Инерционная индуктивность Электромагнитная индуктивность L
В основе электрических моделей лежит глубокая аналогия между механическими и электрическими явлениями.
Так простейшей электрической моделью системы кровообращения является следующая электрическая цепь:
 D
D
ECR
Здесь источник Eпеременного напряжения – аналог сердца, диодD– сердечного клапана, пропускающего кровь только в одном направлении, конденсатор ёмкостиC– сглаживает колебания силы тока – аналог аорты и крупных артерий, резисторR– аналог периферической сосудистой системы.
В свою очередь, только периферическую
артериальную систему достаточно
адекватно можно описать в рамках
резистивной модели. Действительно,
эластичность стенок микрососудов мала,
и их ёмкостными свойствами можно
пренебречь. В результате система сосудов
заменяется системой параллельно и
последовательно соединённых резисторов,
общее сопротивление которых определяется
по известным правилам. Кровоток в такой
системе может быть реально описан на
основе аналогии уравнения Пуазейля:
![]() и закона Ома для участка цепи:
и закона Ома для участка цепи:![]() .
.
Работа сердца: ударный объём = 60 мл; общий объём 3,6 л; Апрж= 0,2 Алж;Vаорте=0,5 м/с, плотность крови 1,05г/см3, время систолы 0,3 с, давление систолическое = 100 мм рт ст.
![]()
![]()
Работа сердца за сутки: 86,4 КДж.
Мощность сердца за цикл:
![]()
