2.2.2. Мощность и энергия

Мощность, так же как напряжение и ток, можно представить либо числом, либо функцией времени. Мощность, как функция времени p(t), есть произведение периодических функций напря­жения и(t) и тока i(t) одной частоты:

p(t) = и(t) i(t).

При этом частота данной также периодической функции p(t) вдвое выше частоты исходных сигналов (рис. 2.7).

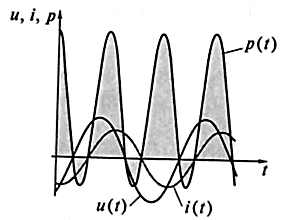
Рис. 2.7.

В самом общем случае усредненная на периоде T активная мо­щность Р (как значение, число) есть интеграл за период T функ­ции p(t) или интеграл произведения функций напряжения и(t) и тока i(t):

.

Графическая иллюстрация поведения мощности p(t) (функции времени) в зависимости от изменения фазового сдвига φ (для си­нусоидальных сигналов) показана на рис. 2.8.

Рис. 2.8. Зависимость активной мощности от угла сдвига фаз: а – φ = 0; б –φ = 60°; в – φ = 90°.

При нулевом значении φ (что соответствовало бы идеальному варианту – чисто активной нагрузке) активная мощность Р мак­симальна, а реактивная мощность Q отсутствует (см. рис. 2.8, а). Чем больше фазовый сдвиг φ, тем хуже со­отношение между активной и реак­тивной составляющими общей мощности, тем ниже эффективность ис­пользования энергии. Например, если представить чисто индуктивную на­грузку (ток отстает от напряжения на φ = 90°), то в этом случае (рис. 2.8, в) активная мощность Р = 0, а реактив­ная Q – максимальна.

Активная мощность тоже может быть функцией времени Р(t). Напри­мер, если несколько потребителей электроэнергии (от одного источника периодически включаются и (или) отключаются (рис. 2.9, а), то, естественно, суммарная активная мощность будет меняться, как показано на рис. 2.9, б.

Рис. 2.3.

Активная энергия, как и другие рассмотренные величины, также может быть представлена функцией времени w(t) (см. рис. 2.9, б). Если известно, как ведет себя функция активной мощности Р(t), и на некоторых интервалах времени t_i ее значения известны и посто­янны, то активную энергию W, потребленную на интервале (t₅…t₁), можно найти как сумму произведений (Р_i t_i ) (см. рис. 2.9, б):

.

В общем случае, если функция активной мощности Р(t) извес­тна, то энергия W, потребленная на некотором интервале (t₁…t₀), определяется так:

.

2.3. Трехфазные электрические цепи

В основе современной электроэнергетики лежат принципы трех­фазного генерирования, передачи, преобразования и потребления электрической энергии.

2.3.1. Напряжения и токи в трехфазной цепи

В трехфазных цепях используются три периодических напряже­ния синусоидального характера одной частоты (50 Гц), которые сдвинуты друг относительно друга на 1/3 периода Т, т.е. на 120°. Временные диаграммы фазных напряжений и токов приведены на рис. 2.11. Первая фаза – А; вторая – В; третья – С.

Наиболее общий случай – четырехпроводное подключение трех­фазной нагрузки (нагрузка типа «звезда») к трехфазной сети – показан на рис. 2.12.

Напряжения между нейтральным проводом N и линейными про­водами (U_A, U_B, U_C) называют фазными (U_ф), а напряжения между линейными проводами U_A, U_B, U_C – линейными (U_л). В случае симметричных цепей соотношения между этими напряжениями: