384 / ТиСУ_Лекции 24_Нелинейные САУ

Лекция __. Нелинейные системы

3. Фазовый метод

Для наглядного представления о процессах, происходящих в нелинейной системе при различных начальных условиях, часто используют фазовый метод, основанный на понятии фазового пространства [1]. Сущность этого метода поясним на примере нелинейной системы третьего порядка, уравнения которой в канонической форме имеют вид:

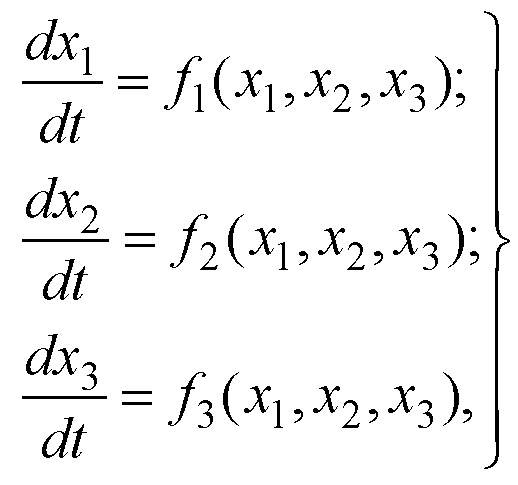(1)

где- нелинейные функции от переменных системы х1, х2 и х3.

Переменныеможно условно принять за координаты некоторой точки M в прямоугольной системе координат (рис. 10).

С течением времени в реальном процессе величины х1, х2, х3 определенным образом изменяются. Это соответствует перемещению точки M по определенной траектории. Эта траектория может служить наглядной геометрической иллюстрацией поведения системы в процессе управления. Точку M принято называть изображающей точкой, ее траекторию - фазовой траекторией, а пространство - фазовым пространством. Семейство фазовых траекторий, построенных для данной системы при различных начальных условиях, называется фазовым портретом системы.

По правым частям уравнений (1) можно судить о направлении движения изображающей точки, а, следовательно, и о поведении соответствующей реальной системы.

Если уравнения составлены в отклонениях от установившегося состояния, то ему будет соответствовать начало координат.

Рис. 10

На практике чаще всего фазовый метод используют при рассмотрении систем второго порядка. В этом случае фазовое пространство двумерно - фазовая плоскость.

Чаще всего в качестве координат фазовой плоскости используют основную переменную х и скорость ее изменения. В дальнейшем мы будем пользоваться именно этими фазовыми переменными. Уравнения при этом будут:

Поделив первое уравнение на второе, получим дифференциальное уравнение траектории на фазовой плоскости:

(2)

Отметим некоторые свойства фазового портрета.

1. Так как призначение х только возрастает, то в верхней фазовой полуплоскости с течением времени изображающая точка движется по фазовой траектории слева направо. Соответственно в нижней полуплоскости движение происходит справа налево. Направление движения на траекториях отмечают стрелками.

2. Ось абсцисс у = О фазовые траектории пересекают под прямым углом сверху вниз в правой и снизу вверх в левой полуплоскостях (за исключением начала координат).

3. Фазовые траектории не пересекаются (за исключением особых точек).

4. Фазовые траектории линейных систем

Пусть система описывается уравнением второго порядка

Введем обозначение для скорости изменения отклонения управляемой величины у = dxjdt. Тогда уравнение системы можно преобразовать к виду

Исключив из этих уравнений время t, разделив первое из них на второе, получим:

Решение этого дифференциального уравнения с различными постоянными интегрирования дает семейство фазовых траекторий (фазовый портрет).

1. корни вещественные отрицательные при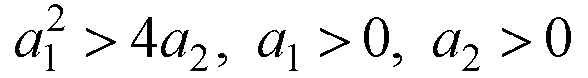(устойчивая система);

2. корни вещественные положительные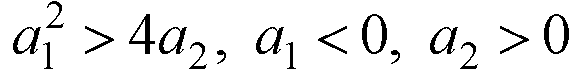(неустойчивая система);

3. корни вещественные и имеют разные знаки при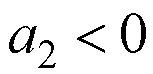(неустойчивая система).

Рассмотрим отдельно различные случаи.

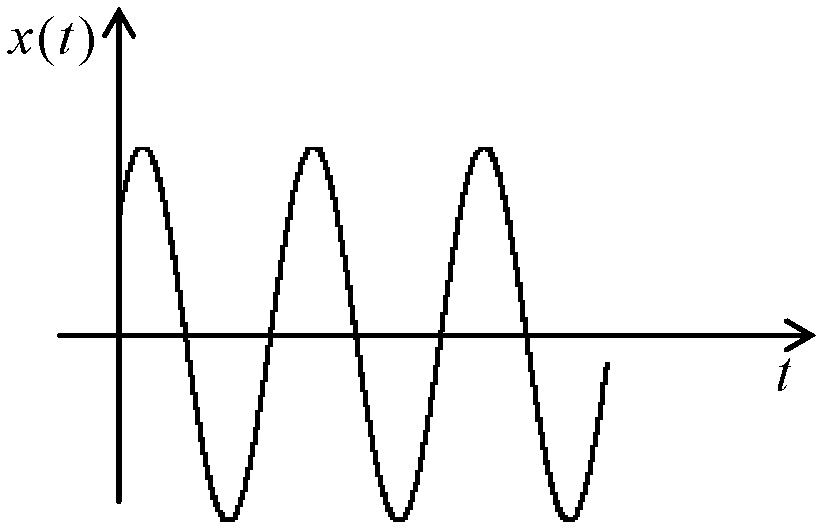
1. В этом случае в системе происходят незатухающие колебания (рис. 11

с постоянной амплитудой А и начальной фазой, которые зависят от начальных условий.

а) б)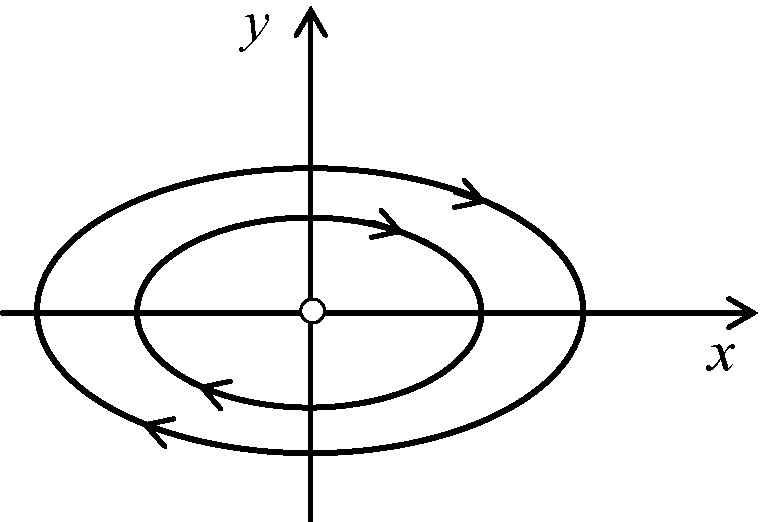

Рис. 11 a)

Для фазовой плоскости эти уравнения являются уравнениями эллипса в параметрической форме. Уравнение эллипса можно получить, интегрируя (3) при

Таким образом, периодическим колебаниям системы соответствует движение изображающей точки по замкнутой кривой (рис. 11 б).

2. В этом случае (комплексные корни с отрицательными вещественными частями) имеют место затухающие колебания (рис. 12 а)

a) 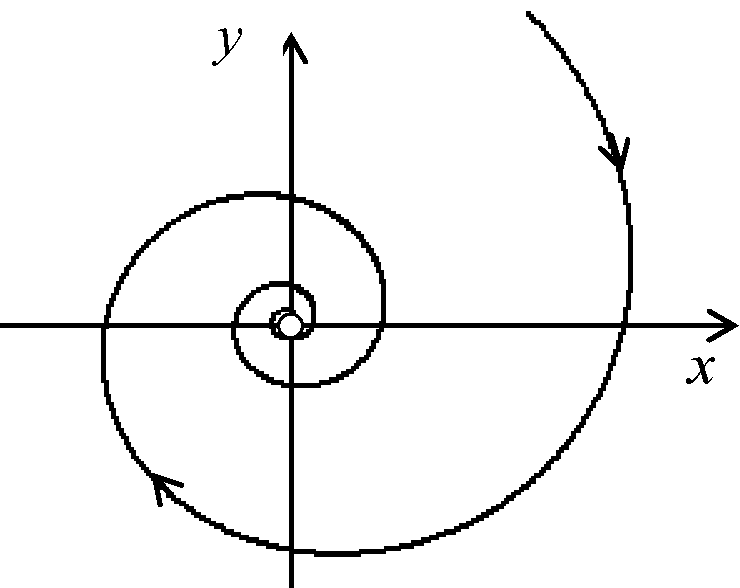б)

Рис. 12

Очевидно, что значения переменных х и y за период колебаний уменьшаются. При этом траектория на фазовой плоскости за один оборот подходит ближе к началу координат. Таким образом, фазовые траектории при затухающих колебаниях выглядят в виде спиралей, сходящихся к началу координат (рис. 12 б).

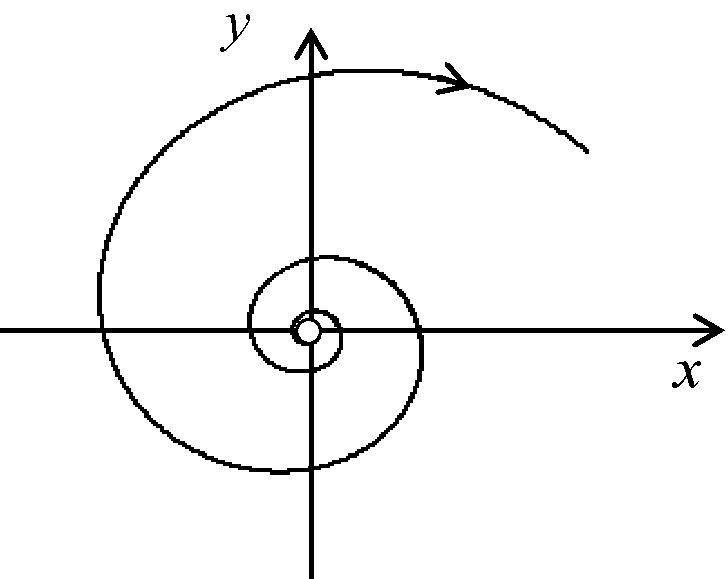
3. Этот случай (комплексные корни с положительными вещественными частями) соответствует расходящимся колебаниям (рис. 13 а). Рассуждая аналогично предыдущему случаю, получим семейство фазовых траекторий тоже в виде спиралей, только изображающая точка будет двигаться по ним не к началу координат, а от него (рис. 13 б).

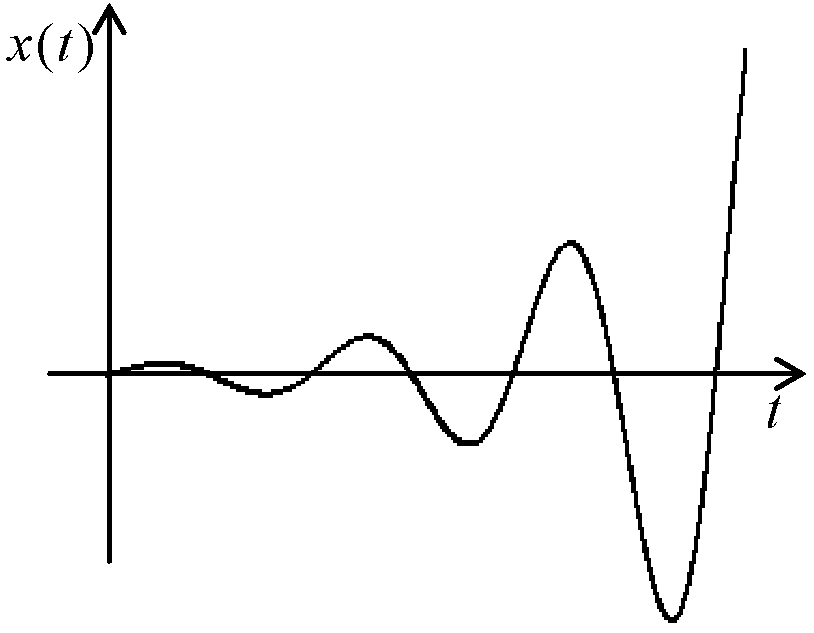
а) б)

Рис. 13

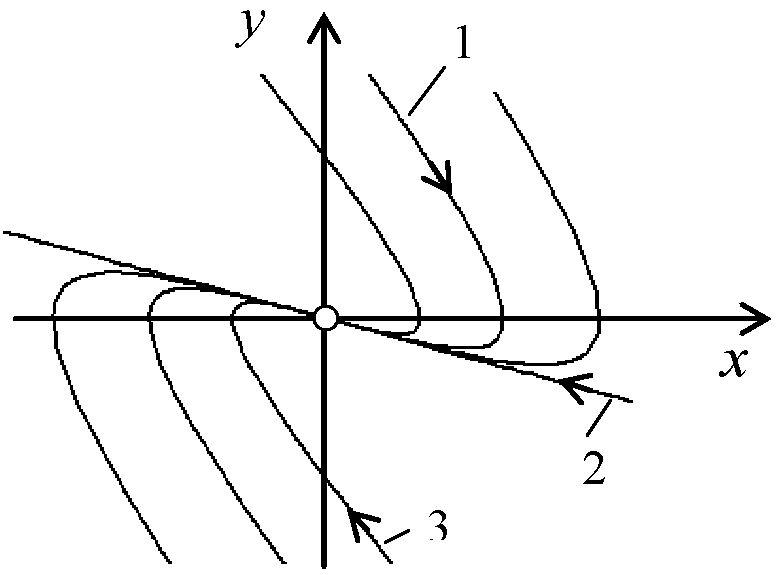
4. Этот случай (вещественные отрицательные корни) соответствует апериодическому процессу.

Переходный процесс представляет собой сумму двух затухающих экспонент. На рис. 14 (а) показаны некоторые реализации таких процессов, фазовые траектории - на рис. 14 (б). Все фазовые траектории вливаются в начало координат фазовой плоскости, то есть изображающая точка стремится к нему асимптотически.

a) б)

Рис. 14

10.2. Построение фазовых траекторий с помощью программы VisSim

3