
2ая методичка МАТАН
.pdf
Преобразовав выражения, получим
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
xt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2t 1 |
|
|
|
1 t |
|
t |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arccos |
|
|
t |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yt |
|
2 1 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
|
1 t 2 |
|
t |
|||||||||||||||||||
Подставим найденные значения в формулу (1.2) и упростим полученное выражение
|
yt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t 1 2 |
|
|
|
|
|
yx |
|
2 t 1 t arccos t 1 |
|
1 t |
t |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xt |
|
4 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
|
t |
1 t |
1 t |
|
|
||||||||||||||||
2t 1 2
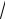 t
t 
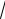 1 t arccos
1 t arccos
 t 1 .
t 1 .
|
|
2t 1 2 |
|
|
|
|
|
2 1 t |
|
1 . |
|
|
|
|
|
|
arccos |
|
|||
Ответ: yx |
t |
1 |
t |
t |
||||||
|
|
|
|
|
|
|
|
|||
2 |
|
1 t |
|
|||||||
|
|
|
|
|
|
|||||
Задача 1.3. Найти производную данной функции указанного порядка в заданной точке.
Данные к условию задачи, соответствующие вариантам:
1) |
y x 1 ln x 1, |
yIII (2) ?; |
12) |
y x 3 ln x 3 , |
yIII 4 ?; |
||||||||||||||||||||||||||||||||||||
2) |
y x2 ln2 x, |
|
yIII 1 ?; |
|
|
|
|
|
|
13) |
y x3 ln2 x, |
yIII 1 ?; |
|
|
|||||||||||||||||||||||||||
3) |
y xcosx2, |
|
yIII ?; |
|
|
|
|
|
|
14) |
y |
1 |
sin2x, |
yIII ?; |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
ln x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
4) |
y |
|
, |
|
yIII 2 ?; |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
15) |
y x 4 ln x 4 , |
yIII 3 ?; |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
5) y |
log |
2 |
x |
yIII 2 ?; |
|
|
|
|
|
|
|
16) |
y 3x 7 3 x, |
yIII 1 ?; |
|||||||||||||||||||||||||||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
ln 2x 5 |
|
|
|
|
|
|
||||||||||||||||
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
17) |
y |
|
, |
|
yIII 2 ?; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
y 4x3 |
|
5 e2x 1, |
yIII |
|
|
|
|
|
2x 5 |
|
|
|
|
|
||||||||||||||||||||||||||
6) |
|
|
|
|
|
?; |
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
18) |
y e |
|
sin2x, |
|
yIII ?; |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
III |
|
|
|
|
|
|
|
|
|
|
lnx |
|
|
|
|
|
|
|
|
|||||||||||
7) |
y |
|
|
|
x sin 5x |
|
|
, |
y |
|
|
|
|
?; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
19) |
y |
|
|
|
|
, yIII 1 ?; |
|
|
||||||||||
|
|
|
|
|
lnx |
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
|
|||||||||||||||||||||
8) |
y |
, |
|
|
yIII 1 ?; |
|
|
|
|
|
|
|
|
20) |
y 1 3x ln 1 3x , |
yIII 0 ?; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
x2 |
|
|
|
|
|
|
yIII 1 ?; |
|
|
|
|
|
|
|
y x2 |
3x e3x 2, |
|
2 |
||||||||||||||||||
9) |
y 2xln2 x, |
|
|
|
|
|
|
|
21) |
yIII |
|
?; |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
y 1 x2 arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||||||
|
yIII |
|
?; |
|
y 5x 8 2 x, |
yIII 1 ?; |
|||||||||||||||||||||||||||||||||||
10) |
|
|
|
|
22) |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
ln x 2 |
|
|
yIII 3 ?; |
|
|
||||||||
11) |
y 4x 3 2 x, |
yIII 1 ?; |
23) |
y |
, |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
||||
10
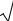
|
y |
lnx |
, |
|
yIII 1 ?; |
|
y x3 |
3 e4x 3, |
|
|
3 |
|
||||||||||||||||
24) |
|
|
|
|
28) |
yIII |
|
|
|
|
?; |
|||||||||||||||||
x3 |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
y 1 x x2 e 2 |
, yIII 1 ?; |
|
|
|
|
|
|||||||||||||||||||||
25) |
29) |
y e2x |
sin |
|
3x |
, yIII |
|
|
|
|
?; |
|||||||||||||||||
3 |
|
|
|
|||||||||||||||||||||||||
26) |
y |
ln 3 x |
, |
yIII 2 ?; |
|
|
log3 x |
|
|
|
|
|
3 |
|
||||||||||||||
|
|
|
yIII 3 ?. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
3 x |
|
|
|
|
|
yIII 0 ?; |
30) |
y |
, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
27) |
y 2x3 1 cosx, |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Пример 1.3 |
|
|
|
|
|
|
|
3x 2 e2x 3 |
|
|
|
|
|
|
|
|
|||||||||||
|
Найти производную функции y x2 |
третьего порядка в |
||||||||||||||||||||||||||
точке x |
0 |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Сначала найдем производную первого порядка от заданной функции |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
y x2 |
|
x2 3x 2 e2x |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
3x 2 e2x 3 |
3 |
|
|
|
|
|
|
|||||||||||||
2x 3 e2x 3 x2 3x 2 2e2x 3 e2x 3 2x2 8x 7 .
Для того чтобы вычислить производную второго порядка, нужно найти производную от производной первого порядка. Таким образом,
|
y |
|
|
|
|
|
|
|
|
|
|
7 e2x 3 2x2 |
|
|
|
|
|
|
|||||||
|
y |
e2x 3 2x2 8x |
8x 7 |
|
|
|
|
|
|||||||||||||||||
2e2x 3 2x2 8x 7 e2x 3 4x 8 e2x 3 4x2 20x 22 . |
|
|
|
|
|||||||||||||||||||||
Тогда производная третьего порядка будет иметь вид |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
20x 22 e2x 3 4x2 |
|
|
|
|
|
|
|||||||||
y y |
|
e2x 3 4x2 |
20x 22 |
|
|
|
|
||||||||||||||||||
2e2x 3 4x2 20x 22 e2x 3 8x 20 e2x 3 8x2 48x 64 . |
|
|
|
||||||||||||||||||||||
В полученное выражение вместо переменной подставим значение |
x |
0 |
|
3 |
и |
||||||||||||||||||||
|
|||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
3 |
3 |
|
3 2 |
|
3 |
|
|
|
|
18 72 64 154. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
e |
|
2 |
|
|
|
8 |
|
|
48 |
|
64 |
|
e |
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||||||||||||
y |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 154.
Задача 1.4. Вычислить предел функции, воспользовавшись правилом Лопиталя.
Данные к условию задачи, соответствующие вариантам:
1) lim |
5ln x x |
|
2) lim |
35x 27x |
|
3) lim |
ln 2x 5 |
|||
|
; |
|
; |
|
|
|
; |
|||
|
|
3 |
|
|
||||||
x2 1 |
|
|||||||||
x |
|
x 0 arcsin2x x |
|
x |
8x 3 |
|||||
11

4) lim e3x e 2x x 0 2arcsinx sinx
5)lim x3 1 ;
x1ln x
6) lim |
e5x e3x |
|
|
; |
|
|
||
x 0 sin2x sinx
7)lim ln x 1 ;
x4
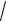 2x 3
2x 3
8) lim |
e2x e3x |
; |
|
||
x 0 arctgx x2 |
|
|
9)lim 4 ;
x3x x4
10) lim e4x e 2x
x 0 2arctgx sinx
1
11) lim 3x ex ;
x 0 1 ln x
12) lime7x e 2x ;
x 0 sinx 2x
Пример 1.4
|
lim |
ln x2 3 |
||||||
; 13) |
|
|
|
|
|
; |
||
|
|
|
|
|
||||
|
x 2 x2 x 2 |
|||||||
|
lim |
4x |
27x |
|||||
14) |
|
|
|
|
; |
|
||
|
|
|
|
|
||||
|
x 0 tg3x x |
|||||||
|
lim |
|
4ln x x |
|||||
15) |
|
|
|
; |
|
|||
|
|
|
|
|||||
|
x 0 |
|
|
x 1 |
||||
16) |
lim |
|
|
102x 7 x |
||||
|
|
|
|
|
|
|
||
x 0 2tgx arctgx
17) lim |
x3 |
8 |
; |
|
|
|
|
||
x 2 ln x 1 |
|
|||
18)lim 5ln x ;
xx 1
; 19) |
lim |
e4x |
e2x |
|
|
|
; |
||
|
|
|||
|
x 0 2tgx sinx |
|||
20) |
lim |
32x 7x |
||
|
|
|
||
x 0 arcsin3x 5x
21)lim 2x 1 ;
xx5 x4
|
lim |
6ln x |
x2 |
|
|
|
|||||
22) |
|
|
; |
|
|
||||||
|
|
||||||||||
|
x 0 x2 |
1 |
|
|
|
||||||
23) |
lim |
|
x3 |
8 |
; |
|
|
||||
|
|
|
|
|
|
|
|||||
|
x 2 ln x 1 |
|
|
|
|||||||
24) |
lim |
|
|
ex e3x |
|
|
; |
||||
|
|
|
|
|
|
|
|||||
|
x 0sin3x tg2x |
||||||||||
; 25) |
lim |
|
|
|
9x 23x |
|
; |
||||
|
|
|
|
|
|
||||||
x 0 arctg2x 7x
26)lim 2 x x3 ;
x 5
27)lim35x 2 7x ;
x 0 |
2x tgx |
|
28) lim |
ln x2 |
|
|
; |
|
|
||
x 1 x2 3x 4
;29) lim e2x ex ;
x 0 x tgx2
30) lim |
23x 32x |
|
|
. |
|
|
||
x 0 x arcsinx3
Вычислить предел функции, воспользовавшись правилом Лопиталя
lim 5x2 7x.
x e2x 1
Решение
При непосредственном вычислении заданного предела получаем неопределен-
ность вида , следовательно, можно использовать правило Лопиталя для вы-
числения предела функции, т.е.
|
5x2 7x |
|
|
|
|
5x2 |
|
|
|
10x 7 |
|
|
|||||||
lim |
|
|
lim |
7x |
|
lim |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
e |
2x 1 |
|
|
|
|
2x 1 |
|
||||||||||||
x |
|
|
|
|
|
x |
e2x 1 |
|
x 2e |
|
|
|
|
||||||
Поскольку снова получили неопределенность вида , то еще раз восполь-
зуемся правилом Лопиталя
12
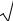
|
10x 7 |
|
|
|
|
10x |
|
|
|
10 |
|
10 |
|
|||||||
lim |
|
|
lim |
7 |
|
lim |
|
0. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2x 1 |
|
|
|
2x 1 |
|
|||||||||||||
x 2e |
|
|
|
|
|
x 2e2x 1 |
|
x 4e |
|
|
|
|
|
|||||||
Ответ: 0.
Задача 1.5. Найти наибольшее и наименьшее значение функции y f x
на отрезке a;b .
Данные к условию задачи, соответствующие вариантам:
1) f x |
|
|
|
|
1 |
|
|
|
|
, |
|
|
|
|
|
|
|
1 |
; |
1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||||||||
x |
2 |
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||
2) f x tg x |
x, |
|
|
|
|
; |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
; |
|
|||||||||||||||||||||||||||||||
4 |
|
4 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||||||||
3) |
f x |
|
x3 |
x2 6x 7, |
1;5 ; |
|||||||||||||||||||||||||||||||||
|
|
|
|
2 |
||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4) |
f x |
1 |
|
x3 2x2 3, |
|
|
|
1;2 ; |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2;2 ; |
||||||||||||||
5) |
f x x4 8x2 3, |
|
|
|
||||||||||||||||||||||||||||||||||
6) |
f x |
1 |
|
x3 |
7 |
x2 12x 1, |
1;5 ; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0;6 ; |
|||||||||||
7) |
f x x3 9x2 15x 3, |
|||||||||||||||||||||||||||||||||||||
8) |
f x |
1 |
x4 2x2 5x, |
3;4 ; |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3;5 ; |
||||||||
9) |
f x 2x3 3x2 3x, |
|||||||||||||||||||||||||||||||||||||
10) |
f x x3 |
3x 2, |
|
|
|
2;3 ; |
||||||||||||||||||||||||||||||||
11) |
f x 2x3 3x2 6, |
|
3;2 ; |
|||||||||||||||||||||||||||||||||||
12) |
f x |
|
|
|
|
|
|
|
|
x |
|
, |
|
3;3 ; |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
|
|
0;2e ; |
|||||||||||||||||||||||
13) |
f x x ln x 1, |
|
||||||||||||||||||||||||||||||||||||
14) |
f x |
|
|
|
|
|
|
8x |
|
, |
3;4 ; |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 4 |
|
|
0;4 ; |
|
|||||||||||||||||||||||
15) |
f x 2 |
|
|
|
|
|
x, |
|
||||||||||||||||||||||||||||||
|
|
|
x |
|
||||||||||||||||||||||||||||||||||
16) |
f x x4 |
2x2 |
4, |
|
|
|
2;2 ; |
|||||||||||||||||||||||||||||||
17) |
f x |
x |
|
5 |
, |
6;6 ; |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
13
18) |
f x |
x3 |
2x2 3x 1, |
0; 4 ; |
||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
3 |
|
|
|
|
|
0;2 ; |
|
|
|
|
||||||||
19) |
f x sin2x, |
|
|
|
|
|
||||||||||||||
20) |
f x |
|
|
x3 |
|
|
x2, |
|
3;1 ; |
|
|
|||||||||
3 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4;1 ; |
|
||||||||
21) |
f x x3 6x2 |
9x, |
|
|||||||||||||||||
22) |
f x |
|
x4 |
|
2x2, |
|
3;3 ; |
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
4 |
|
|
|
|
|
|
1;e ; |
|
|
|
|
|||||||
23) |
f x x ln x, |
|
|
|
|
|
|
|||||||||||||
24) |
f x 2x3 3x2, |
|
2;2 ; |
|
||||||||||||||||
|
f x 2x cos 2x, |
|
|
3 |
|
|
||||||||||||||
25) |
|
|
; |
; |
||||||||||||||||
|
||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
5 |
|
|
|
|
4 |
|
|
|||
26) |
f x |
x3 |
x2 |
6x 7, 1;4 ; |
||||||||||||||||
|
2 |
|||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
27) |
f x |
|
|
|
|
8x |
|
, |
|
4;3 ; |
|
|
||||||||
|
|
|
x2 4 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
0;2 ; |
|
|
|||||||||||
28) |
f x cos2x, |
|
|
|
|
|||||||||||||||
29) |
f x x4 |
3x2 4, |
4; 4 ; |
|
||||||||||||||||
30) |
f x |
|
|
|
|
6x |
|
, |
|
4;4 . |
|
|
||||||||
|
|
|
x2 9 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 1.5
Найти наибольшее и наименьшее значение функции f x sin2x 1 на отрезке ;3 .
Решение
Функция f x sin2x 1 определена на заданном отрезке. Вычислим первую
производную
f x sin2x 1 2sinxcosx sin2x.
Найдем точки, в которых производная функции равна нулю f x 0 при условии, что sin2x 0,
откуда, решив тригонометрическое уравнение, получаем множество корней
x |
n |
, |
n N. |
|
|||
2 |
|
|
|
Выберем из полученной серии корней те, которые принадлежат отрезку
;2 :
14
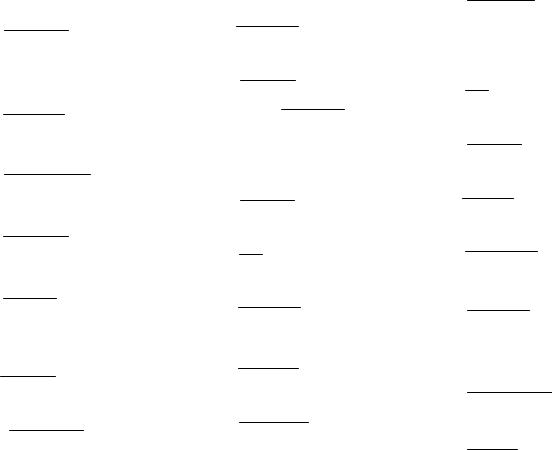
n 2, |
x ; |
n 3, |
x |
3 |
; |
n 4, |
x 2 . |
|
|||||||
|
|
|
2 |
|
|
|
|
Определим значение функции в найденных точках и на концах заданного отрезка (в нашем примере эти значения совпали) и выберем среди них наибольшее и наименьшее
f sin2 1 1, |
|
|
|
3 |
|
3 |
|
f 2 sin22 1 1, |
||||
|
|
|
f |
|
sin2 |
|
|
1 2, |
||||
|
|
|
|
2 |
||||||||
следовательно, |
|
|
|
|
|
2 |
|
|
|
|||
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
f |
|
|
|
|
2 – наибольшее значение функции, |
|||||||
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
f f 2 1 – наименьшее значение функции. |
||||||||||||
Ответ: fнаиб f |
3 |
2, |
fнаим |
f f 2 1. |
||||||||
|
|
|
|
|
||||||||
|
2 |
|||||||||||
р;2р |
|
|
|
|
р;2р |
|
|
|
|
|||
Задача 1.6. Провести полное исследование функции и построить ее график.
Данные к условию задачи, соответствующие вариантам:
1)y x e x ;
2)y x lnx; x
3)y x2 e2x ;
x3
4)y x 1 2 ;
2
5) y ex x 1 ;
x 1 3
6) y x 2 2 ;
7) y x2 1;
x2 4
8) y x arctg3x;
9) y 4x 1;
x2 4
10) y 2x lnx;
x
11)y x arctgx;
12)y 2 lnx ;
x
13)y x2 4; ex
14)y 1 3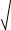 x 1 2 ;
x 1 2 ;
15)y x2 e x;
16)y 3x 4; x2 1
17)y 2 3x; x2
1 2x
18) y 1 x 2 ;
19) y 4x2 1;
x2 9
20) y 1 2lnx ;
2x
32x
21)y x 2 2 ;
22)y x3 e x;
23)y 1 2x;
x2
24)y x2 4;
x2 1
25)y 1 2x ;
ex
26) y 2x lnx;
3x
x 1 3
27)y x2 1 ;
28)y 2x e 2x;
3
29) y ex x 1 ;
30) y 2x 1.
ex
15

Пример 1.6
Провести полное исследование функции y x3 e2x и построить ее гра-
фик.
Решение
Проведем полное исследование функции по следующей схеме: 1. Область определения.
D y ; .
2. Четность и нечетность.
Область определения функции симметрична относительно нуля. Найдем
y x
y x x 3 e2 x x3e 2x .
Поскольку y x y x , то функция не является четной, кроме того, y x y x , значит, функция не является нечетной.
– функция общего вида.
3. Периодичность.
Функция не является периодичной, т.к.
x3 e2x x T 3e2 x T ,
таким образом,
y x y x T ,
для любого значения T, отличного от нуля.
4. Точки пересечения с осями координат и промежутки знакопостоянства. С осью Ox: y 0, т.е. необходимо решить уравнение
x3 e2x 0,
откуда находим,
x 0.
Точка пересечения с осью Ox: 0;0 .
С осью Oy: x 0, т.е. в уравнение функции вместо аргумента подставим значение ноль и получим
y 03 e2x 0.
Точка пересечения с осью Oy: 0;0 .
Отметим на числовой прямой найденную точку пересечения с осью Ox (рис. 1), в каждом из полученных промежутков проверим знак функции
– |
+ |
х |
0
Рис. 1
y 1 1 3 e2 1 e 2 0,
16

y 1 13 e21 e2 0.
Следовательно,
y 0 при x ;0 ; y 0 при x 0; .
5. Промежутки возрастания и убывания, экстремумы функции и точки экстремума.
Найдем производную первого порядка исследуемой функции
y x3 e2x x3 e2x x3 e2x 3x2e2x x3 2e2x e2x 3x2 2x3 .
Найдем точки, в которых производная обращается в ноль, и отметим их на числовой прямой (рис. 2)
e2x 3x2 2x3 0, e2x 0, 3x2 2x3 0, x2(3 2x) 0,
|
x 0, |
x |
3 |
. |
|
|
|
|
|||
|
|
2 |
|
|
|
– |
min |
+ |
|
||
+ |
х |
||||
3 0
0
2
Рис. 2
Проверим знак первой производной функции в каждом из полученных промежутков
y 2 e2 2 3 2 2 2 2 3 4e 4 0, y 1 e2 1 3 1 2 2 1 3 e 2 0, y 1 e2 1 3 12 2 13 5e2 0.
Если значение производной функции на промежутке отрицательно, то функция убывает, если положительно, то функция возрастает. Точка, в которой производная меняет знак, является точкой экстремума. Следовательно,
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
функция убывает при x |
; |
|
|
, |
|
|||||||||||
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
функция возрастает при x |
|
3 |
|
|
|
|
|
|||||||||
|
|
; |
, |
|||||||||||||
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
min |
|
3 |
, y |
min |
|
27 |
e 3. |
|
|
|
|
||||
|
|
|
|
|
|
|||||||||||
|
2 |
|
8 |
|
|
|
|
|
|
|
||||||
6. Промежутки выпуклости функции и точки перегиба. Найдем производную второго порядка исследуемой функции
y e2x 3x2 2x3 e2x 3x2 2x3 e2x 3x2 2x3
17
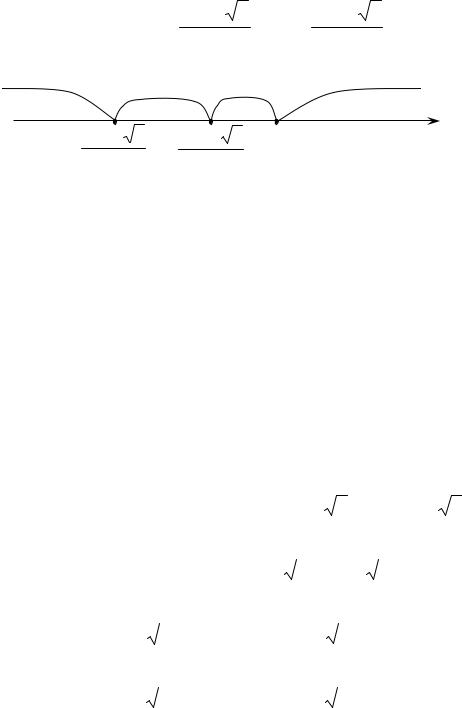
2e2x 3x2 2x3 e2x 6x 6x2 2e2x 2x3 6x2 3x .
Найдем точки, в которых вторая производная обращается в ноль, и отметим их на числовой прямой (рис. 3)
2e2x 2x3 6x2 3x 0, 2e2x 0, 2x3 6x2 3x 0, x(2x2 6x 3) 0,
x 0, |
x 3 3, |
x 3 3 . |
|
|
|
2 |
|
2 |
|
– |
+ |
– |
+ |
х |
3 3 |
3 |
3 |
0 |
|
2 2
Рис. 3
Проверим знак производной второго порядка функции в каждом из полученных промежутков
|
|
|
|
|
|
2 3 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 3 6 3 |
3 3 2e |
|
|
9 0, |
|||||||||||||||||||||
|
y 3 2e |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 1 |
6 1 |
3 1 2e |
|
|
1 0, |
|
||||||||||||||||||
|
|
|
y 1 2e |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
3 |
|
|
1 |
2 |
|
|
1 |
|
|
|
|
|
|
1 |
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
2e |
|
|
|
2 |
|
2 |
|
|
6 |
|
|
|
|
3 |
|
|
|
|
2e |
1 |
|
|
|
0, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
y |
2 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
3 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 1 6 1 3 1 2e 11 0. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
y |
|
1 2e |
|
|
|
|
|
|
||||||||||||||||||||||||
Если значение второй производной функции на промежутке отрицательно, то функция выпукла вверх, если положительно, то функция выпукла вниз. Точка, в которой вторая производная меняет знак, является точкой перегиба. Следовательно,
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
3 |
3 |
||||||||||||
функция выпукла вверх при x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
; |
|
|
|
|
|
|
|
|
|
|
|
;0 , |
||||||||||||||
|
2 |
|
|
|
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функция выпукла вниз при x |
3 |
|
3 |
; |
3 |
|
3 |
0; , |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|||||||||||
xперег |
|
|
yперег |
|
|
|
0,12, |
|
|
|||||||||||||||||
|
, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y |
2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
||||||||
xперег |
|
|
|
yперег |
|
|
|
|
0,07, |
|
|
|||||||||||||||
|
, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
xперег 0, yперег y 0 0.
18

7. Асимптоты.
Функция определена на всей числовой прямой, значит вертикальных асимптот нет.
Наклонные асимптоты находим в виде (1.3)
где |
y kx b, |
(1.3) |
|||
|
f x |
|
|
||
k lim |
, |
(1.4) |
|||
|
|||||
|
x |
x |
|
||
b |
lim f x kx . |
(1.5) |
|||
|
x |
|
|
|
|
Если значения пределов (1.4) и (1.5) существуют и конечны, то у функции есть наклонные асимптоты. Если значение предела (1.4) равно нулю, значение предела (1.5) существует и конечно, то из формулы (1.3) получаем уравнение горизонтальной асимптоты (1.6)
y b. |
(1.6) |
В формулу (1.4) подставим исследуемую функцию и найдем значение k
k lim |
x3e |
2x |
|
lim x2e2x 0 lim |
x2 |
|
|
|
, |
|||
|
|
|
|
|
|
|||||||
x |
x |
|
|
x |
x e |
2x |
|
|
|
|||
|
|
|
|
|
|
|
||||||
после проведенных преобразований можно использовать правило Лопиталя для вычисления предела
k lim |
|
x2 |
|
|
|
lim |
|
|
2x |
|
|
|
|
lim |
|
|
2 |
|
|
|
|
|
|
2 |
0. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2x |
|
|
|
|
|
2x |
|
|
|
|
|
2x |
|
|
|
|||||||||||||||||||||||||
x e |
|
|
|
|
|
x 2e |
|
|
|
|
|
|
x 4e |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Найдем значение b, воспользовавшись формулой (1.5) |
|
|
|
|
x3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
b lim x3e2x 0 x lim x3e2x 0 lim |
|
|
|
|
|
|
|
, |
||||||||||||||||||||||||||||||||||
|
|
|
|
2x |
|
|
||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x e |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
вычислим предел с помощью правила Лопиталя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
b lim |
|
|
|
x3 |
|
|
|
|
|
|
3x2 |
|
|
|
|
|
|
|
6x |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2x |
|
|
|
|
|
2x |
|
|
|
|
|
2x |
|
||||||||||||||||||||||||||
x e |
|
|
|
|
|
x 2e |
|
|
|
|
|
x 4e |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
66
lim 8e 2x 0.
Поскольку значение k равно нулю, то, подставив найденное значение b в формулу (1.6), получим уравнение горизонтальной асимптоты функции при
x
y 0.
Аналогично определим наклонную асимптоту x . Найдем коэффициент
k
k lim |
x3e |
2x |
|
lim x2e2x , |
x |
|
|||
x |
|
|
x |
19
