Analiticheskaya_geometria
.doc
22)
;
23)
;
24)
;
25)
;
26)
;
27)
;
28)
;
29)
;
30)
.
Пример 5.3
Законы спроса и
предложения на некоторый товар
соответственно определяются уравнениями
,
,
где p
– цена на товар, q
– количество товара. Предполагается,
что спрос определяется только ценой
товара на рынке pС,
а предложение – только ценой pS,
получаемой поставщиками. Необходимо
а) определить точку рыночного равновесия;
б) точку равновесия
после введения налога
.
Определить увеличение цены и уменьшение
равновесного объема продаж;
в) найти субсидию
s,
которая приведет к увеличению объема
продаж на
ед. относительно
изначального (определенного в пункте
а));
г) найти новую
точку равновесия и доход правительства
при введении налога, пропорционального
цене и равного
;
д) определить,
сколько денег будет израсходовано
правительством на скупку излишка при
установлении минимальной цены,
.
Решение
а)
Находим точку рыночного равновесия из
условия
(рис. 11):
,
,
;
.
Ответ:
– точка рыночного равновесия.
б)
Если введен налог
,
то система уравнений для определения
точки равновесия примет вид
.
Используя соотношение
между ценой на рынке
и ценой
,
получаемой поставщиками, имеем следующие
выражения для определения точки рыночного
равновесия
,
.
Откуда находим новую точку рыночного равновесия
(рис. 12).
Следовательно,
после введения налога равновесная цена
увеличилась на
ден. ед., а равновесный объем уменьшился
на
ед.
Ответ:
– точка равновесия после введения
налога
,
равновесная цена увеличилась на
ден. ед., равновесный объем уменьшился
на
ед.
|
Р |
Р |
ис.
11
ис.
12
в) Если предоставляется субсидия, то система для определения точки равновесия имеет вид
.
Новый объем продаж
равен
единицы, подставляем
в систему, находим
.
Ответ: субсидия, которая приведет к увеличению объема продаж на 2 ед. относительно изначального, должна быть равна 6 ден. ед. (рис. 13).
г) Если налог составляет 15%, то вся рыночная цена составляет 115%, из них 100% получают поставщики товара, 15% – государство. Итак, поставщики получают
.
Таким образом, система для определения новой точки рыночного равновесия имеет вид
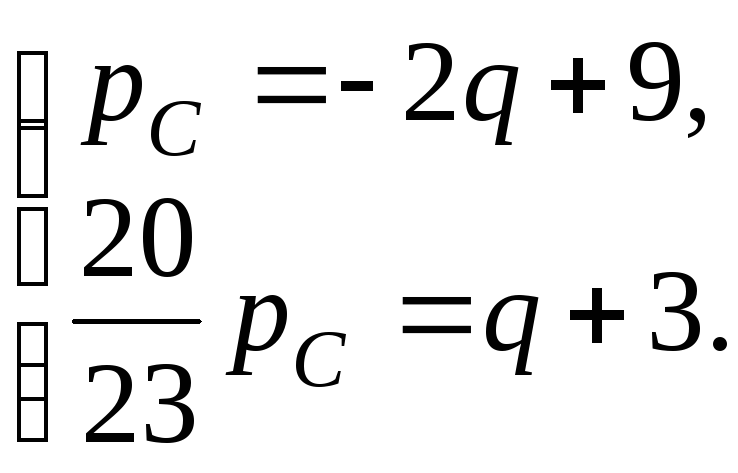
Решая эту систему, находим новую точку рыночного равновесия
,
при этом доход правительства R будет равен
.
На рис. 14 доход правительства соответствует площади заштрихованного прямоугольника.
|
Р |
Р |
ис.
13
ис.
14
Ответ:
– точка равновесия,
ден. ед. –
доход правительства при введении налога,
пропорционального цене и равного 15%.
д) Если установлена минимальная цена, то из уравнений спроса и предложения можно найти объемы спроса и предложения, соответствующие данной цене. Если минимальная цена выше равновесной цены, то объем предложения превышает объем спроса, тогда разницу между ними скупает правительство.
При
находим
.
Таким образом, затраты правительства составят
.
На рис. 15 затраты правительства соответствуют площади заштрихованного прямоугольника.
Ответ: правительством будет израсходовано 9 ден. ед. на скупку излишка при установлении минимальной цены, равной 6.
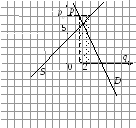
Рис. 15
Задача 5.4. Даны четыре точки A, B, С, D. Необходимо
а) написать уравнения плоскостей ABC и ВCD;
б) написать уравнения прямых BC и AD;
в) найти расстояние от точки А до плоскости ВCD.
Данные к условию задачи, соответствующие вариантам:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
.
Пример 5.4
Даны четыре точки
,
,
,
.
Необходимо
а) написать уравнения плоскостей ABC и ВCD;
б) написать уравнения прямых BC и AD;
в) найти расстояние от точки А до плоскости ВCD.
Решение
а) Для плоскостей, уравнения которых необходимо написать, известны координаты точек, принадлежащих этим плоскостям, значит, для составления уравнений воспользуемся формулой уравнения плоскости, проходящей через три заданные точки
|
|
(5.6) |
,
где
,
,
– координаты точек, принадлежащих
искомой плоскости.
Подставляя координаты соответствующих каждой плоскости точек в формулу (5.6), получаем
,
.
Раскрывая определитель и упрощая полученные выражения, приводим уравнения плоскостей к общему виду
,
,
.
,
,
,
.
Ответ:
,
.
б)
Уравнения
и
составим как уравнения прямых, проходящих
через две заданные точки
|
|
(5.7) |
,
где
,
– координаты точек, принадлежащих
искомым прямым.
Таким образом, подставляя координаты соответствующих прямым точек в формулу (5.7), получаем
,
.
,
.
Ответ:
,
.
в)
Расстояние
от точки
до плоскости
найдем по следующей формуле
|
|
(5.8) |
,
где
– уравнение плоскости
,
– координаты точки
.
Уравнение плоскости
было найдено ранее в пункте а),
координаты точки
даны в условии задачи
,
,
подставляем эти данные в формулу (5.8)
.
Ответ:
.
Задача 5.5. Даны
уравнения плоскостей
и
,
а также уравнения прямых
и
.
Определить
а) взаимное
расположение плоскостей
и
и найти угол между ними;
б) взаимное
расположение прямых
и
,
найти угол между ними;
в) взаимное
расположение прямой
и плоскости
,
найти угол между прямой
и плоскостью
.
В том случае, если прямая и плоскость
параллельны, найти расстояние между
ними; в случае, если прямая и плоскость
пересекаются (в частности перпендикулярны)
– найти точку их пересечения.
Данные к условию задачи, соответствующие вариантам:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
Пример 5.5
Даны уравнения
плоскостей
и
,
а также уравнения прямых
и
.
Определить
а) взаимное
расположение плоскостей
и
,
найти угол между ними;
б) взаимное
расположение прямых
и
и угол между ними;
в) взаимное
расположение прямой
и плоскости
,
найти угол между ними. В том случае, если
прямая и плоскость параллельны, найти
расстояние между
и
;
в случае, если прямая и плоскость
пересекаются (в частности перпендикулярны)
– найти точку их пересечения.
Решение
а)
Запишем координаты векторов нормали
и
соответственно плоскостей
и
(коэффициенты при переменных в уравнениях
данных плоскостей)
;
.
Определим взаимное
расположение векторов
и
,
т.к. если
,
то
,
если
,
то
,
иначе
.
координаты векторов
нормали заданных плоскостей не
пропорциональны, следовательно,
и
не параллельны,
скалярное
произведение векторов нормали заданных
плоскостей не равно нулю, следовательно,
и
не перпендикулярны, таким образом,
плоскости пересекаются под углом
по прямой
.
Найдем угол
между плоскостями
и
.
Ответ:
,
.
б)
Запишем координаты направляющих векторов
и
соответственно прямых
и
(знаменатели в уравнениях данных прямых)