2,2 % Со2; 13,6 % со; 18,6 % н2; 10,9 % н2о; 54,7 % n2.

Равновесное давление кислорода находим из выражения для константы равновесия реакции (1):

атм,

где 2,6∙10¹⁰ = при 1600 К (см. пример 1.8).

Равновесное давление метана находим из выражения для константы равновесия реакции (3). Константу равновес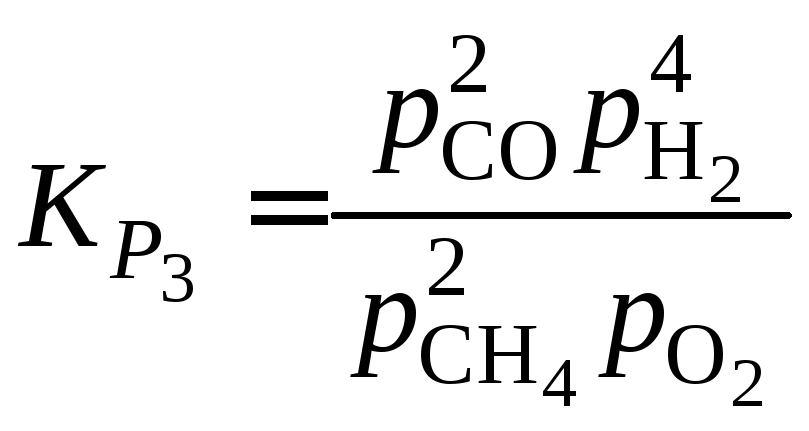ия вычисляем из уравнения (Дж) (см. пример 1.2). При 1600 К она равна .Тогда

атм.

Следует сделать вывод, что, действительно, ивесьма малы.

Пример 1.10. Проба газа, взятая из печи при 1000 К иР= 1,1 атм, по результатам анализа содержит, % (об): 18,5 % СО₂, 20,5 % СО, 14 % Н₂, 2,3 % Н₂О, 5,5 % СН₄, 39,2 %N₂. Считая, что в печи достигнуто равновесие, установить, произошли ли изменения состава газа при охлаждении пробы до комнатной температуры и, если – да, то в каком направлении изменились содержания всех компонентов в пробе?

Решение. При отсутствии в газовой фазе измеримого содержания О₂ считаем, что равновесный состав смеси определяется реакциями (5)–(7), из которых только две являются независимыми. Выбираем реакции (5) и (6).

Для ответа на вопрос о равновесности газовой пробы применяем уравнение изотермы реакции:

Константу равновесия вычисляем из уравнения (см. пример 1.8). При 1000 К она равна .Тогда

Константу равновесия реакции (6)

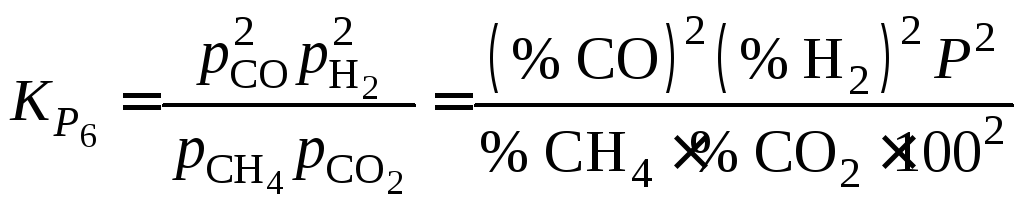
находим из выражения

,

где .

Определив при 1000 К , вычисляем:

Так как , то проба газа –неравновесная. При этом Значит, реакции (5) и (6) должны идти в прямом направлении при нагреве пробы газа сдо.

Равновесный газ должен отличаться от охлажденного (в пробе) меньшим %  и % и большим % СО и % . Содержание водорода (% ) по реакциям (5) и (6) изменяется противоположно. Но так как , то преимущественно должна протекать реакция (6). Поэтому в равновесном газе% > 14.

Преимущественное протекание реакции (6) приводит к увеличению общего числа моль газа. Поэтому при сохранении в газе постоянного абсолютного количества его относительное содержание в равновесном газе (% ) должно быть меньше, чем в пробе.

1.3.3. Роль углерода в формировании состава и свойств газовой фазы

Пример 1.11.Рассчитать состав газовой фазы СО – находящейся в равновесии с твердым углеродом, в интервале 700…1200 К для двух значений давления 1 и 10 атм. Вычислить равновесные давления кислорода в газовой смеси. Результаты расчета представить графически в координатах % СО –Ти–Т. На основе термодинамического анализа системы обозначить на графиках области устойчивости углерода и его оксидов, относящиеся к состояниям приР = 1 атм.

Решение. Для частной системы С – О при наличии твердого углерода число степеней свободы , то есть для количественного описания равновесного состояния достаточно значенийT и P в качестве независимых параметров. На первом этапе расчета пренебрегаем малой величиной .Определяющим является равновесие реакции газификации углерода (10). Связь переменных можно отразить системой уравнений:

.

Решение системы уравнений приводит к выражениям

Величину находим из выражения реакции (2).Значения иопределяем из выражения.

Необходимые для расчета величины вычисляем из справочных зависимостей:(Дж) и(Дж).Удобнее на основе указанных выражений получить температурные зависимости в виде и и использовать их для расчетов, результаты которых представлены в табл. 1.2 и графически (рис. 1.7 и 1.8).

Анализ полученных данных указывает на увеличение концентрации СО с увеличением температуры, что согласуется с эндотермическим характером реакции газификации (). Уменьшение % CO с ростом давления связано с увеличением объема (числа моль газов) системы () при превращении в СО по реакции (10). С ростом температуры и давления растет в системе в соответствии с происходящими изменениями в ее составе. Количественно это отражено кривыми линиями на рис. 1.7 и 1.8.

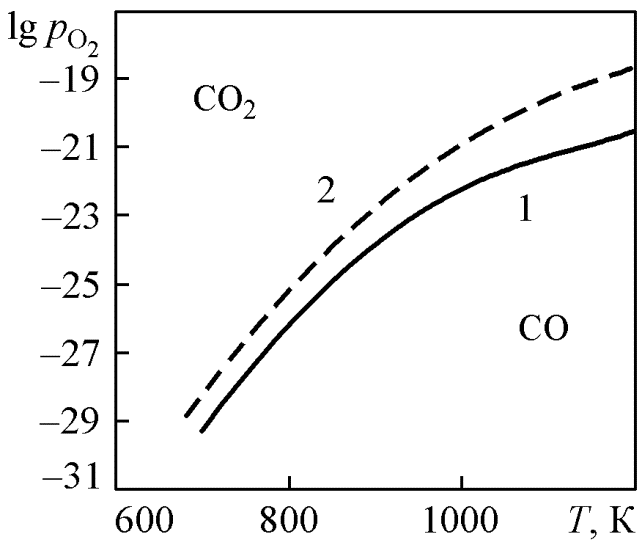
Рассмотрим состояние системы при Р = 1 атм.

Изобара 1 (см. рис. 1.7) разделяет диаграмму на две области различных состояний по отношению к равновесным. Запишем уравнение изотермы реакции (10)

,

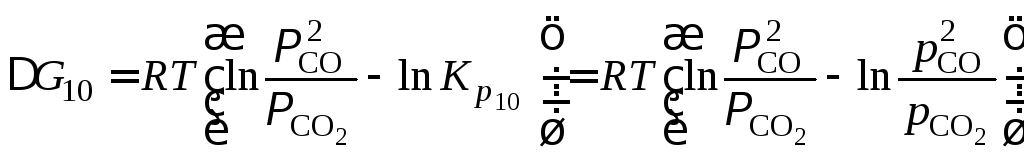где и– фактические, аи– равновесные давления газов.

В области выше равновесной кривой 1 при заданной Т фактический % СО больше равновесного % СО (точка кривой 1), значит, . Поэтому здесь ; реакция (10) должна идти в обратном направлении, в сто-

Таблица 1.2

Результаты расчета равновесного состава газа в системе С – О

Т, К			, атм				, атм
Р= 1 атм
700	2,65·10–4	1,1·1033	0,016		1,6	0,016	3,4·10–30	–29,5
800	0,011	5,8·1027	0,098		9,8	0,11	1,4·10–26	–25,8
900	0,19	4,6·1023	0,351		35,1	0,54	7,4·10–24	–23,1
1000	1,9	2,4·1020	0,724		72,4	2,62	6,0·10–22	–21,2
1100	12,5	5,0·1017	0,931		93,1	13,5	1,1·10–20	–19,9
1200	60,3	2,9·1015	0,984		98,4	61,5	9,1·10–20	–19,1
Р= 10 атм
700	2,65·10–4	1,1·1033	0,051		0,51	0,005	3,5·10–29	–28,5
800	0,011	5,8·1027	0,33		3,3	0,034	1,5·10–25	–24,8
900	0,19	4,6·1023	1,29		12,9	0,15	9,9·10–23	–22,0
1000	1,9	2,4·1020	35,1		35,1	0,54	1,4·10–20	–19,8
1100	12,5	5,0·1017	65,6		65,6	1,91	5,5·10–19	18,3
1200	60,3	2,9·1015	87,3		87,3	6,9	7,2·10–18	17,1
Рис. 1.7. Изобары равновесного состава газа СО – СО2 над твердым углеродом: 1 – 1 атм; 2 – 10 атм				Рис. 1.8. Температурная зависимость в системеCO – CO2 – Cтв: 1 – 1 атм; 2 – 10 атм

рону распада СО с образованием твердого углерода и . Таким образом, oбласть выше изобары – это область устойчивости углерода в контакте с , область распада СО. Обратные соотношения характерны для области ниже изобары. Это значит, что если поддерживать состав газовой фазы, удовлетворяющий соотношению, то углерод будет непрерывно расходоваться на взаимодействие с с образованием устойчивого оксида СО. Соответственно данному анализу на диаграммах обозначены области устойчивости оксидов углерода.

IIpимep 1.12. Определить состав равновесной газовой смеси, полученной при взаимодействии обогащенного кислородом воздуха с твердым углеродом, для заданных в таблице условий. Рассчитать равновесное давление кислородав смеси. Результаты представить графически в координатах % СО – Т;– Т и сравнить с результатами примера 1.11.

Состав обогащенного воздуха, об.%		Температура, К						Давление, атм
75	25	700	800	900	1000	1100	1200	1	10

Решение. Взаимодействие газовой смеси кислорода и азота с твердым углеродом при избытке последнего приводит к образованию смеси СО, , и ничтожно малого количества . Равновесная система является трехкомпонентной и двухфазной и по правилу фаз имеет число степеней свободы равное трем. Поэтому заданы 3 независимые переменные: Р, Т и. Расчет без определения представляет решение системы трех уравнений:

или

Здесь и.

Решение системы возможнона ЭВМ или из выражений:

Результаты расчета представлены в табл. 1.3 и графически (рис. 1.9 и 1.10). Относительное содержание СО и СО₂ в смеси находим из выражений:

и Сравнение полученных результатов с данными при тех же температурах и давлениях примера 1.11 показывают, что введение азота

в смесь СО –  приводит к увеличению равновесного отношения за счет увеличения СО и уменьшения в смеси. Иначе, равновесие реакции газификации (10) смещается вправо в сторону увеличения числа молей – эффект совпадает с влиянием давления при уменьшении последнего. Действительно, при разбавлении смеси азотом – газом, не участвующим в реакции, уменьшается сумма парциальных давлений реагентов СО и , что равноценно уменьшению давления в реакционной системе.

Таблица 1.3

Результаты расчета равновесного состава газа в системе С – О – N

T, К			Состав газовой смеси, об. %				атм		Относительное содержание в смеси, об. %
					N2
			Давление 1 атм
700	1,1·1033	2,6·10–4	0,81	24,49	74,70	0,03	8,5·10–31	–30,1	3,2	96,8
800	5,8·1027	0,011	4,86	21,96	73,18	0,22	3,5·10–27	–26,5	18,1	81,9
900	4,6·1023	0,19	16,68	14,57	68,74	1,14	1,7·10–24	–23,8	53,4	46,6
1000	2,4·1020	1,9	31,61	5,24	63,15	6,03	1,1·10–22	–21,9	85,8	14,2
1100	5,0·1017	12,5	38,14	1,16	60,70	32,80	1,9·10–21	–20,7	97,0	3,0
1200	2,9·1015	60,3	39,58	0,26	60,16	151,6	1,5·10–20	–19,8	99,3	0,7
			Давление 10 атм
700	1,1·1033	2,6·10–4	0,26	24,84	74,90	0,01	8,6·10–30	–29,1	1,0	99,0
800	5,8·1027	0,011	1,61	23,99	74,40	0,07	3,9·10–26	–25,4	6,3	93,7
900	4,6·1023	0,19	6,34	21,04	72,62	0,30	2,4·10–23	–22,6	23,2	76,8
1000	2,4·1020	1,9	16,67	14,58	68,75	1,14	3,2·10–21	–20,5	53,3	46,7
1100	5,0·1017	12,5	29,14	6,79	64,07	4,29	1,1·10–19	–19,0	81,1	18,9
1200	2,9·1015	60,3	36,46	2,21	61,33	16,46	1,2·10–18	–17,9	94,3	5,7

Пример 1.13.Составить систему уравнений связи между переменными для расчета при заданных значенияхР= 1 атм иТ = 2000 К равновесного состава газовой смеси, образующейся в реакторе с твердым углеродом при подаче в него воздуха с относительной влажностью 80 % при 20 °С. Состав сухого воздуха принять: 21 % и 79 % (по объему). Упругость пара воды при 293 К равна 17,7 мм рт. ст. Вычислить значения необходимых для расчета величин.

Рис. 1.9. Изобары равновесного состава газа СО – CO2 в присутствии азота над твердым углеродом: 1 – 1 атм; 2 – 10 атм	Рис. 1.10. Температурная зависимость системыCO–CO2 –N2–Cтв: 1– 1 атм; 2 – 10 атм

Решение. Исходный газ состоит из , и . При взаимодействии с  образуются , , .Cистема С – Н – О – N – четырехкомпонентная, двухфазная, четырехвариантная (). Для расчета равновесного состава газовой смеси необходимы четыре независимые переменные. ЭтоРиТ, а также два концентрационных параметраи .Тогда – неизвестные (вычисляемые) переменные. Парциальным давлениемпри 2000 К пренебрегаем. Система уравнений связи:

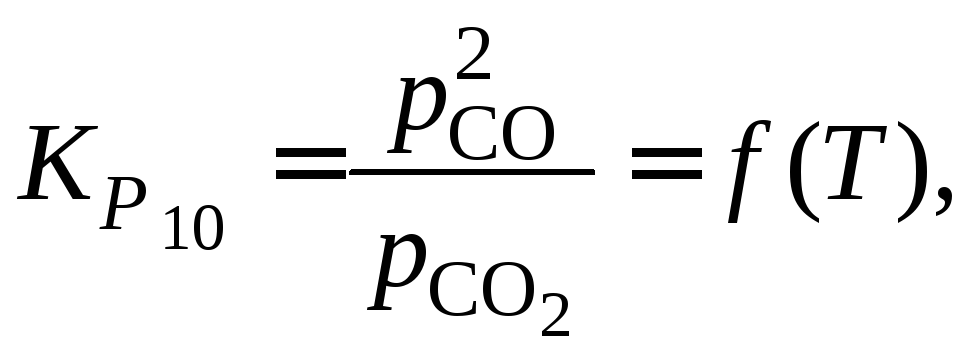
Константы равновесия реакций (10) и (5) находим из выражений:

и (см. примеры 1.8–1.11).

При 2000 К константы равны: и. Концентрационные параметры определяем из заданного состава воздуха. СодержаниеН₂О в воздухе соответствует мм рт. ст. и составляет«Штрих» относится к исходному составу воздуха. Содержание и в воздухе:

об. % %,

об. % %.

Тогда

Значения параметров ,, , иподставляем в систему уравнений и решаем ее (с помощью ЭВМ).