Р

Рис. 1.5. Схема сложного

Равновесия в системе с – н – о

ешение.В общем случае при горении метана образуется сложная газовая смесь, содержащая все реагенты реакций (1)–(12) и азот воздуха. При пиролизе метана или при распаде СО в системе может появиться твердый углерод. В этом случае устанавливается сложное равновесие (рис. 1.5) как сочетание частных равновесий.

В данной задаче будем считать, что по кинетическим причинам образование твердого углерода заторможено. Равновесия с участием С_тврассматривать не будем.

Данная система С – Н – О – Nявляется 4 компонентной () и однофазной (n = 1), значит, пятивариантной (). Для анализа необходимо знание пяти независимых параметров. ВыбираемР,Т,,,Тогданеизвестными оказываются равновесныедавления . Система уравнений связи:

Можно заметить, что возможна запись констант равновесия других 3 реакций. Однако следует проверить: действительно ли выбранные реакции независимы.

Исходное состояние смеси удобно записать в виде: . Тогда концентрационные параметры:

,и.

1.3.2. Упрощения расчетов равновесного состава газовой фазы

Часто содержания компонентов в газовых фазах металлургических систем – величины разного порядка. При температурах пирометаллургических процессов ивесьма малы. Тогда в системе С – Н – О расчет основан на реакциях (5) и (10). Эти реакции являются регулирующими состав в газовых атмосферах при использовании природного газа или увлажненного дутья в доменной печи, углеводородного топлива и других углеродсодержащих материалов в конвертере и других металлургических агрегатах и системах.

Р

Рис. 1.6. Равновесные отношения p_CO/p_CO2 и p_H2/p_H2O в газовой смеси CO – CO₂ – H₂ – H₂O при различных температурах

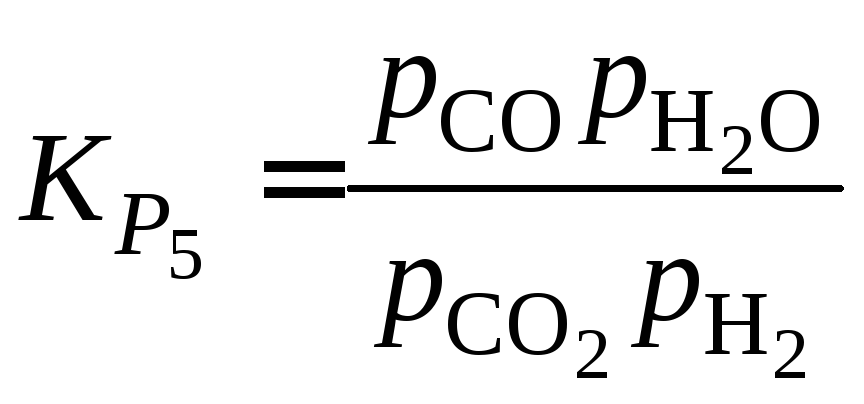еакция (5), называемая реакцией водяного газа, определяет соотношение между углеродсодержащими газами СО – СО₂и водородсодержащими Н₂ – Н₂О в равновесных сложных газовых смесях. При этом из выражения константы равновесияследует пропорциональность(при введении обозначенийи). Функциюможно представить графически (рис. 1.6). Для расчетаприменяют уравнение, полученное из выражения при подстановке в него зависимости(см. пример 1.4).

Следует отметить, что представленные простейшие изотермические зависимости дают строгую связь отношений и, но указывают и на неопределенность равновесных составов газовых смесей. Из графика при заданной температуре и значенииможно определить равновесное сx отношение и наоборот. Зная состав газовой атмосферы металлургического агрегата или системы, можно на основе графика решить вопрос о равновесности газовой фазы и спрогнозировать протекание процессов изменения ее состава и свойств. Если одно из отношений при определенной температуре на графике не соответствует другому, то смесь неравновесна. Ее следует рассматривать как исходную, и выполнить расчет равновесного состава сложного газа.

Все точки на изотермической прямой соответствуют состояниям системы с одним и тем же значением. Это означает, что различные по составу двухкомпонентные смеси характеризуются одинаковым сродством к кислороду и одинаковыми окислительно-восстановительными свойствами. При 1093 К, как было отмечено в примере 1.1, сродство к кислороду у водорода и СО одинаково, и это проявляется на графике равенством отношений (), так как при 1093 К. При всех других температурах равноценные по окислительно-восстановительным свойствам смеси имеют разные составы. Например, из графика следует, что смеси Н₂– Н₂О с отношением при 1400 К соответствует смесь СО – СО₂с отношением .

Пример 1.8. Привести методику расчета состава равновесной газовой фазы, образующейся из смеси СО₂и Н₂в отношении 3:1 при 1400 К. Определить равновесное давление кислорода.

Решение. Записываем уравнение реакции водяного газа (5) и вводим обозначения, характеризующие исходное и равновесное состояния газовой фазы:

исходный состав, моль 3 1 – –

равновесный состав, моль 3 – x 1 –x x x

. (1.12)

Отсюда получаем квадратное уравнение . Константу равновесия=2,417 при 1400 Квычисляем из выражения .Подставляя в уравнение(1.12), находим х = 0,858. Равновесный состав газа, мол. (об.) %:

.

Равновесное давление кислорода находим из выражений для константы равновесия и реакции (1):

,

где константа равновесия при 1400 К.

Тогда

атм.

Вычисленное значение подтверждает весьма низкие содержания молекулярного кислорода в высокотемпературной газовой фазе системы .

Пример 1.9.Рассчитать состав равновесной газовой фазы, образующейся из смеси природного газа и воздуха, подаваемой в нагревательную печь в соотношении 1:5. Температура печи поддерживается постоянной и равной 1600 К. ДавлениеР=1 атм. Вычислить равновесные давления кислорода и метана в газовой смеси.

Исходный состав природного газа: 83 об. % СН₄; 16 об. % С₂Н₆; 1 об. % N₂. Состав воздуха: 21 об. % О₂; 79 об. % N₂.

Решение. Считаем, что содержания СН₄, С₂Н₆и О₂в равновесной смеси ничтожно малы. АзотN₂не реагирует, и его количество в равновесной и исходной смесях одно и то же.

Тогда равновесие определяется реакцией водяного газа (5). При указанных упрощениях необходимо вычислить 4 неизвестные величины, определяющие содержание компонентов, указанных в уравнении(5).

Выражаем константу равновесия через количество молей реагентов

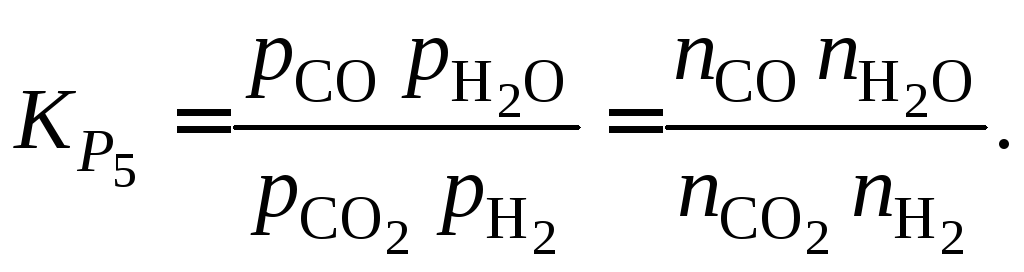
Записываем еще три необходимые уравнения на основе материального баланса по каждому элементу в газовой фазе:

«Штрих» относится к исходному составу газовой смеси.

В расчете на 1 моль природного газа исходная смесь содержит:

моль;моль;моль;3,96 моль.

Тогда

(1.13)

(1.14)

.(1.15)

Из выражения (см. пример 1.8) дляК

(1.16)

Решение системы 4 уравнений (1.13–1.16) возможно на ЭВМ. Можно также после преобразований получить и решить квадратное уравнение:

,

из которого моль. Количества остальных реагентов из уравнений (1.13–1.16):;;моль. С учетоммоль мольные доли газов равновесной смеси равны:

и соответствуют мольному (объемному) составу (%) смеси: