ТИК-контр-з / Спектры периодических сигналов

Спектры периодических сигналов

Если функция u(t) задана в интервале и удовлетворяет условиям Дирихле (непрерывная, имеет конечное число точек разрыва 1-ого рода и конечное число экстремальных точек), повторяется с периодом на протяжении времени от до и если в качестве базисных функций выбраны экспоненциальные функции, то ее можно записать в виде:

, (1)

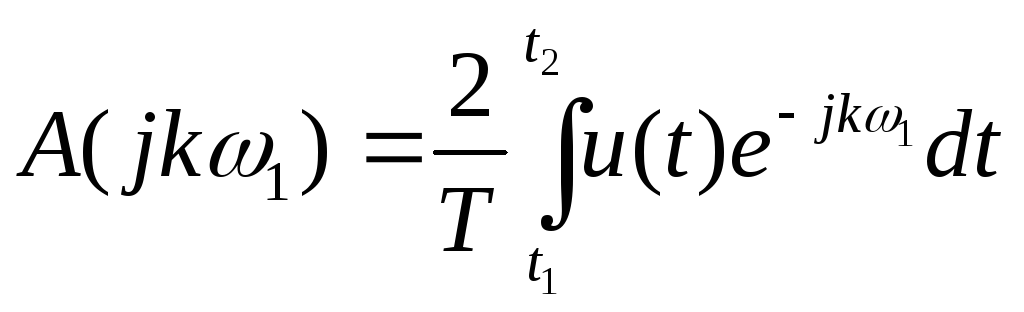. (2)

Выражение (1) – ряд Фурье в комплексной форме, а (2) – комплексный спектр периодического сигнала u(t), спектр дискретный.

Огибающая комплексного спектра имеет вид:

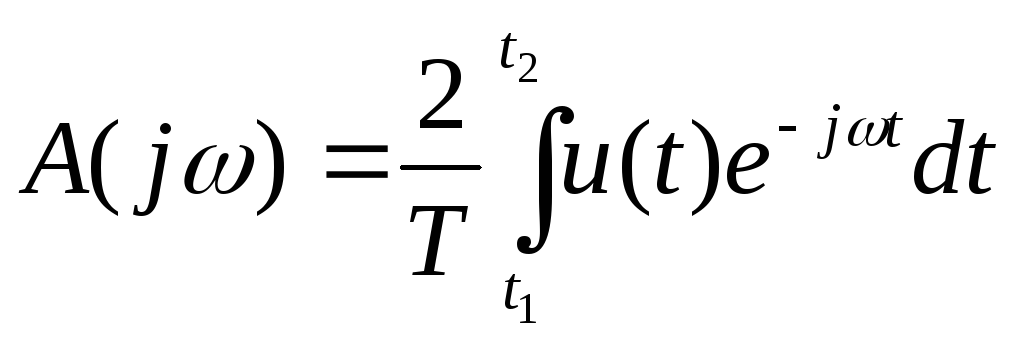. (3)

Комплексный спектр можно представить в виде:

, (4)

где - спектр амплитуд, - спектр фаз.

Пользуясь формулой Эйлера:

,

можно представить в виде действительной и мнимой частей:

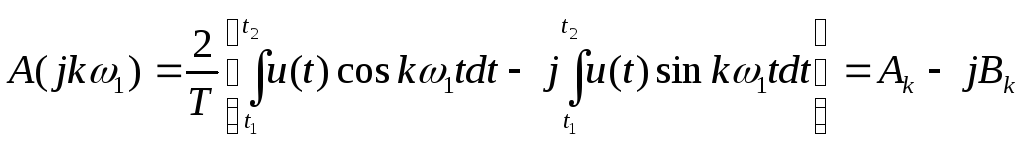. (5)

Спектр амплитуд - четная функция, спектр фаз - функция нечетная.

При получаем постоянную составляющую:

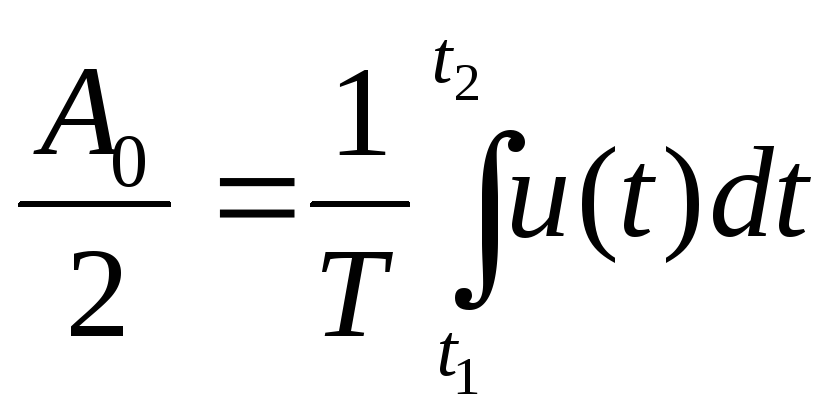. (6)

Можно перейти от двустороннего спектрального представления к одностороннему (без отрицательных частот), объединяя комплексные сопряженные корни. Тогда получим ряд Фурье в тригонометрической форме:

, (7)

или в виде

(8)

Огибающую спектра амплитуд можно получить, заменив в на , де для -й гармоники.

Пример 1.

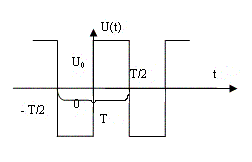
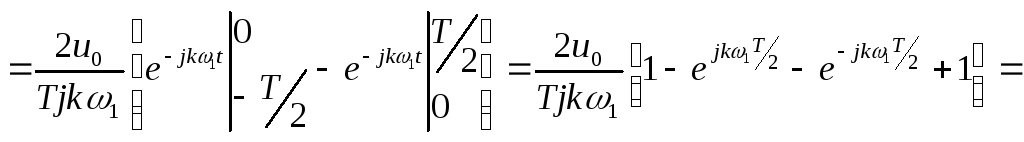
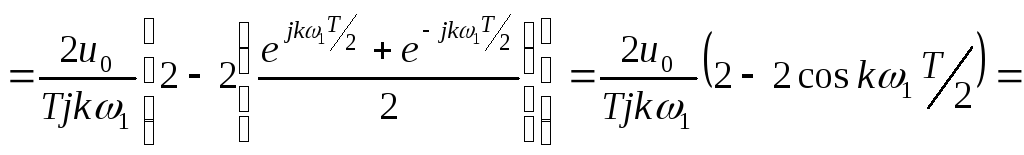
Так как , то

.

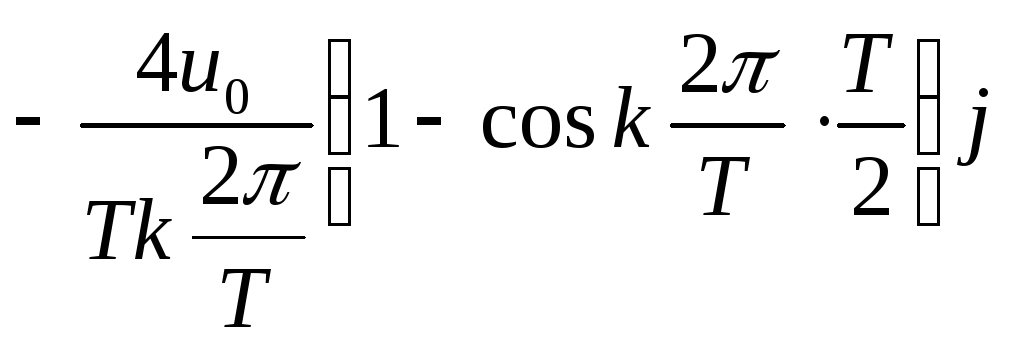
Отметим, что

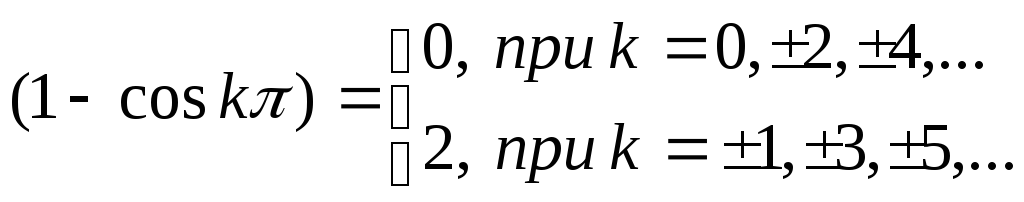
Тогда

Амплитуда гармоник ;

;

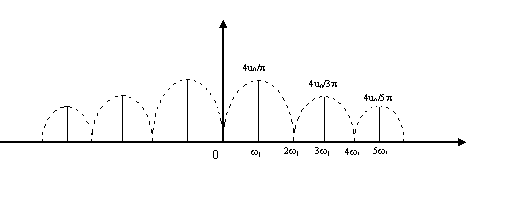
Восстановим периодическую последовательность , вычислив несколько первых членов ряда Фурье и проследив, как сумма сходится к указанному сигналу.

Функция является нечетной, поэтому

;

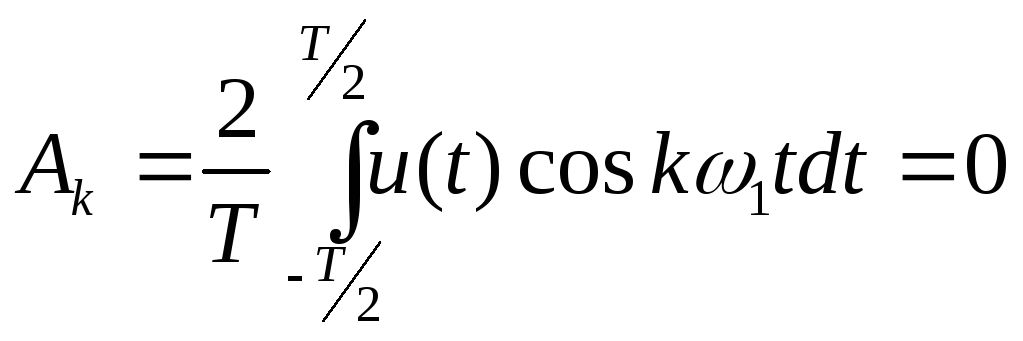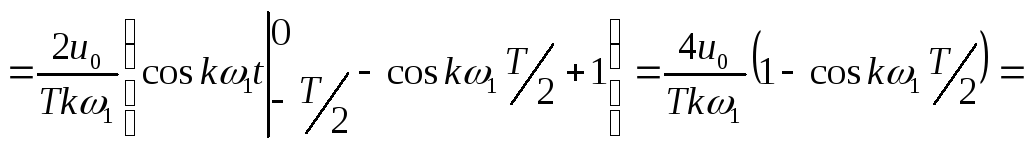
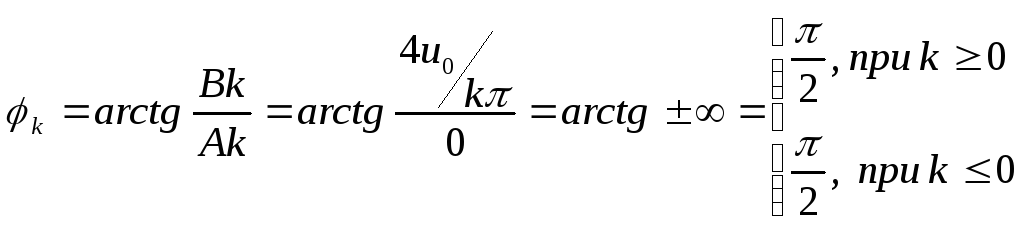
Спектры непериодических сигналов

Любой физически реализуемый сигнал ограничен во времени и обладает конечной энергией. Модели таких сигналов также могут быть представлены совокупностью гармонических составляющих в виде:

, (1)

где - базисная функция, - спектральная плотность.

С увеличением периода Т значения амплитуд спектральных составляющих уменьшаются. Так как частоты составляющих спектра кратны основной частоте, то при ее уменьшении линии на спектральной диаграмме сближаются.

Спектральное представление для одиночного импульса можно получить увеличение периода сигнала до бесконечности.

Пару преобразований Фурье для периодической функции запишем в форме:

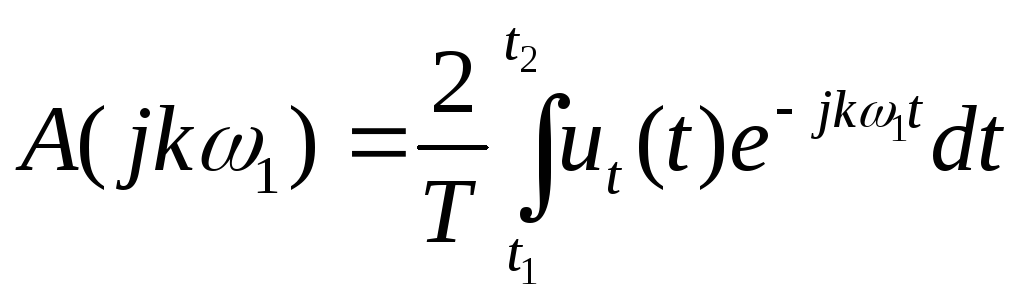
При , переходит в , частота уменьшается до , а превращается в текущую частоту.

Заменяя суммирование интегрированием, находим:

Обозначив интеграл в квадратных скобках через , получим спектральную плотность (спектральная характеристика), получим формулы прямого и обратного интегрального преобразования Фурье:

,

.

На каждой конкретной частоте амплитуда соответствующей составляющей равна нулю. Бесконечно малому интервалу частоты составляющая с бесконечно малой комплексной амплитудой .

. (4)

Огибающая спектра периодической функции имеет вид:

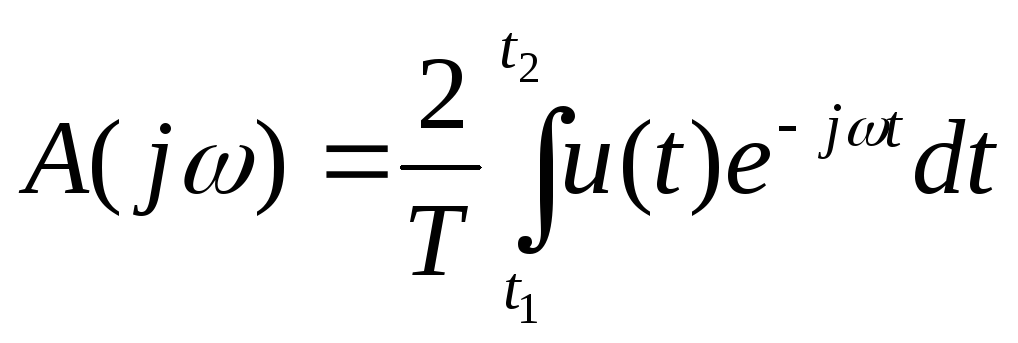
Сравнивая ее с (2), видим, что они различаются только множителем

. (5)

Поэтому по известной спектральной характеристике одиночного импульса легко построить линейчатый спектр их периодической последовательности.

Так как - величина комплексная, она может быть записана в виде:

, (6)

где - спектральная плотность амплитуд – спектр непериодического сигнала, спектральная плотность фаз.

Так как составляющие расположены на всех частотах, то спектр непериодического сигнала является непрерывным или сплошным.

Спектральную характеристику можно представить состоящую из действительной и мнимой частей:

(7)

где

(8)

(9)

Модуль и фаза спектральной характеристики определяется выражениями:

- функция четная; (10)

- функция нечетная; (11)

Комплексная форма интегрального преобразования Фурье легко приводится к тригонометрической:

;

тогда

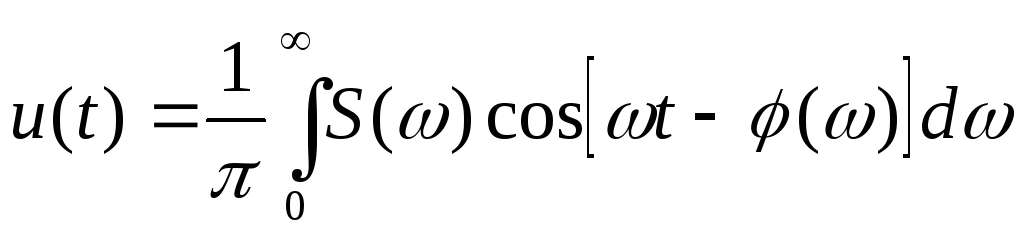(12)

Пример:

Определить спектр дельта-функции.

Запишем выражение для спектральной характеристики дельта-функции:

С учетом того, что с помощью дельта-функции можно выразить значение реального сигнала в конкретный момент времени в виде:

,

будем иметь

,

откуда модуль спектральной характеристики

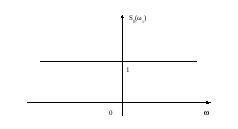
Следовательно, дельта-функции соответствует сплошной равномерный спектр, включающий в себя составляющие бесконечно больших частот. При фазы всех составляющих равны нулю.

Пример.

Определить спектр экспоненциального импульса.

;

;

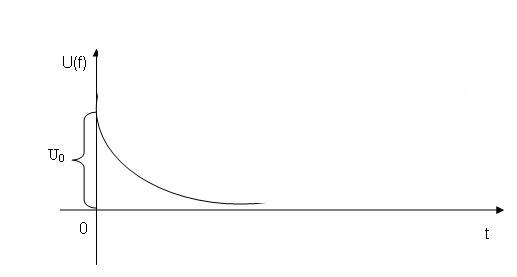
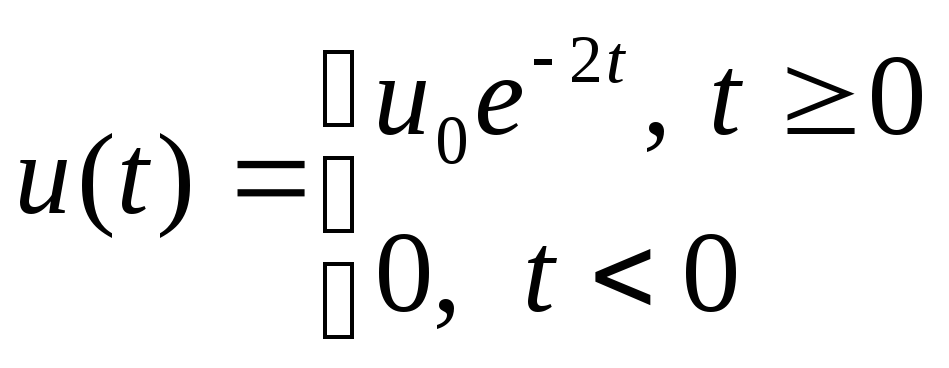
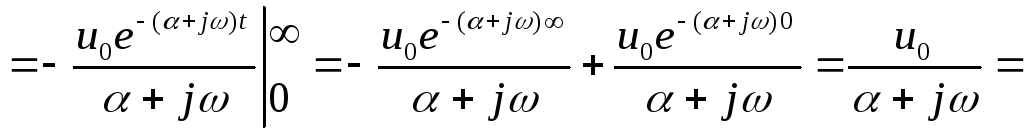
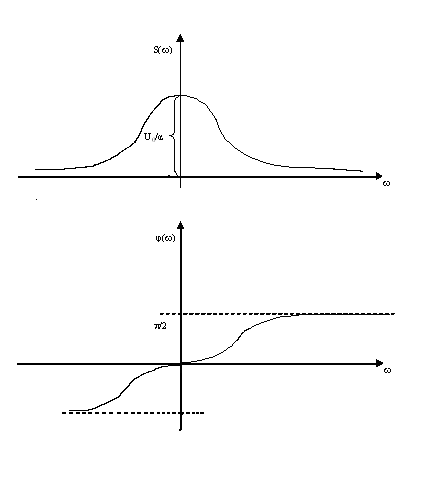
Следствие.

Спектр функции Хевисайда, для которой 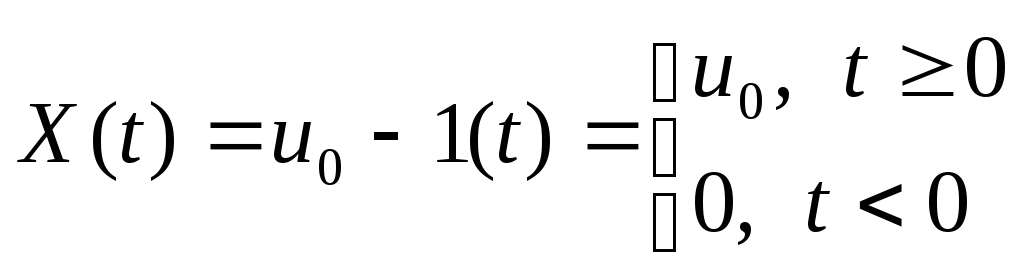, неприменимо условие абсолютной интегрируемости и, следовательно, к ней нельзя применить преобразование Фурье. Вместе с тем ее можно считать экспоненциальной функцией. Тогда

Пример.

.
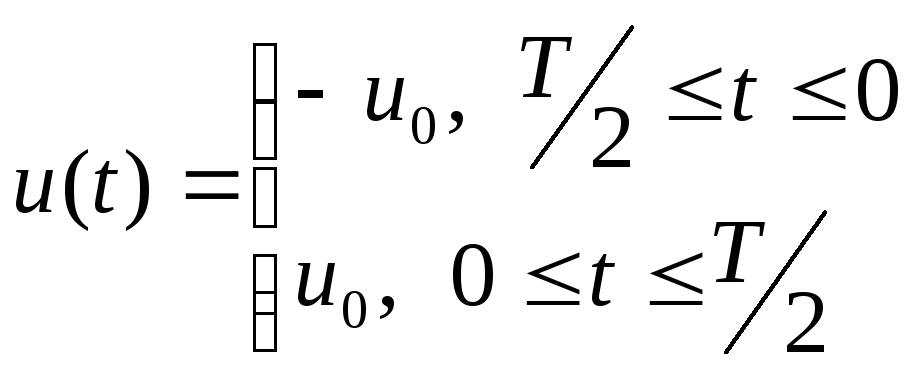
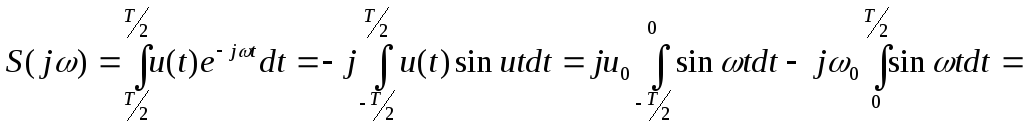
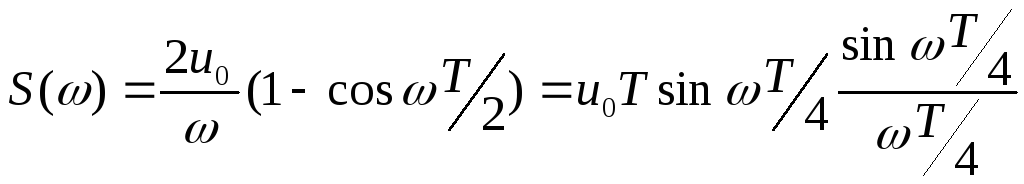