23

Министерство образования РФ

Московский государственный институт электроники и математики (Технический университет)

КАФЕДРА "ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА"

Методические указания

по выполнению лабораторной работы №1

"Преобразования на плоскости. Вычерчивание линий и окружностей"

по курсу

"Компьютерная графика"

Москва, 1999 г.

1. Цель работы

Известно, что объекты, которые отображаются на дисплее компьютера, могут быть преобразованы или трансформированы по какому-либо закону для достижения некоторого эффекта. Кроме того, эти графические объекты должны быть представлены в растровом формате, т.к. дисплей является растровым графическим устройством.

Поэтому целью данной работы является изучение алгоритмов:

1. преобразования объектов на плоскости;

2. разложения графической информации в растр.

2. Теоретическая часть

2. 1. Преобразования на плоскости (2d преобразования)

Преобразование - это изменение координат некоторой точки М на плоскости по некоторому закону : M(x,y) -> M’(x,y).

Существуют следующие элементарные преобразования на плоскости:

–поворот вокруг начальной точки на угол ;

• масштабирование;

• зеркальное отражение;

• параллельный перенос.

Все эти виды преобразований могут быть представлены

• общим аффинным преобразованием.

1. Поворот описывается формулами

3. 2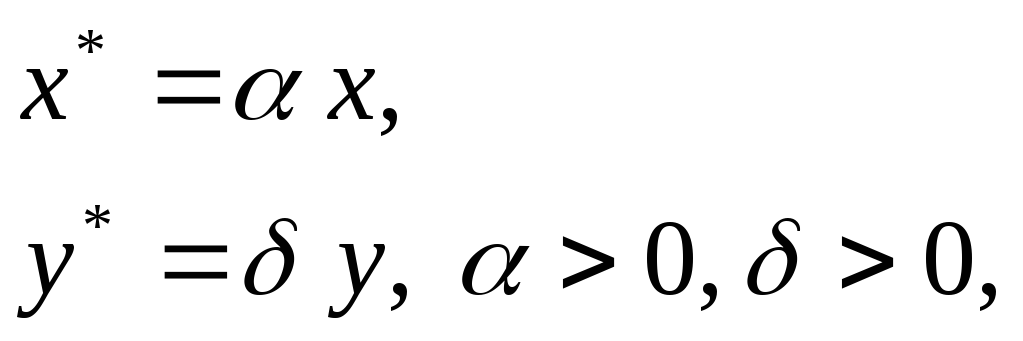.Масштабирование можно задать так:

где коэффициенты масштабирования.

Виды масштабирования

растяжение вдоль оси х	сжатие вдоль оси х	Растяжение вдоль оси у	сжатие вдоль оси у

3. Зеркальное отражение задается формулами:

Относительно оси абсцисс	Относительно оси ординат

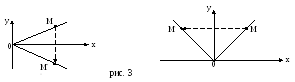
4. Параллельный перенос можно описать формулами:

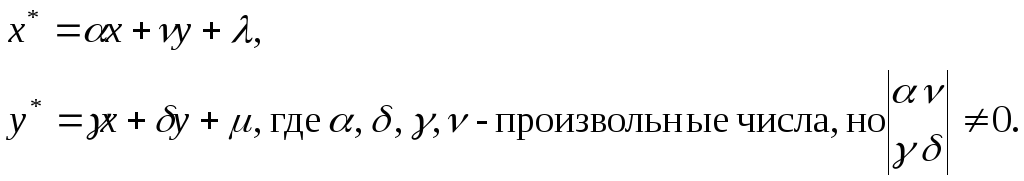4. 5. Общее аффинное преобразование описывается следующими соотношениями

Любое аффинное преобразование может быть представлено как последовательное выполнение (суперпозиция) простейших преобразований, описанных в предыдущих четырех пунктах.

Примеры аффинного преобразования:

1. Поворот фигуры относительно точки С, не являющейся началом координат, на заданный угол осуществляется за 3 шага (см. рис. 5, а):

• параллельный перенос фигуры так, чтобы данная точка С оказалась в точке начале координат (см. рис.5, б);

• поворот фигуры относительно начала координат на заданный угол (см. рис. 5, в);

• параллельный перенос фигуры на исходное место (см. рис. 5, г).

а) б) в) г)

Рис. 5

2. Зеркальное отражение фигуры относительно прямой, не параллельной ни одной из осей координат осуществляется также за 3 шага (см. рис. 6, а):

• зная тангенс угла наклона прямой, повернуть на этот угол фигуру (см. рис. 6, б);

• зеркально отразить фигуру относительно оси х (см. рис. 6, в);

• повернуть отраженную фигуру на известный угол, взятый с противоположным знаком (см. рис. 6, г).

а) б) в) г)

Рис. 6