
- •Содержание
- •1. Исходные данные
- •2. Расчет схемы замещения
- •3.Анализ статической устойчивости установившехся режимов простейшей электрической системы
- •3.2Анализ устойчивости установившегося режима
- •3.3 Расчет угловой характеристики для синхронного генератора, имеющего регулятор тока возбуждения пропорционального вида.
- •4.Анализ устойчивости динамических переходов
- •4.1 Анализ устойчивости динамических переходов без учета демпфирования
- •4.2 Анализ динамической устойчивости с учетом демпфирования.
- •5.Анализ устойчивости простого динамического перехода
- •5.1 Анализ устойчивости динамических переходов без учета демпфирования
- •5.2 Анализ динамической устойчивости с учетом демпфирования.
- •Библиографический список
5.Анализ устойчивости простого динамического перехода
5.1 Анализ устойчивости динамических переходов без учета демпфирования
Последовательный анализ режимов работы энергосистемы.
Нормальный режим



Аварийный режим. Двухфазное короткое замыкание в начале ЛЭП длительностью




Послеаварийный режим. Отключение поврежденной ЛЭП


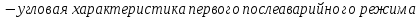



Характеристика после аварийного режима переходит только на после аварийный режим, тогда можно определить предельно допустимый угол отключения:



Численное интегрирование уравнения движения ротора с использованием метода последовательных интервалов
Для метода последовательно интегрирования используются следующие данные и формулы:
Примем ∆t
= 0,02c,
δ0
=
 ,
τj
= 4,88 с
,
τj
= 4,88 с






Результаты интегрирования сведены в таблицу 5.
Таблица 5 – Данные интегрирования
|
интервал |
t,с |
∆P,МВт |
∆δ,град |
δ,град |
∆W,1/с |
W,1/с |
|
0 |
0 |
0 |
0 |
23.05 |
0 |
314 |
|
1 |
0.02 |
1561.750 |
0.958 |
24.008 |
0.836 |
314.836 |
|
2 |
0.04 |
1528.929 |
1.896 |
25.904 |
1.654 |
316.489 |
|
3 |
0.06 |
1464.704 |
2.794 |
28.698 |
2.437 |
318.926 |
|
4 |
0.08 |
1371.926 |
3.636 |
32.334 |
3.171 |
322.097 |
|
5 |
0.1 |
1254.895 |
4.405 |
36.739 |
3.842 |
325.940 |
|
6 |
0.12 |
1119.301 |
5.092 |
41.831 |
4.441 |
330.381 |
|
7 |
0.14 |
972.043 |
5.688 |
47.519 |
4.961 |
335.342 |
|
8 |
0.16 |
820.907 |
6.192 |
53.711 |
5.401 |
340.743 |
|
9 |
0.18 |
674.096 |
6.605 |
60.316 |
5.761 |
346.504 |
|
10 |
0.2 |
539.695 |
6.936 |
67.252 |
6.050 |
352.554 |
|
11 |
0.22 |
425.142 |
7.197 |
74.449 |
6.277 |
358.831 |
|
12 |
0.24 |
336.827 |
7.404 |
81.853 |
6.458 |
365.289 |
|
13 |
0.26 |
279.876 |
7.575 |
89.428 |
6.607 |
371.896 |
|
14 |
0.28 |
258.161 |
7.734 |
97.161 |
6.745 |
378.642 |
|
15 |
0.3 |
274.517 |
7.902 |
105.063 |
6.892 |
385.534 |
|
16 |
0.32 |
331.121 |
8.105 |
113.169 |
7.069 |
392.603 |
|
17 |
0.34 |
429.939 |
8.369 |
121.537 |
7.299 |
399.903 |
|
18 |
0.36 |
573.202 |
8.720 |
130.258 |
7.606 |
407.509 |
|
19 |
0.38 |
763.776 |
9.189 |
139.447 |
8.015 |
415.524 |
Как видно из таблицы 5, в момент времени t = 0,34 с угол δ превышает δmaxоткл. Тогда, для простого динамического перехода примем время tпроткл равное 0,32 с, полученные результаты сведены в таблицу 6 и представлены на рисунках 19-21
Таблица 6 – Данные интегрирования простого динамического
перехода без учета демпфирования
|
интервал |
t,с |
∆P,МВт |
∆δ,град |
δ,град |
∆W,1/с |
W,1/с |
|
0 |
0 |
0 |
0 |
23.05 |
0 |
314 |
|
1 |
0.02 |
1561.750 |
0.958 |
24.008 |
0.836 |
314.836 |
|
2 |
0.04 |
1528.929 |
1.896 |
25.904 |
1.654 |
316.489 |
|
3 |
0.06 |
1464.704 |
2.794 |
28.698 |
2.437 |
318.926 |
|
4 |
0.08 |
1371.926 |
3.636 |
32.334 |
3.171 |
322.097 |
|
5 |
0.1 |
1254.895 |
4.405 |
36.739 |
3.842 |
325.940 |
|
6 |
0.12 |
1119.301 |
5.092 |
41.831 |
4.441 |
330.381 |
|
7 |
0.14 |
972.043 |
5.688 |
47.519 |
4.961 |
335.342 |
|
8 |
0.16 |
820.907 |
6.192 |
53.711 |
5.401 |
340.743 |
|
9 |
0.18 |
674.096 |
6.605 |
60.316 |
5.761 |
346.504 |
|
10 |
0.2 |
539.695 |
6.936 |
67.252 |
6.050 |
352.554 |
|
11 |
0.22 |
425.142 |
7.197 |
74.449 |
6.277 |
358.831 |
|
12 |
0.24 |
336.827 |
7.404 |
81.853 |
6.458 |
365.289 |
|
13 |
0.26 |
279.876 |
7.575 |
89.428 |
6.607 |
371.896 |
|
14 |
0.28 |
258.161 |
7.734 |
97.161 |
6.745 |
378.642 |
|
15 |
0.3 |
274.517 |
7.902 |
105.063 |
6.892 |
385.534 |
|
16 |
0.32 |
-1360.106 |
7.068 |
112.131 |
6.165 |
391.699 |
|
17 |
0.34 |
-2830.190 |
5.332 |
117.463 |
4.650 |
396.349 |
|
18 |
0.36 |
-2610.592 |
3.730 |
121.193 |
3.254 |
399.603 |
|
19 |
0.38 |
-2431.062 |
2.239 |
123.433 |
1.953 |
401.556 |
|
20 |
0.4 |
-2313.419 |
0.820 |
124.253 |
0.716 |
402.272 |
|
21 |
0.42 |
-2268.513 |
-0.571 |
123.682 |
-0.498 |
401.773 |
|
22 |
0.44 |
-2299.879 |
-1.982 |
121.700 |
-1.729 |
400.045 |
Продолжение таблицы 6
|
23 |
0.46 |
-2405.081 |
-3.457 |
118.243 |
-3.015 |
397.030 |
|
24 |
0.48 |
-2574.777 |
-5.036 |
113.207 |
-4.393 |
392.637 |
|
25 |
0.5 |
-2789.475 |
-6.747 |
106.459 |
-5.885 |
386.752 |
|
26 |
0.52 |
-3014.125 |
-8.596 |
97.863 |
-7.498 |
379.254 |
|
27 |
0.54 |
-3191.503 |
-10.554 |
87.310 |
-9.205 |
370.049 |
|
28 |
0.56 |
-3237.477 |
-12.540 |
74.770 |
-10.937 |
359.111 |
|
29 |
0.58 |
-3044.706 |
-14.407 |
60.363 |
-12.566 |
346.545 |
|
30 |
0.6 |
-2504.055 |
-15.943 |
44.420 |
-13.906 |
332.639 |
|
31 |
0.62 |
-1548.659 |
-16.893 |
27.527 |
-14.734 |
317.905 |
|
32 |
0.64 |
-207.218 |
-17.020 |
10.507 |
-14.845 |
303.060 |
|
33 |
0.66 |
1371.302 |
-16.179 |
-5.672 |
-14.112 |
288.948 |
|
34 |
0.68 |
2957.496 |
-14.365 |
-20.037 |
-12.529 |
276.419 |
|
35 |
0.7 |
4332.770 |
-11.707 |
-31.744 |
-10.211 |
266.208 |
|
36 |
0.72 |
5368.027 |
-8.415 |
-40.158 |
-7.339 |
258.868 |
|
37 |
0.74 |
6038.231 |
-4.711 |
-44.869 |
-4.109 |
254.759 |
|
38 |
0.76 |
6380.132 |
-0.797 |
-45.667 |
-0.696 |
254.064 |
|
39 |
0.78 |
6435.412 |
3.150 |
-42.517 |
2.747 |
256.811 |
|
40 |
0.8 |
6212.619 |
6.961 |
-35.556 |
6.071 |
262.882 |
|
41 |
0.82 |
5680.495 |
10.445 |
-25.111 |
9.110 |
271.993 |
|
42 |
0.84 |
4794.023 |
13.385 |
-11.726 |
11.675 |
283.668 |
|
43 |
0.86 |
3546.452 |
15.561 |
3.835 |
13.572 |
297.240 |
|
44 |
0.88 |
2022.746 |
16.801 |
20.636 |
14.655 |
311.894 |
|
45 |
0.9 |
411.887 |
17.054 |
37.690 |
14.875 |
326.769 |
|
46 |
0.92 |
-1049.130 |
16.410 |
54.100 |
14.314 |
341.083 |
|
47 |
0.94 |
-2170.241 |
15.079 |
69.180 |
13.153 |
354.235 |
|
48 |
0.96 |
-2874.131 |
13.316 |
82.496 |
11.615 |
365.850 |
|
49 |
0.98 |
-3195.032 |
11.357 |
93.853 |
9.906 |
375.756 |
|
50 |
1 |
-3231.462 |
9.375 |
103.227 |
8.177 |
383.933 |
Угловая характеристика простого динамического перехода представлена на рисунке 18.

Рисунок 18 – Угловая характеристика простого динамического перехода

Рисунок 19 – Зависимость угла от времени ПП

Рисунок 20 – Зависимость скорости от времени

Рисунок 21 – Зависимость изменения скорости от времени ПП
Расчет площадок торможения и ускорения:
Площадка ускорения находится в интервале от δ0 = 23,050до δ1 = 112,130 и ограничена характеристиками Р0 и РАР.

Площадка торможения находится в интервале от δ1 = 112,130 до δ2 = 154,80 и ограниченная характеристиками Р0 и РПАР1.

 следовательно,
динамический переход устойчив.
следовательно,
динамический переход устойчив.
Площадки торможения и ускорения представлены на рисунке 21
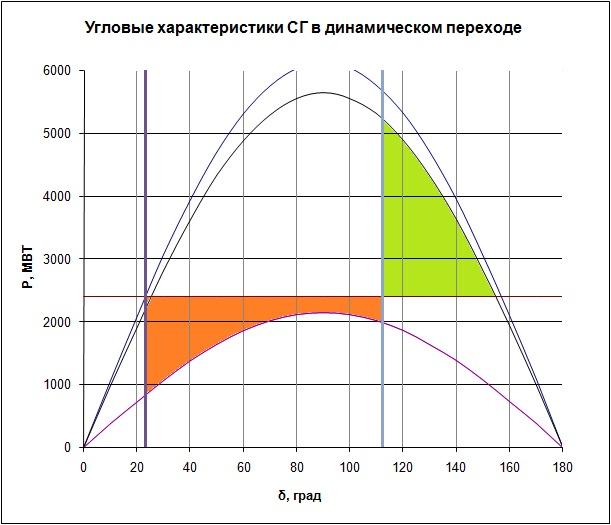
Рисунок 22 – площадки ускорения и торможения
