3.3 Расчет угловой характеристики для синхронного генератора, имеющего регулятор тока возбуждения пропорционального вида.

При наличии у синхронного генератора АРВ ПД его угловая характеристика зависит от двух переменных: угла δ и поперечной синхронной ЭДС Eq.

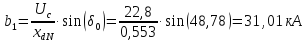
T_e – постоянная времени возбуждения возбудителя принимается равной 0,2 с.

Результаты расчета ЭДС СГ и его угловая характеристика представлены на рисунках 8 и 9 соответственно.

Рисунок8 – Зависимость ЭДС от угла

Рисунок9 – Угловая характеристика СМ

Согласно рисунку 9, можно найти значения максимальной мощности СГ и соответствующий ему угол:

P_Eq^max=9787,77 МВт, δ_пред=112,4⁰

4.Анализ устойчивости динамических переходов

4.1 Анализ устойчивости динамических переходов без учета демпфирования

Последовательный анализ режимов работы энергосистемы.

1. Нормальный режим

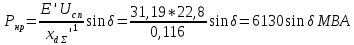
2. Аварийный режим. Двухфазное короткое замыкание в начале ЛЭП длительностью t=0.34 с

Сопротивление обратной последовательности:

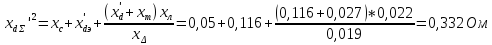
3. Первый послеаварийный режим. Отключение поврежденной ЛЭП t = 0.16c

4. Второй послеаварийный режим. Неуспешное АПВ поврежденной цепи после которого линия включается на КЗ t=0.15

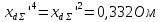
Динамический переход представлени на рисунке 10.

Рисунок10 – Угловые характеристики

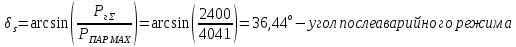
Предположим, что характеристика после аварийного режима переходит только на после аварийный режим, тогда можно определить предельно допустимый угол отключения:

Численное интегрирование уравнения движения ротора с использованием метода последовательных интервалов

Для метода последовательно интегрирования используются следующие данные и формулы:

Примем ∆t = 0,02c, δ₀ = , τj = 4,88 с

Результаты интегрирования сведены в таблицу 4 и представлены на рисунках 11-13.

Рисунок11 – Зависимость угла от времени ПП

Таблица 3 – Данные интегрирования

интервал	t,с	∆P,МВт	∆δ,град	δ,град	∆W,1/с	W,1/с
0	0	0	0	23.05	0	314
1	0.02	1561.750	0.958	24.008	0.836	314.836
2	0.04	1528.929	1.896	25.904	1.654	316.489
3	0.06	1464.704	2.794	28.698	2.437	318.926
4	0.08	1371.926	3.636	32.334	3.171	322.097
5	0.1	1254.895	4.405	36.739	3.842	325.940
6	0.12	1119.301	5.092	41.831	4.441	330.381
7	0.14	972.043	5.688	47.519	4.961	335.342
8	0.16	820.907	6.192	53.711	5.401	340.743
9	0.18	674.096	6.605	60.316	5.761	346.504
10	0.2	539.695	6.936	67.252	6.050	352.554
11	0.22	425.142	7.197	74.449	6.277	358.831
12	0.24	336.827	7.404	81.853	6.458	365.289
13	0.26	279.876	7.575	89.428	6.607	371.896
14	0.28	258.161	7.734	97.161	6.745	378.642
15	0.3	274.517	7.902	105.063	6.892	385.534
16	0.32	331.121	8.105	113.169	7.069	392.603
17	0.34	-1180.507	7.381	120.550	6.438	399.041
18	0.36	-2463.532	5.870	126.419	5.120	404.161
19	0.38	-2145.352	4.554	130.973	3.972	408.133
20	0.4	-1865.510	3.410	134.383	2.974	411.107
21	0.42	-1638.265	2.405	136.788	2.098	413.205
22	0.44	-1469.351	1.504	138.292	1.311	414.516
23	0.46	-1360.261	0.669	138.961	0.584	415.100
24	0.48	-1310.868	-0.135	138.826	-0.118	414.983
25	0.5	-166.495	-0.237	138.589	-0.207	414.776
26	0.52	981.223	0.365	138.954	0.318	415.094
27	0.54	991.468	0.973	139.927	0.849	415.943
28	0.56	1019.062	1.598	141.525	1.394	417.337
29	0.58	1065.241	2.252	143.777	1.964	419.301
30	0.6	1132.052	2.946	146.723	2.569	421.870

Продолжение таблицы 3

31	0.62	1222.404	3.696	150.419	3.223	425.094
32	0.64	1340.120	4.518	154.936	3.940	429.034
33	0.66	1489.950	5.432	160.368	4.738	433.772
34	0.68	1677.483	6.461	166.828	5.635	439.407
35	0.7	1908.838	7.631	174.460	6.656	446.063
36	0.72	2189.915	8.975	183.434	7.828	453.891
37	0.74	2524.846	10.523	193.958	9.179	463.069
38	0.76	2913.085	12.310	206.268	10.737	473.807
39	0.78	3344.456	14.362	220.629	12.526	486.333
40	0.8	3791.591	16.687	237.317	14.555	500.888
41	0.82	4200.386	19.264	256.580	16.802	517.690
42	0.84	4482.344	22.013	278.593	19.200	536.890
43	0.86	4518.702	24.785	303.378	21.618	558.508
44	0.88	4191.830	27.356	330.733	23.860	582.368
45	0.9	3452.611	29.474	360.207	25.707	608.076
46	0.92	2399.087	30.945	391.152	26.991	635.067
47	0.94	1298.288	31.741	422.894	27.686	662.752
48	0.96	496.972	32.046	454.940	27.951	690.704
49	0.98	265.267	32.209	487.149	28.093	718.797
50	1	687.144	32.630	519.779	28.461	747.258

Рисунок12 – Зависимость скорости от времени

Рисунок 13 – Зависимость изменения скорости от угла

Расчет площадок торможения и ускорения:

Площадка ускорения находится в интервале от δ₀ = 23,05⁰до δ₁ = 120,6⁰ и ограничена характеристиками Р₀ и Р_АР.

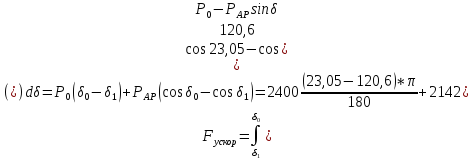
Площадка торможения находится в интервале от δ₁ = 120,6⁰ до δ₂ = 138,6⁰ и ограниченная характеристиками Р₀ и Р_ПАР1.

Площадка ускорения в ПАР находится в интервале от δ₂ = 138,6⁰до δ₃ = 160,4⁰ и ограничена характеристиками Р₀ и Р_АР.

следовательно, динамический переход неустойчив.

Площадки торможения и ускорения представлены на рисунке 14.

Рисунок 14 – площадки ускорения и торможения