2. Расчет схемы замещения

На схеме замещения (рис. 3) в зависимости от условий работы ЭДС и сопротивления эквивалентного СГ имеют переменные значения.

Рисунок 3 – Эквивалентная схема замещения электрической системы

Элементы схемы замещения приводим к номинальному напряжению генератора, а так же учитываем количество единиц оборудования.

1.Генератор ТВВ – 800

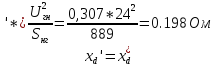
2.Трансформатор ОРЦ – 330000/525

3.ЛЭП

3.Анализ статической устойчивости установившехся режимов простейшей электрической системы

3.1 Угловые характеристики для трех моделей : без АРВ, с АРВ ПД, с АРВ СД. Значение ЭДС синхронного генератора для различных режимов:

Значение угла режима:

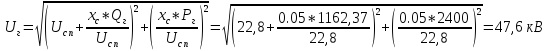
Численные значения угловых характеристик имеют вид:

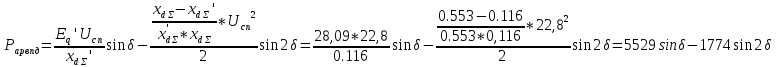
Результаты расчета угловых характеристик по приведенным выше зависимостям представлены на рис. 4.

Рисунок 4 – Угловые характеристики

3.2Анализ устойчивости установившегося режима

- По Ляпунову

При заданной мощности установившегося режима возможны два установившихся режима системы, соответствующие углам δ_s и δ_u. В действительности режим работы δ_u статически не устойчив и длительно существовать не может, следовательно, существует единственный устойчивый режим работы сети, причем

Для доказательства последнего утверждения необходимо проанализировать движения рассматриваемой системы при малых возмушениях установившегося режима.

Kd=10

= 56+120 т*м²

N_об=3000 об/мин

Найдем синхронизирующую мощность:

/град

Расчет корней характеристического уравнения и критерия устойчивости с учетом демпферных моментов. Корни находятся из следующего квадратного уравнения, которое получено из уравнения движения для синхронной машины.

1. Без АРВ

Корни комплексные с отрицательной вещественной частью – в установившийся режим статически устойчив.

2. С АРВ ПД

Корни комплексные с отрицательной вещественной частью – в установившийся режим статически устойчив.

3. С АРВ СД

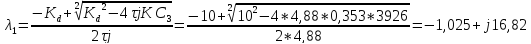
Корни комплексные с отрицательной вещественной частью – в установившийся режим статически устойчив.

- Позиционная модель

В позиционной модели режимы электрической системы зависят от положения ротора синхронного генератора. Наличие демпфирующих свойств не учитываются. В этих условиях корни характеристического уравнения зависят только от значения синхронизирующей мощности Сn.

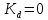
Найдем корни характеристического уравнения

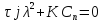
1. Без АРВ

Корни мнимые – режим устойчив.

2) C АРВ ПД

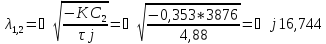
Корни мнимые – режим устойчив.

3) С АРВ СД

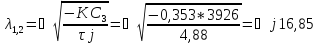
Корни мнимые – режим устойчив.

Определим запас по статической устойчивости. Для этого нужно определить максимумы угловых характеристик трех моделей СГ. Из рисунка 4 видны максимумы угловых характеристик и соответствующие им углы:

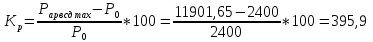
Таблица 2 – Сводная таблица характеристик статической устойчивости

Хар-ка	, град	, МВт	, МВт/град			, %	Устойчив/неустойчив
	90	3191	2148	-1,025 ±j12,423	±j12,465	32,95	Устойчив
	114,7	6369	3876	-1,025 ±j16,713	±j16,744	165,39	Устойчив
	128,8	11902	3926	-1,025 ±j16,82		395,9	Устойчив

- Критерии Михайлова

Является частотным критерием устойчивости и характеризуется простой геометрической интерпретацией, наглядностью и отсутствием ограничений на порядок характеристического уравнения.

При анализе используется линейная модель – уравнение первого приближения (малых колебаний) Для уравнения первого приближения строится годограф Михайлова – ориентировочная кривая, в комплексной плоскости, вещественное число ω меняется 0 до +∞. Допустим, что годограф Михайлова не проходит через начало координат, т.е. многочлен не имеет мнимых корней. Утверждается: для устойчивости системы необходимо и достаточно, чтобы ее годограф Михайлова делал поворот вокруг начала координат против часовой стрелки на угол n·∏/2, где n – степень полинома.

Для анализа устойчивости уравнение малых колебаний представляется в виде:

- без АРВ

Где изменяется от 0 до +∞

Таблица 2 – Результаты расчетов для построения годографа

ω	0	5	10	100	1000	1000
Re	758.244	636.244	270.244	-48041.756	-4879241.76	-4879241.76
Im	0	367.65	735.3	7353	73530	73530

- с АРВ ПД

Таблица 2 – Результаты расчетов для построения годографа

ω	0	5	10	100	1000	1000
Re	1368.228	1246.228	880.228	-47431.772	-4878631.77	-4878631.77
Im	0	17.65	35.3	353	3530	3530

- с АРВ СД

Таблица 2 – Результаты расчетов для построения годографа

ω	0	5	10	100	1000	1000
Re	1385.878	1263.878	897.878	-47414.122	-4878614.12	-4878614.12
Im	0	17.65	35.3	353	3530	3530

Построения годографа Михайлова представлены на рисунках 5,6 и 7, для СГ без АРВ, АРВ ПД и АРВ СД соответственно.

Рисунок 5 – Годограф Михайлова для СГ без АРВ

Рисунок 6 – Годограф Михайлова для СГ с АРВ ПД

Рисунок 7 – Годограф Михайлова для СГ без АРВ СД

Вектор D(jω) начинается на положительной части действительной оси, проходит 2 кванта и разворачивается в угол 180° при увеличении ω от 0 до +∞, а значит система устойчива.