
- •Рассмотрим основные свойства преобразования Фурье, которые формулируются как теоремы.
- •Теорема о сдвиге.
- •Теорема о свертке.
- •Теорема о масштабе (подобии).
- •Теорема о модуляции.
- •Теорема Парсеваля.
- •Единичная функция. (рис. 2.2)
- •Дельта–функция (рис. 2.4).
- •Частотная зависимость свойств электрической цепи может определяться различными целями. Например, для неискаженной передачи сигнала требуется, чтобы комплексная передаточная функция цепи одновременно удовлетворяла двум, рассмотренным ранее, условиям
Сравнивая схемы рис. 5.5 и рис. 5.4,б, видим, что данная схема является дифференциатором, причем постоянную времени легко определить. Находим τ = 10-3. Тогда сигнал на выходе дифференциатора будет равен производной от входного сигнала, который задан в условии ТЗ, умноженный на постоянную времени. В результате получим значение амплитуды сигнала Um= 10-3 ∙ 5∙ 30 = 150 мВ.
5.1. Коррекция и регулирование частотных характеристик
Частотная зависимость свойств электрической цепи может определяться различными целями. Например, для неискаженной передачи сигнала требуется, чтобы комплексная передаточная функция цепи одновременно удовлетворяла двум, рассмотренным ранее, условиям
H ( ) const,( ) TЗ n
Или для передачи сигнала по линии связи, требуется определенный уровень искажений амплитуды и фазы сигнала, а линия физически не обеспечивает этот уровень. В рассмотренных и других случаях можно добиться нужных свойств цепи передачи сигнала, если последовательно с корректируемой цепью включить корректирующую цепь (корректор). Различают корректоры АЧХ и корректоры ФЧХ, поскольку одним и тем же корректором линейных искажений трудно исправить амплитудные и фазовые искажения.
АЧХ цепи передачи требуемой формы можно создать с помощью корректирующей цепи, содержащей неинвертирующую или инвертирующую схемы включения ОУ.
Корректоры, по определению, имеют передаточные функции с одинаковым числом нулей и полюсов, которые, чередуясь, располагаются на отрицательной части действительной оси p-плоскости (это основной признак корректора).
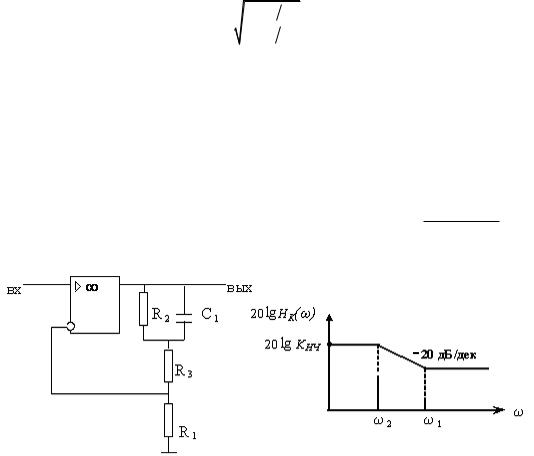
Для примера рассмотрим корректор низких частот (НЧ) первого порядка. Передаточная функция такого корректора имеет вид
HK(р)=KНЧ ∙ (1+p 1 ) (1+p 2). Соответствующая этому выражению АЧХ определяется как
26
|
H ( ) K |
1 1 |
|
|
KНЧ |
|
1 2 |
|
|
|
|
|
|
|
, |
где 1 = 1 1; |
2 = 1 2 ; |
2 |
< . |
Схема корректора НЧ первого порядка приведена на рис 5.6, там же приведена его АЧХ в логарифмическом масштабе. Из сравнения схемы рис. 5.6 и неинвертирующей
схемы 5.2 следует, что Z1=R1;Z2=R3 + R2 (1+jω 2); 2=R2 C1 .
K |
НЧ |
|
R1 R2 R3 |
, |
1 |
|
2 |
|
R1 R3 |
|
R |
|
|||||||||
|
|
|
|
R R R |
||||||
Тогда находим окончательно |
|
|
1 |
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
. |
|
Рис. 5.6 Корректор верхних частот (ВЧ) первого порядка будет иметь передаточную
функцию, также соответствующую выражению (5.2). Однако соотношение между граничными частотами 1 и 2 будет противоположным, т.е. будет 1 < 2. Тогда АЧХ будет иметь подъем 20 дБ/дек при изменении частоты от 1 до 2. Схема корректора ВЧ первого порядка получается из схемы корректора НЧ рис.5.6, если сопротивления Z1 и Z2 поменять местами.
ФЧХ можно корректировать, не изменяя АЧХ, с помощью фазовых фильтров на ОУ. Фазовым называется фильтр, АЧХ которого не зависит от частоты, а его ФЧХ зависит от частоты. У фазовых фильтров нули передаточной функции расположены на правой полуплоскости р-плоскости, а симметричные им полюсы - на левой полуплоскости. Например, передаточная функция фазового фильтра 1-ого порядка выглядит так:
H(p)=(1-p 0 (1+p 0 , где 0 0.
На рис. 5.7 приведены схема фазового фильтра (корректора) первого порядка и его частотные характеристики. Для приведенной схемы : H(p)=(1-pR1 C1 (1+p R1 C1 На НЧ емкость не влияет на работу и схема является повторителем сигнала ( = ). На ВЧ – это инвертор с единичным коэффициентом усиления ( = ). Фазовый сдвиг
27
определяется ФЧХ: = –2 arctg( R1C1 ). Для получения обратной ФЧХ (изменения фазы то до ) нужно поменять местами C1 и R1 , тогда = –2 arctg( RC ).
Лекция 6 Синтез нерекурсивных цифровых фильтров
6.1. Дискретные и цифровые сигналы
Аналоговым (непрерывным во времени) называется такой сигнал, который описывается непрерывной функцией времени. Типичным аналоговым сигналом (точнее сообщением) является речь и изображение, гармонический сигнал и др.
Дискретный сигнал задан однозначно на счетном множестве точек временной оси, т. е. описывается дискретной функцией времени. Как правило, шаг дискретизации, т.е. период следования дискретных моментов (точек), для каждого сигнала постоянен. Отсчётные значения сигнала в каждой точке могут иметь произвольную величину.
Цифровой сигнал – частный случай дискретного сигнала. Он характеризуется тем, что его отсчётные значения квантованы по величине, т.е. их можно представить числами с конечным числом разрядов (цифр). Если шаг квантования ∆k устремить к нулю, то цифровой сигнал будет эквивалентен дискретному сигналу.
Процедура дискретизации непрерывного сигнала приводит к тому, что в паузах между точками дискретизации сигнал условно считается равным нулю, т.е. его отсчёты можно
представить как произведение функции сигнала на функцию единичного импульса r(t)
sд(t) s(t)r(t kTд )
k 0
Единичный импульс имеет амплитуду равную единице и длительность стремящуюся к нулю. Поэтому такой сигнал является импульсным сигналом с бесконечно узкими импульсами. Этот импульсный сигнал представляет собой последовательность единичных импульсов, промодулированных по амплитуде непрерывным сигналом (это так называемый АИМ-сигнал). Его иногда называют решётчатым сигналом. Для удобства анализа дискретных ЭЦ такой сигнал ещё больше идеализируют и представляют в виде
28
произведения исходного сигнала s(t) на дискретизирующую последовательность h(t) , состоящую из d-функций, т.е.
η(k,t) Tд δ(t kTД )
k
,
где TД интервал дискретизации исходного сигнала.
Соответствующий импульсный сигнал описывается следующей формулой
sИ (t) Tд s(k) δ(t kTД )
k 0
,
где s(k) отсчет непрерывного сигнала в точке k.
Площадь спектральной составляющей в соответствии с фильтрующим свойством d-функции будет равна значению исходного сигнала в точке kTд. Его часто называют идеальным импульсным сигналом.
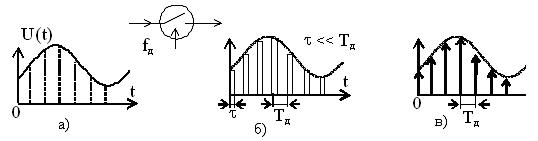
Преобразования аналогового сигнала в дискретный сигнал осуществляют с помощью ключадискретизатора как показано на рис. 6.1. Непрерывный сигнал U(t), показанный на рис.6.1,а) поступает на ключевую схему, которая с частотой дискретизации fД преобразует его в последовательность коротких импульсов рис. 6.1,б). Амплитуда этих импульсов равна значению непрерывного сигнала в отсчетных точках. Таким образом, огибающая импульсной последовательности соответствует входному непрерывному сигналу.
Рис.6.1
На рис. 6.1,в) показана временная диаграмма соответствующего импульсного сигнала. Скорость передачи дискретных значений сигнала определяется частотой дискретизации.
Пусть дискретный сигнал задан своими отсчетами при всех значениях t ³ 0, тогда для его описания можно использовать модель импульсного сигнала. Если непосредственно
29
провести вычисления по формулам прямого преобразования Фурье или Лапласа, то найдем
Sи(p) T
0 Д
|
s |
|
δ(t kT |
)e pt dt T |
|
s |
|
e |
pkT |
|
k |
|
k |
Д |
|||||
k 0 |
|
|
Д |
Д k 0 |
|
|
|
.
Это преобразование Лапласа дискретного сигнала (ряд Дирихле). Используя соотношение
p j
, можно от преобразования Лапласа перейти к преобразованию Фурье, т.е. получить спектральную плотность сигнала.
При дискретизации непрерывных сигналов стоит вопрос о выборе интервала ТД, который определяется теоремой отсчетов, носящей название “теоремы Котельникова”. Она формулируется следующим образом: Непрерывный сигнал, спектр которого не
содержит частот выше fВ , может быть полностью восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени TД =1/2fв .
Способ однозначного восстановления сигнала определяется рядом Котельникова:
|
sin[ в (t д )] |
|
1 |
|
|
||
s(t) s(k д ) |
в (t д ) |
д |
|
|
|
|
|
2 fв |
в |
||||||
k |
|
|
|||||
|
, где |
|
|
|
. |
||
Сравнивая ряд Котельникова с обобщённым рядом Фурье, рассмотренным ранее,
s(t) C(k) (k,t) k
,
можно сделать вывод о том, что в представлении рядом Котельникова используется обобщенный ряд Фурье с системой ортонормированных функций следующего вида
|
|
|
sin[в (t |
k |
|
)] |
|
|
|
|
|
||||
|
|
|
|
|
2 fв |
||
(k,t) 2 fв |
|
|
|||||
в (t |
|
k |
) |
|
|||
|
|
|
|
|
|||
|
|
2 fв |
|
||||
|
|
|
|
|
|
||
.
Именно такой сигнал имеет строго ограниченный спектр.
6.2. Преобразование формы сигналов
30
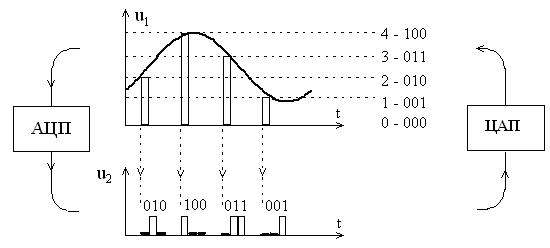
Процесс преобразования аналоговой формы сигнала в цифровую включает два этапа: дискретизацию во времени, рассмотренную в предыдущем разделе, и квантование по уровню. Если первая операция линейная, то вторая – нелинейная. Квантованные уровни сигнала соответствуют ряду чисел от нуля до максимального числа, определяемого разрядностью квантователя.
Из технических соображений числа представляются в двоичном коде (т. е. комбинацией цифр двоичного кода «0» и «1»), что объясняется достижениями микроэлектроники в разработке элементов с двумя устойчивыми состояниями. Таким образом, фрагмент соответствующего цифрового сигнала имеет вид, показанный на рис.6.2. На этом рисунке показано четыре уровня квантования непрерывного сигнала u1(t). Физически последовательность 2-х чисел отображается последовательностью уровней напряжения. Например, «1» это +5 В, «0» это 0 В. Тогда физический цифровой сигнал имеет вид, показанный на диаграмме преобразования рис. 6.2 в виде напряжения u2(t). Сигнал именно такого вида действует на входе и выходе цифровой ЭЦ. Конечно, это непрерывный, по сути, сигнал. Однако определяющим для такого сигнала является цифровой код, т. е. набор чисел - комбинаций цифр принятого кода (в частности двоичного кода).
Переходы от дискретного сигнала к аналоговому сигналу и наоборот осуществляются с помощью цифро-аналогового преобразователя (ЦАП) и аналоговоцифрового преобразователя (АЦП). Эти переходы показаны на рис. 6.2 стрелками с соответствующими структурными звеньями.
Рис.6.2
АЦП осуществляет преобразование каждого дискретного десятичного значения сигнала в двоичную систему исчисления. Например,
31
3 = 0×22 + 1×21 + 1×20 = 011.
Чем выше требуемая точность АЦП, тем больше необходимое число разрядов «n» . Тактовая частота, с которой работает АЦП, равна частоте дискретизации. Она должны удовлетворять условию
Fти 2n 1
TД
,
так как максимальный десятичный эквивалент двоичного числа будет
N10макс 2n 1
.
Цифровые сигналы характеризуются скоростью передачи, которая измеряется в бит/с. Бит - минимальное сообщение, означающее выбор одного из двух значений: "0" или "1". 1 байт равен 8 бит. На передачу сигнала через электрическую цепь со скоростью 1 бит/с обычно требуется 1 Гц полосы частот (предел Найквиста).
6.3. Аналитическое описание дискретных сигналов
Реально, при цифровой фильтрации, непрерывный сигнал s(t) описывается на интервале времени (0, Т0) совокупностью N отсчетов, следующих через интервал Tд, т.е.N=T0/Tд. Такую выборку можно считать одним периодом периодического сигнала и для ее спектрального описания применить ряд Фурье. Используем модель импульсного сигнала на периоде и представим импульсный периодический сигнал в виде ряда Фурье
|
|
|
|
|
|
|
sи (t) |
|
( jn)e |
jn 1t |
|
|
|
|
|
|
|
C |
|
||
|
|
|
|
|
|
|
|
n |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
C( jn) |
1 |
T s (t)e jn 1t dt |
|
|
||||
|
|
|
|
|||||||
|
1 |
T0 |
|
T |
|
и |
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
где |
|
; |
|
|
|
|
|
. |
|
|
Подставляя выражение для sи(t), далее находим
|
T |
Д |
|
N 1 |
|
|
jn 1kT |
Д |
С( jn) |
|
|
|
|
s |
k |
e |
|
T0 |
|
|||||||
|
|
k 0 |
|
|
|
|||
|
1 |
N 1 |
|
|
j2 n |
k |
|
|
|
N |
|||
|
|
|
s |
k |
e |
|
|
||||||
|
N k 0 |
|
|
|
||
.
Это и есть прямое дискретное преобразование Фурье (прямое ДПФ) (спектр дискретного сигнала).
Соответствующее выражение для дискретного сигнала имеет следующий вид
32

|
N 1 |
j( |
2 n |
)k |
|
|
|||
s Д (t) sk |
C( jn)e |
|
N |
|
|
n 0 |
|
|
|
.
Это обратное ДПФ. В этой формуле сумма конечна, так как дискретный сигнал содержит конечное (N) число гармоник. Период сигнала равен Т0=NТД.
Для восстановления действительного сигнала необходимо вычислить конечную сумму:
|
|
|
2 t |
|
|
|
|
|
4 t |
|
|
|
|
N |
|
N t |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
s(t) C(0) 2 |
C( j1) |
|
cos |
1 |
2 |
|
C( j2) |
|
cos |
2 |
2 |
|
C j |
|
|
cos |
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
T |
|
|
|
|
|
T |
|
|
|
|
2 |
|
|
|
T |
|
2 |
|
|
,
n arg C( jn)
где |
- фазовый угол соответствующей спектральной составляющей ряда |
Фурье. |
|
При спектральном анализе для реализации алгоритма ДПФ на ЭВМ используют быстрое преобразование Фурье (БПФ), позволяющее во многих случаях производить обработку сигналов в реальном масштабе времени.
Формула соответствующего дискретного преобразования Лапласа (ДПЛ) имеет вид:
|
pkTД |
SС(p) sk e |
|
k 0 |
|
.
sk s(kТ Д )
Во временной области такому изображению соответствует дискретный сигнал , соответствующий одному периоду (суммирование одного периода в ряде обратного преобразования Фурье).
Рассмотренные функциональные преобразования дискретного сигнала полезны с точки зрения установления связи с соответствующими преобразованиями непрерывных сигналов, но они достаточно сложны. Можно функциональные преобразования дискретных сигналов упростить, соответствующим выбором формы ряда.
Например, для функционального преобразования использовать степенной ряд комплексной переменной z , т.е. ряд следующего вида
|
|
|
|
z k |
|
|
|
s |
|
s |
2 |
|
|
Sc(z) |
|
s |
k |
s |
0 |
|
1 |
|
|
|
|
||
z |
z 2 |
|
|||||||||||
|
k 0 |
|
|
|
|
|
|
|
|||||
Это Z-преобразование дискретного сигнала. Обозначим далее |
S(z) Z (sk ) |
||||||||||||
. |
|||||||||||||
Очевидно, степенной ряд должен быть сходящимся, чтобы существовало
33

Z-преобразование. Для конечного числа отсчетов сумма будет конечной и существование Z-преобразования будет обеспечиваться автоматически.
Обратное Z-преобразование дается следующей формулой
sk 1 |
Sc(z)z k 1dz. |
|
2πj |
|
|
Составлены таблицы Z-преобразований. Сравнивая формулы ДПЛ и Z-преобразования, |
||
|
e pTД |
Z |
находим, что они будут совпадать при условии |
, т.е. когда Z-преобразование |
|
определяется на единичном круге. Поэтому часто Z-преобразование рассматривают, как переход от переменной «p» к переменной Z=ерТД в дискретном преобразовании Лапласа. При этом p-плоскость переходит в Z-плоскость, как показано на рис. 6.3. Левая р-полуплоскость переходит в круг единичного радиуса, а правая р-полуплоскость во всю остальную часть Z-плоскости. Действительно, используя формулу Эйлера, можно получить
z e pTД |
еσТ Д е jωωД |
еσТ Д ( cosωT |
Д |
sin ωT |
Д |
) |
|
|
|
|
. |
||
|
|
|
|
|
|
j |
|
Z-плоскость |
|
р-плоскость |
|
|
|
|
|
|
|
0 |
j |
1 |
|
Ось |
|||
|
|||
|
Рис. 6.3 |
|
|
0 |
Если |
(устойчивые системы), то Z лежит внутри единичного круга. Именно поэтому |
единичный круг имеет важное значение при исследовании дискретных ЭЦ. Рассмотрим для примера решения нескольких тестовых заданий.
ТЗ№1.
Комплексная переменная Z-преобразования связана с переменной преобразования Лапласа зависимостью … .
а) z= 1/epТД, б) lnz=pTД, в) z= epTД, г) z= epTД, д) z=pTД,
34

Решение основано на знании соотношения между переменными преобразования Лапласа и Z-преобразования z=ерТД . Тогда правильный ответ будет б) и г).
ТЗ№2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
j |
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||||||||
Точка р-плоскости pi= … соответствует точке Z-плоскости zi= |
|
|
|
|
|
|
|
|
, если |
|
||||||||||||||||||||||||||||||||||||
интервал дискретизации Тд=1с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
1 |
j |
1 |
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
j |
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
б) 0+j 4 |
|
1+j, |
|
|
|
|
|
, д) 0+j |
4 |
|
|
|
|
|
|||||||||||||||||||||||||||||
а) j, |
|
, в) |
|
г) |
|
|
|
, |
е) - |
|
|
|
|
|
|
|
|
Решение |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z е ТД (cosωT |
|
sin ωT |
) |
|
|||||||||||||||||||||
основано на знании двух соотношений: р=σ+jω и |
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
Д |
. Тогда |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
из второго равенства для точки на Z-плоскости zi= |
|
|
|
|
|
|
находим |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
- |
1 |
|
е ТД cosωTД |
|
1 |
|
е ТД sinωTД |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д 1 |
||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
||||
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
. Из этих уравнений находим |
|
и |
|||||||||||||||||||||||
cosωT |
- |
1 |
|
sin ωT |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Д |
2 |
|
; |
Д |
|
, при условии ТД=1с. Отсюда легко получить, что σ = 0, а |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = |
|
, т.е. рi = 0+j |
. Таким образом, правильный ответ будет д). |
|
Конечно, можно, |
|||||||||||||||||||||||||||||||||||||||||
найдя условие σ = 0, сразу для рассмотрения оставить два конкурирующих ответа б) и д), так как только у них σ = 0.
6.4. Аналитическое описание цифровых электрических цепей
Центральной задачей обработки цифровых сигналов является цифровая фильтрация, которая осуществляется цифровым фильтром (ЦФ). ЦФ – является частным случаем цифровой ЭЦ. Таким образом, ЦФ – это цифровая ЭЦ, осуществляющая цифровую фильтрацию сигнала. Далее будем рассматривать только линейные ЦФ с
35
постоянными параметрами, т. е. стационарные линейные ЦФ, которые для краткости будем называть просто «ЦФ».
В рамках основ теории ЭЦ в качестве оценки сигнала при обработке принимается линейный оператор - свертка входного сигнала и импульсной характеристики цепи. Таким образом, свертка определяет линейную фильтрацию сигнала. Поскольку по определению фильтр осуществляет фильтрацию сигнала, то часто фильтром называют все, что осуществляет свертку, т.е. это может быть и схемотехническое устройство, и вычислительный процесс (программа).
Аналогия Z-преобразования и дискретных преобразований Фурье и Лапласа позволяет использовать основные методы анализа непрерывных ЭЦ применительно к исследованию цифровых ЭЦ. Рассмотрим основные из этих методов.
Временной метод связан с таким понятием как импульсная характеристика. Импульсной характеристикой ЦФ называется его реакция на единичный импульс r (k) и обозначается h(k). Единичный импульс определяется следующим образом: если k=0, то r (k)=1, если k>0, то r (k)=0. Отсюда следует, что для физически реализуемого ЦФ
h(k) h(kTД ) 0
при k<0. Тогда, используя понятие дискретной свертки, находим сигнал
|
|
|
|
h(k) |
|
на выходе ЦФ с импульсной характеристикой |
: |
||||
|
N 1 |
N 1 |
|
|
|
s2(k) |
s1(m) h(k m) |
s (k-m) h(m) |
|||
|
|||||
|
m 0 |
m 0 |
1 |
, |
|
|
= |
|
|
||
где s1(∙) и s2(∙) сигнал на входе и выходе фильтра.
Переходная характеристика ЦФ - g(k) это его реакция на дискретную единичную функцию 1(k).
Частотный метод связан с таким понятием как комплексная передаточная функция. Комплексная передаточная функция цифрового фильтра H(jn) это отношение дискретного преобразования Фурье (ДПФ) сигнала (спектра дискретного сигнала) на выходе C2(jn) к дискретному преобразованию входного сигнала C1(jn), т.е.
H(jn) = C2(jn) / C1(jn).
Далее, находим
H |
N 1 |
j2 n |
k |
|
|
||||
( jn) h(k)e |
|
N |
||
|
k 0 |
. |
||
|
|
|||
36

Таким образом, комплексная передаточная функция цифрового фильтра H(jn) равна дискретному преобразованию Фурье от его импульсной характеристики.
Операторный метод связан с таким понятием как передаточная функция ЦФ. Передаточная функция цифрового фильтра H(z) это отношение Z-преобразований выходного сигнала S2(z) к входному сигналу S1(z), т.е.
H(z) = S2(z) ∕ S1(z).
По аналогии можно сделать вывод, что передаточная функция цифрового фильтра H(z) равна Z- преобразованию от его импульсной характеристики
N 1 k
H (z) h(k)z
k 0
.
Используя полученные формулы, можно эффективно исследовать и установившийся и переходный режимы работы цифровых фильтров.
В качестве примера решения тестовых заданий рассмотрим наиболее типичное ТЗ. Например, необходимо определить выходное напряжение дискретной цепи с импульсной характеристикой рис. 6.4, если входное напряжение задано.
h(k) |
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
k |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.4 Решение основано на знании формулы дискретной свертки. Тогда сигнал на выходе
дискретной цепи с известной импульсной характеристикой (эта характеристика приведена в виде графика) определяется по формуле свертки
u |
|
(k) |
1 |
u (k-m) h(m) h( 0 ) u |
|
(k) h(1) u |
|
(k 1) |
|
|
|
|
|||||
|
вых |
|
m 0 |
вх |
вх |
|
вх |
|
.
В тестовом задании требуется найти коэффициенты перед членами uвх(∙). Они определяются значениями импульсной характеристики h(0) и h(1). Из графика импульсной характеристики видно, что эти коэффициенты будут равны 2 и -1.
37

6.5. Нерекурсивные цифровые фильтры
Физически реализуемые алгоритмы дискретной фильтрации для формирования выходного дискретного сигнала могут использовать лишь предыдущие входные и выходные отсчеты.
Если для формирования выходного сигнала используются лишь отсчеты входного сигнала, такой алгоритм называется нерекурсивным. Если для формирования выходного сигнала используются отсчеты и выходного сигнала, то такой алгоритм называется рекурсивный. «Рекурсия» (лат. recursus – возврат, обратный путь) – циклическое обращение к данным (к сигналу) полученным на предшествующих этапах фильтрации. Иногда вместо слов «рекурсивный – нерекурсивный» используют равнозначные им термины «рекурентный – нерекурентный».
Вид алгоритма фильтрации приводит к определенным свойствам импульсной характеристики ЦФ. Нерекурсивность алгоритма приводит к тому, что ЦФ имеет конечную импульсную характеристику. Поэтому очень часто нерекурсивные фильтры называются «КИХ – фильтрами». Рекурсивные алгоритмы приводят к бесконечным импульсным характеристикам фильтра. Поэтому рекурсивные фильтры часто называют «БИХ – фильтрами»
Сигнал на выходе КИХ-фильтра во временной области определяется формулой дискретной свертки (формула (40.1)). Для определения структуры фильтра воспользуемся Z – преобразованием. Определим передаточную функцию КИХфильтра, как Z – преобразование импульсной характеристики (формула (40.6)).
Полученную передаточную функцию КИХ-фильтра можно представить в виде дробнорациональной функции следующим образом
N 1 |
N 1 |
H(z) h(k)z k |
h(k)z k |
k 0 |
k 0 |
|
|
|
N 1 |
z |
N 1 |
|
h(k)zN (k 1 ) |
|
|
k 0 |
|
z N 1 |
|
z N 1 |
|
.
Число (N-1) определяет порядок КИХ-фильтра. Таким образом, системная функция КИХфильтра порядка (N-1) имеет в точке Z=0 (N-1)-кратный полюс и (N-k+1) нулей, расположенных в пределах единичного круга. Поскольку других полюсов нет, КИХфильтр структурно устойчив (при любых параметрах, его полюсы всегда лежат в пределах
Z*i 1
единичного круга, т.е. |
). |
38
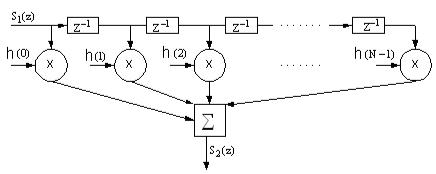
Алгоритм функционирования КИХ-фильтра можно представить в виде структурной схемы, соответствующей рассмотренной передаточной функции и представленной на рис. 6.5.
Рис. 6.5 Из формулы взвешенного суммирования следует, что в линейных ЦФ над сигналом
осуществляется три основных операции: сложение, умножение и сдвиг во времени на целое число интервалов дискредитации TД. Все эти операции представлены в структурной схеме соответствующими элементами. Представленная структура своей конфигурацией объясняет, почему КИХ-фильтры иногда называют трансверсальными, т.е. поперечными. Действительно, входной сигнал распространяется по цифровой линии задержки, а выходной сигнал формируется из поперечных отводов.
Определим частотные характеристики КИХ-фильтров. Поскольку АЧХ и ФЧХ – это модуль и аргумент комплексной передаточной функции, то для их определения необходимо сначала найти ее.
Поскольку комплексная передаточная функция определяется как преобразование Фурье от импульсной характеристики, то ее можно также определить из передаточной функции,
Z e |
j TД |
|
|
|
путем замены переменной |
|
. Находим |
|
|
H(jω( |
N 1 |
j kT |
Д |
|
h(k)e |
|
|||
|
|
k 0 |
|
|
.
Если использовать ДПФ, тогда получим
H(jn) N 1h(k)e jknω1TД
k0
.
Таким образом, при заданном интервале дискретизации из этих формул можно получить достаточно разнообразные выражения для комплексной передаточной функции в
39
зависимости от вида импульсной характеристики ЦФ. Соответствующие АЧХ и ФЧХ описываются следующими выражениями:
H(ω( N 1h(k)e j kTД
k 0
;
φ(ω) arctg Im H(jω) Re H jω
.
Из этих формул следует, что АЧХ и ФЧХ цифрового фильтра являются периодическими
|
2 /TД |
функциями. Период равен величине |
, т.е. он определяется интервалом |
дискретизации ТД. |
|
Рассмотрим методику решения тестовых заданий на следующем примере. Передаточная функция дискретной цепи равна … , если ее структурная схема задана на рис. 6.6
z-1 |
+ |
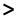 2
2
Рис. 6.6 Решение основано на знании определения и основных свойств передаточной
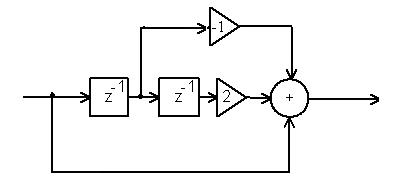
функции дискретной цепи. Если на входе действует S1(z), то на выходе будет S2(z)=H(z)S1(z). Используя структурную схему цепи можно найти S2(z)=2∙ S1(z)+ z-1∙S1(z)= S1(z)∙(2+z-1). Из сравнения с предыдущей формулой находим H(z)= 2+z-1. Конечно, имея определенный опыт в чтении структурных схем, можно непосредственно по схеме найти этот ответ.
Лекция 7 Синтез рекурсивных цифровых фильтров
Сигнал на выходе БИХ-фильтра во временной области определяется формулой дискретной свертки
s2(k) s1(m)h(k m) m 0
.
40

Однако, поскольку алгоритм рекурсивный, то для формирования k-го отсчета выходного сигнала используются предыдущие значения входного и выходного сигналов. Соответствующее разностное уравнение БИХ-фильтра будет иметь следующий вид: s2(k) b0 s1(k) b1s1(k 1) bm s1(k m) a1s2(k 1) an s2(k n)
Коэффициенты a1, a2, … an определяют рекурсивную часть алгоритма и не равны нулю одновременно. Обычно n ≥ m. Выполняя Z-преобразование алгоритма рекурсивной фильтрации,находим:
|
|
m |
b |
z k S |
|
n |
a |
|
z k |
S (z) S (z) |
2 |
(z) |
k |
||||||
2 |
1 |
k 0 |
k |
|
k 1 |
|
|
||
.
Это и есть алгебраизация разностного уравнения (42.2) с помощью Z-преобразования.
Определим передаточную функцию рекурсивного ЦФ, пользуясь определением
(40.5)
Получим
m b z k k k
H(z) 0
1 n a z k k 1 n
.
Число «n» определяет порядок БИХ-фильтра. Анализ передаточной функции рекурсивного фильтра показывает, что она на Z-плоскости имеет «n» - полюсов. Если эти полюсы размещаются на Z-плоскости в пределах единичного круга, то рекурсивный цифровой фильтр – устойчив. Если хотя бы один полюс выйдет за пределы единичного круга, то рекурсивный ЦФ будет неустойчив. (Если будет располагаться на границе, то ЦФ будет автоколебательной системой). Полученные выражения позволяют построить структурную схему рекурсивного ЦФ, приведенную на рис. 42.1.
41

S |
1 ( z ) |
|
|
Z 1 |
|
Z 1 |
|
|
Z 1 |
|
|
Z 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b |
0 |
X |
|
b 1 |
X |
b |
2 |
X |
|
|
|
|
b m |
X |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S 2 ( z ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
a |
n |
|
|
|
|
X |
a |
2 |
X |
a |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Z |
1 |
|
|
|
|
Z |
1 |
|
Z |
1 |
|
Рис. 7.1
Из полученной схемы видно, что верхняя часть соответствует нерекурсивной части алгоритма фильтрации, а нижняя – рекурсивной. Это схема прямой реализации алгоритма ЦФ. Из анализа структурной схемы дискретной цепи следует, что БИХ-фильтр имеет цепь обратной связи, т.е. для него принципиальным является оценка устойчивости. Для реализации рекурсивного ЦФ на элементах цифровой электроники, как это следует из схемы рис.7.1, требуется, например, два регистра сдвига и два запоминающих устройства
|
ak ;bk |
для хранения коэффициентов |
, а также две логические матрицы для умножения. |
Естественно такой фильтр может быть реализован на микропроцессоре, запрограммированном в соответствии с алгоритмом фильтрации. Можно получить некоторую экономию в необходимом объеме оперативной памяти, если перейти к канонической структуре ЦФ, где регистр сдвига используется и для сигнала прямой передачи, и для сигнала обратной связи.
Такая каноническая структурная схема рекурсивного фильтра приведена на рис.7.2.
|
|
|
S2 (z) |
|
|
|
|
|
|
|
|
|
|
b0 |
b |
|
b |
m |
|
|
X |
1 |
X |
|
X |
|
|
|
|
|
|
|||
|
Z 1 |
Z 1 |
Z 1 |
|
Z 1 |
|
|
a1 |
X |
|
|
an |
X |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
S1(z) |
|
|
|
42
Рис.7.2 Анализ канонической схемы показывает, что для ее реализации требуется лишь
один регистр сдвига (уменьшение необходимой оперативной памяти микропроцессора). Определив системную функцию БИХ-фильтра, можно найти импульсную
характеристику, взяв обратное Z-преобразование g(k) 21πj H(z)zk 1dz.
Вычисление контурного интеграла осуществляется по единичной окружности, внутри которой располагаются полюсы устойчивого БИХ-фильтра.
В качестве примера решения тестового задания рассмотрим типичное ТЗ. Необходимо определить передаточную функцию заданной на рис. 7.3 структурной схемы дискретной цепи
Рис. 7.3
На рис. 7.3 приведена структурная схема БИХ – фильтра, поскольку имеется цепь прямой передачи и цепь обратной связи, т.е. алгоритм фильтрации будет рекурсивным
S |
|
1 |
b |
z k S |
|
1 |
a |
|
z k |
(z) S (z) |
2 |
(z) |
k |
||||||
2 |
1 |
k 0 |
k |
|
k 1 |
|
|
||
,
причем b0 =1, b1 =2, a1=3.
Тогда передаточная функция будет дробно-рациональной функцией, у которой числитель описывает нерекурсивную часть алгоритма, а знаменатель – рекурсивную. Из схемы можно легко определить числитель и знаменатель передаточной функции в следующем виде
H (Z ) 1 2 Z 1
1 3 Z 1
.
7.1. Основы синтеза цифровых фильтров
43
Выражения для системных (передаточных) функций КИХ и БИХ фильтров позволяют получить самые разнообразные частотные характеристики фильтров. Однако необходимо учитывать, что принципиально невозможно создать ЦФ, частотные характеристики которого в точности повторяли бы характеристики аналогового фильтрапрототипа (АФ-прототипа). Это объясняется тем, что АЧХ и ФЧХ ЦФ являются периодическими функциями частоты, причем период определяется интервалом
|
TД |
TД |
дискретизации по времени |
. В то же время, можно так выбрать интервал |
, что |
интервал частот аналоговой цепи преобразуется в отрезок частоты цифровой цепи при |
||
|
|
З |
|
|
|
|
|
Т Д |
|||
|
|
|
|
||
сохранении общего вида АЧХ и ФЧХ. Это условие следует из теоремы отсчетов: |
|
, |
|||
|
З |
|
|
|
|
где |
- верхняя частота (частота задерживания) АФ – прототипа. Однако, если |
|
|
|
|
необходимо использовать фильтр для фильтрации сигнала из помех или разделения |
|
|
|
||
сигналов по частоте, то частота дискретизации должна определяться верхней частотой |
|
|
|||
сигнала или помех. В противном случае помехи попадут в следующий период АЧХ |
|
|
|
||
цифрового фильтра. Далее, если известна операторная передаточная функция АФ- |
|
|
|
||
прототипа H(p), то заменой переменной |
Z exp(pTД ) |
|
|
|
|
можно получить передаточную |
|||||
(системную) функцию БИХ фильтра. Для этого в выражении H(p) необходимо подставить
p |
1 |
ln z |
|
||
|
Т Д |
|
.
Однако реализовать такую системную функцию с помощью структуры БИХ фильтров не удастся, поскольку они имеют дробно-рациональные передаточные функции, а замена переменной даст трансцендентную функцию, так как H(p) также дробнорациональная функция.
ωЗТ Д |
|
Если частота дискретизации выбрана правильно, т.е. |
, то можно воспользоваться |
билинейным преобразованием: |
|
44
|
|
|
|
p |
1 z 1 |
, |
|
|
|
|
|
1 |
z 1 |
||
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
tg( |
fП |
) |
|
|
|
|
|
|
|
|
||||
|
|
f Д |
|
|
|
||
где γ = |
|
|
, fП – полоса пропускания АФ-пототипа, fД –частота дискретизации. |
||||
Билинейное преобразование приведет к тому, что, во-первых, частотные характеристики АФ-прототипа и ЦФ будут совпадать, а, во-вторых, системная функция будет дробнорациональной. Приближение будет тем точнее, чем меньше ωТД, т. е. на низких частотах и при достаточно малом интервале дискретизации ТД. Именно при этих условиях характеристики АФ и ЦФ будут совпадать. Если воспользоваться билинейным преобразованием без учёта ограничений “теоремы отсчётов” (теоремы Котельникова), то проведённый синтез может не дать требуемого результата. Это объясняется тем, что реальные фильтры-прототипы имеют непрерывную АЧХ во всём диапазоне частот. Поэтому теоретически всегда АЧХ синтезированного ЦФ будет отличаться от непрерывной АЧХ прототипа, особенно в области верхних частот из-за эффекта перекрытия.
Таким образом, процедура синтеза ЦФ состоит в том, что в передаточной функции аналогового фиьтра-прототипа осуществляется замена переменной по формуле билинейного преобразования. Полученная системная функция будет дробно-рациональной и позволяет использовать структуру КИХ или БИХ фильтра для технической реализации цифрового фильтра.
Синтез КИХ-фильтров, отличающихся большим быстродействием по сравнению с БИХ-фильтрами, чаще основан на методе инвариантности импульсной характеристики. Поскольку АФ-прототип имеет бесконечную во времени убывающую импульсную характеристику, то задача синтеза заключается в правильном ограничении числа отсчетов характеристики N в выражении H(z). Ограничение числа отсчетов импульсной характеристики эквивалентно ее умножению на функцию “окна”. В простейшем случае это может быть прямоугольная функция, которая приводит к простому ограничению числа отсчетов. Однако в этом случае возникают искажения АЧХ фильтра (эффект Гиббса), что приводит к уменьшению ослабления в полосе задерживания фильтра. Поэтому необходимо применять функции “окна” без разрыва непрерывности, например, функцию Хэмминга
45
0,5[1 cos( |
2πk |
|
)],если 0 k N-1иW(t) 0, если k N-1 |
|
N 1 |
||||
W(t)= |
. |
|||
|
|
|||
Тогда импульсная характеристика быстродействующего ЦФ в формуле будет определяться
|
h(k) W (k) |
|
как |
. |
|
|
В качестве примера решения тестового задания рассмотрим типичное ТЗ. |
|
Необходимо определить передаточную функцию и структуру цифрового фильтра, |
||
имеющего импульсную характеристику: |
|
|
|
h(k)={1;-1;2} |
|
|
Используя выражение для передаточной функции находим |
|
|
2 |
|
|
H (Z) h(k) Z k |
1 Z 1 2Z 2 |
k 0
Этой передаточной функции соответствует структурная схема, приведенная на рис. 7.4
Рис. 7.4
Тема 3. Цепи с распределенными параметрами
Лекция 8.
Анализ процессов в длинных линиях
Линией называют пару проводов, соединяющих источник с приемником сигнала, предназначенных для передачи энергии сигнала на расстояние. Это важный частный случай цепей с распределенными параметрами. Длинной называют линию, длина которой соизмерима с длиной волны передаваемого сигнала. Часто линию, по которой
46
осуществляется передача энергии высокочастотных колебаний от генератора к нагрузке, называют фидером (название происходит от английского глагола to feed – питать). В современных устройствах связи находят применение фидеры различных типов. Воздушная линия конструктивно состоит из двух параллельных неизолированных проводов, а кабельная линия образуется парой изолированных проводов либо параллельных, либо скрученных друг с другом. Коаксиальная линия образуется полым цилиндром и центральным проводом. Пространство между ними обычно заполняется диэлектриком. Технологичностью отличается полосковая линия, состоящая из проводящих полос разделенных диэлектриком.
В диапазоне декаметровых и более длинных волн для передачи энергии обычно используется воздушная двухпроводная линия. При передаче гармонических сигналов по воздушным линиям связи без потерь фазовая скорость волн практически равна скорости
|
c 3108 м |
V 2 108 м |
|
|
с |
ф |
с |
света в вакууме |
, а при наличии потерь лишь немного меньше: |
|
. |
|
Zв 400...1500 |
|
|
Среднее значение волнового сопротивления для воздушных линий |
|
Ом. |
|
Однако на более коротких волнах воздушная линия начинает интенсивно излучать электромагнитное поле в окружающее пространство; возрастают также тепловые потери в проводах. В дециметровом диапазоне волн наиболее широко применяется коаксиальная линия передач. В кабелях фазовая скорость волн в 2…2,5 раза меньше скорости света в
|
Zв 50...75 |
вакууме. Среднее значение волнового сопротивления для кабелей |
Ом. В |
отличие от двухпроводной линии коаксиальная линия не имеет потерь на излучение, так как её электромагнитное поле отделено от внешнего пространства надёжным экраном – оболочкой внешнего цилиндрического проводника. Коаксиальный фидер обладает меньшими тепловыми потерями также оттого, что образующие его проводники имеют достаточно большие поверхности.
На сантиметровых волнах в качестве фидера используется волновод, представляющий собой полую металлическую трубу прямоугольного сечения, в которой распространяются электромагнитные волны. Отсутствие в волноводе внутреннего проводника уменьшает расход энергии на нагревание и, следовательно, уменьшает потери энергии сигнала при передаче.
47
Для анализа процессов, происходящих в длинных линиях, их представляют состоящими из элементарных участков. Эквивалентная схема участка линии длиной dх представлена на рис.8. 1
|
di |
|
|
|
|
|
|
i |
i dx |
dx |
|
L0 dx |
R0 dx |
|
|
u |
u du |
dx |
|
|
C0 dx |
G0 dx |
|
|
|
dx |
|
|
|
|
|
x 

 dx
dx 

Рис. 8.1 На эквивалентной схеме рис. 23.1 обозначены так называемые первичные
параметры длинной линии L0 [Гн/км], R0 [Ом/км], C0 [Ф/км], G0 [См/км] (они еще называются погонными или километрическими). Значения первичных параметров, как правило, гостированы и, например, для двухпроводной линии обычно составляют следующие величины L0 единицы [мГн/км], R0 сотни [Ом/км], C0 десятки [нФ/км], G0 сотые доли [мкСм/км]. Зная величину километрических параметров, легко найти параметры линии передачи сигнала, если известна ее длина. Значение первичных параметров зависит от частоты сигнала. Сильнее всех от частоты зависят резистивные параметры линии (R0, G0), что объясняется ростом потерь энергии сигнала от частоты при его распространении по линии. Потери связаны с поверхностным эффектом (скинэффектом) и потерями в диэлектрике.
Далее будем рассматривать однородные линии, у которых значение первичных параметров неизменны на всей длине.
Представление длинной линии в виде суммы элементарных участков (рис. 8.1) позволяет найти распределение тока и напряжения вдоль линии. Используя законы Кирхгофа, можно записать уравнения для напряжения и тока для элементарного участка, считая его обычной электрической цепью с сосредоточенными параметрами.
u R0i L0 ix t
, |
(8.1) |
i G0u C0 ux t
.
48

Это, так называемые, телеграфные уравнения длинной линии, определяющие изменения тока и напряжения вдоль линии. Они являются дифференциальными уравнениями в частных производных для мгновенных значений тока i(x,t) и напряжения u(x,t).
Для режима гармонических колебаний, когда на входе линии действует источник гармонического сигнала, телеграфные уравнения (8.1) в символической форме записи будут иметь следующий вид
|
dU |
R j L I |
|
d I |
G j C U |
||||
dx |
dx |
||||||||
|
0 |
0 |
|
0 |
0 |
|
|||
|
|
|
|
|
|||||
|
|
|
, |
|
|
|
|
. |
|
Эти уравнения определяют распределение комплексных значений напряжения и тока вдоль линии. Они являются обыкновенными дифференциальными уравнениями. Поэтому решение телеграфных уравнений в символической форме находится просто и имеет в общем случае следующий вид
|
|
|
I |
A1 |
e x |
A2 |
e x |
|
|
U |
|
|
|
|
|||
|
A1e x A2e x |
, |
Z B |
Z B |
(8.2) |
|||
|
|
|
|
|
. |
|||
Вполученных решениях введены обозначения
 R0 j L0 G0 j C0
R0 j L0 G0 j C0
,
Z B |
R0 j L0 |
G0 j C0 |
.
Как видно в выражении (8.2) установившиеся напряжение и ток в произвольном сечении “x ” состоят из суммы двух одинаковых по форме составляющих, отличающихся знаком в показателе экспоненты.
Введенные обозначения определяют вторичные параметры линии, причем
Z B
является коэффициентом распространения, а - волновым сопротивлением линии.
j |
|
|
||
Используя алгебраическую форму записи, получим |
|
|
, |
где - коэффициент |
|
|
|
||
ослабления (потерь), [дБ/км], - коэффициент фазы, [рад/км]. |
|
|
||
49
|
|
|
Их типовые значения |
= 0,1 5 [дБ/км], |
= − 5 10-6 [рад/км]. |
Физический смысл вторичных параметров заключается в следующем: волновое сопротивление характеризует отношение комплексного напряжения к комплексному току волны, а коэффициент распространения характеризует изменение мощности волны, при прохождении ею единицы длины линии.
8.1. Отражение волн на конце линии и режим бегущих волн
Напряжение и ток в любой точке линии можно рассматривать как результат наложения двух волн: падающей и отраженной, как это следует из выражения (8.2). Если знак в показателе экспоненты отрицательный, то увеличение “x” означает движение волны от начала линии (x=0) к концу (x=l). Если знак в показателе экспоненты положительный, то волна движется от конца к началу линии. Таким образом, падающая волна распространяется от источника к нагрузке. Обозначая напряжение падающей волны символом “+”, находим
|
U A1e x |
u |
2A1e x cos t x 1 |
||
|
|
, |
|
|
. |
Отраженная волна распространяется от нагрузки к источнику. |
|||||
U A2e x |
u |
2A2e x cos t x |
2 |
||
|
, |
|
|
|
. |
Распространение волн можно проследить, отслеживая координаты точек равной |
|||||
фазы, как показано на рис. 8.2 для двух моментов времени |
|
||||
u+ |
t1 t2 |
|
|
t2 |
u- |
|
|
|
|
t1 |
|
x=0 |
|
|
x |
x |
x=l |
|
|
|
|
||
|
|
|
|
t2>t1 |
|
|
Падающая |
|
Отраженная |
||
Рис. 8.2
При фиксированном расстоянии x каждая волна является гармонической функцией времени. Направление распространения волн показано на рис. 8.2 стрелками. Амплитуда напряжения уменьшается по мере распространения волны. Степень уменьшения определяется коэффициентом ослабления α. Фазовая скорость распространения - скорость перемещения точек колебаний равной фазы определяется, если взять производную от
50
|
|
|
|
dt dx 0 |
полной фазы (аргумент “cos”), считая ее постоянной |
, |
|||
V |
dx |
|
|
|
ф |
dt |
|
|
|
.
Таким образом, фазовая скорость пропорциональна частоте сигнала. Однако, коэффициент фазы также пропорционален частоте. Поэтому фазовая скорость практически не зависит от частоты сигнала, а определяется первичными параметрами линии.
Можно рассматривать линию как четырехполюсник, что представлено на рис. 24.2
I1 |
I 2 |
|
|
I 1 |
|
I 2 |
U 1 |
|
U 2 |
|
U 1 |
l |
U 2 |
|
Z B |
|||||
|
|
|
|
|
||
|
|
|
|
|
|
l
Рис.8.3 Уравнение передачи длинной линии можно представить в гиперболической, более
компактной форме, если определить постоянные интегрирования А1 и А2 из граничных условий в начале или в конце линии
U 1 ch l U 2 Z B sh l I 2
,
I1 sh l U 2 ch l I 2
По форме эти уравнения соответствуют уравнениям передачи четырехполюсника в A – параметрах.
Из теории четырехполюсников известно, что значение напряжения и тока зависят от степени его согласования по входу и выходу. Поэтому в нагруженной линии распределение напряжения и тока будет определяться не только волновыми параметрами, но и степенью согласования. Степень согласования длинной линии характеризуется коэффициентом отражения, который равен отношению комплексных амплитуд напряжений (или токов) отраженной и падающей волн в произвольном сечении. Найдем выражение для коэффициента отражения в произвольном сечении
51

u (x) A2 e2 x
A1
Используя граничные условия в конце линии x=l, U(l) = U2 , I(l) = I2, можно определить постоянные интегрирования и найти коэффициент отражения в следующем виде
|
u |
(x) |
U 2 Z B I 2 |
e 2 |
|
(l x) |
||
|
||||||||
|
|
|
U |
2 Z B I 2 |
|
|
|
|
|
|
|
Z B Z H |
|||||
|
|
|
|
|
Z Г |
|||
В режиме согласованного включения |
|
|
в линии распространяется только |
|||||
падающая волна. Такой режим называется режимом бегущей волны и является предпочтительным, поскольку вся энергия падающей волны остается в нагрузке. В этом случае коэффициент отражения будет равен нулю. Входное сопротивление линии в режиме бегущих волн равно волновому сопротивлению. Если линия имеет потери, то амплитуда тока и напряжения в этом режиме убывает по экспоненциальному закону с увеличением расстояния х. Поэтому для лучшей передачи энергии сигнала нужно брать линию как можно короче. Если линия без потерь, то величина тока и напряжения от расстояния не зависят.
В случае режима бегущей волны уравнения передачи упрощаются и имеют
U1 |
|
I1 |
e |
|
l . |
|
|
||||||
I 2 |
||||||
U 2 |
|
|
|
|
следующий вид
При наличии рассогласования на входе и выходе в линии образуются потоки падающих и отраженных волн
Наличие отражений искажает передаваемый сигнал, поэтому на практике коэффициенты отражений на входе и выходе реальных линий строго нормируются. Значения этих коэффициентов определяется как
(0) |
(Z Н Z B ) |
e 2 |
|
l |
(l) |
(Z H Z B ) /(Z H Z B ) |
|
|
|||||||
(Z Н Z B ) |
|||||||
|
|
, |
|
. |
|||
52

Таким образом, модуль коэффициента отражения растет по мере увеличения х и достигает наибольшего значения в конце линии.
Лекция 9 Линии без искажений и использование отрезков длинных линий
Линией без потерь называют линию, в которой можно пренебречь рассеянием энергии. В этом случае резистивные первичные параметры будут равны нулю, т. е.
R0 0,G0 0
. Тогда вторичные параметры будут определяться следующими соотношениями
0 ,  L0C0 2 / ZВ
L0C0 2 / ZВ 
 L0
L0 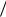 C0
C0
|
, |
. |
|
|
Z н |
|
|
В зависимости от типа нагрузки |
на конце линии различают следующие режимы |
||
работы: линия с разомкнутыми выходными зажимами |
(Zн ) |
||
|
,линия с замкнутыми |
||
(Z н 0) |
|
|
|
накоротко выходными зажимами |
, подключение к линии реактивной нагрузки |
||
(Z н jX н ) |
|
|
(Zн Zв) |
, подключение к линии согласованной нагрузки |
, подключение к |
||
(Zн Zв ) |
|
|
|
линии несогласованной нагрузки |
. |
|
|
Рассмотрим распределение напряжения и тока вдоль линии при различных режимах работы. Используя выражение для коэффициента отражения в конце линии, можно определить его модуль для произвольного сечения в общем случае
(x) (x) (l) e 2 (l x)
53
Рис. 9.1 Для первых трех случаев значений нагрузки модуль коэффициента отражения в
конце линии будет равен единице, поскольку в линии отсутствуют потери, а для этих
(l)
случаев = 1. Тогда амплитуды отраженной и падающей волн будут одинаковы и в линии возникнет, так называемый, режим стоячих волн. Таким образом, режим стоячих волн может возникнуть только в линии без потерь при холостом ходе, коротком замыкании и реактивной нагрузке.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Z н ) |
I 2 0, |
В режиме холостого хода, т.е. когда линия на конце разомкнута |
, |
||||||||||||||||||||||||||||||||||
находим мгновенные значения напряжения и тока: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
u |
|
|
( y, t) |
|
U |
|
|
|
|
|
|
|
|
|
|
|
y |
|
cos(t) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
х.х. |
|
2 |
|
2 |
cos(2 |
|
) |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
U 2 |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
i |
|
|
(y,t) |
|
|
2 |
|
|
|
|
|
|
|
|
|
cos(t |
|
|
|
|
|
|||||||||
|
|
|
|
|
х.х. |
|
|
|
|
|
sin(2 |
|
|
|
|
) |
|
90 ) |
|
||||||||||||||||
|
|
|
|
|
|
|
Zв |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действующие |
значения |
|
напряжения и |
|
тока |
в |
|
|
|
|
2 |
раз |
|
меньше амплитудных и |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
соответственно определяются из выражений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
I |
|
|
( y) |
|
U |
2 |
|
|
|
|
|
y |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
U |
х.х. |
(y) |
U |
2 |
cos(2 |
|
) |
|
|
|
|
|
х.х. |
|
|
|
Zв |
sin(2 |
|
|
) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||
54
В эти выражения переменная времени не входит, следовательно, распределение действующих значений напряжения и тока вдоль линии с течением времени не меняется. Рассмотренный режим колебаний называют режимом стоячих волн.
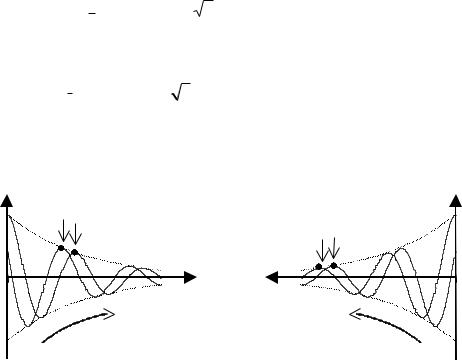
На рисунках 9.1.а) показано распределение действующих значений напряжения и тока вдоль линии. В линии имеются точки, где амплитуда колебаний равна нулю (узлы напряжения или тока) и точки, где амплитуда колебаний максимальна (пучности напряжения или тока). Стоячие волны являются результатом сложения падающей и отражённой волн с равными амплитудами. В пучностях фазы обеих волн совпадают и амплитуда суммарной волны вдвое больше амплитуды падающей волны, а в узлах фазы противоположны и амплитуда суммарной волны равна нулю.
Входное сопротивление разомкнутой линии (в режиме холостого хода) на расстоянии у определяется как:
|
U 2 cos(2 |
y |
|
|
|
|
|
|
|
|
|
|||||
|
|
) |
|
|
|
|
y |
|
|
|
|
|||||
Z вх(х.х.) ( y) |
|
|
j Z |
в |
ctg(2 |
) |
j X |
вх(х.х.) |
( y). |
|||||||
j |
U |
2 |
sin(2 |
|
y |
) |
|
|||||||||
|
Z |
|
|
|
|
|
|
|
|
|
|
|
||||
|
в |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, входное сопротивление линии в таком режиме будет реактивным.
|
X вх(х.х.)(y) |
График зависимости |
представлен на рисунке 9.1.б). Разомкнутая на конце |
линия длиной от 0 |
до /4 имеет входное сопротивление емкостного характера ( |
X вх(х.х.) 0
). Линия длиной /4 имеет входное сопротивление равное 0, т. е. такой отрезок длинной линии аналогичен последовательному колебательному контуру без
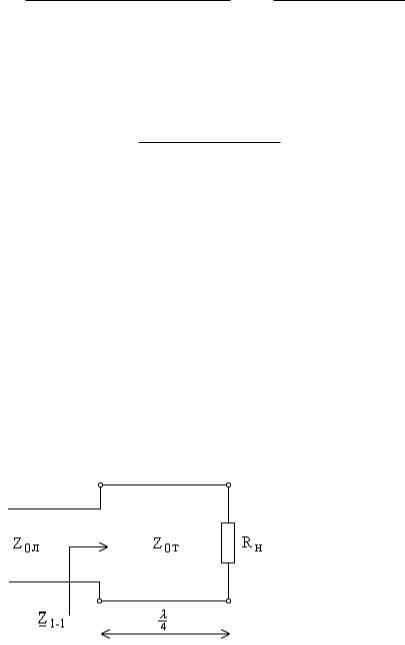
Xвх(х.х.) 0 |
|
|
|
потерь ( |
). Линия |
длиной от /4 |
до /2 имеет входное сопротивление |
|
X вх(х.х.) 0 |
|
|
индуктивного характера ( |
). Линия длиной /2 имеет бесконечное входное |
||
|
X вх(х.х.) |
|
|
сопротивление |
( |
), т. е. такой |
отрезок длинной линии аналогичен |
параллельному колебательному контуру без потерь. В режиме короткого замыкания, т. е.
55

когда линия на конце замкнута |
(Z н 0) |
, графики распределения амплитудных значений |
напряжения и тока, вдоль линии показаны на рисунках 9.2.а.
Рис. 9.2 В короткозамкнутой линии, также как и в разомкнутой, имеет место режим стоячих
волн. При нагрузке линии на реактивное сопротивление |
(Zн j Xн ) |
образуются |
стоячие волны, как и в режимах холостого хода и короткого замыкания. Реактивный элемент, подключаемый к линии в качестве нагрузки, можно заменить эквивалентным отрезком линии, входное сопротивление которого равно сопротивлению реактивного элемента. Емкостной элемент можно заменить разомкнутым отрезком линии длиной
|
|
|
|
4 |
4 |
||
|
, а индуктивный элемент – короткозамкнутым отрезком длиной |
|
. При этом, |
если нагрузка индуктивная, узлы и пучности сдвигаются влево, в сторону генератора, и вправо, в сторону нагрузки, если она емкостная.
Если линия нагружена на резистивное сопротивление, равное волновому
(Zн R н Zв )
, то нагрузка является согласованной. В этом случае комплексные действующие значения напряжения и тока на выходных зажимах линии связаны
U 2 I 2 Z н I 2 Zв соотношением: .
56
Напряжение и ток совпадают по фазе, так как в линии без потерь |
|
Zв |
||||
|
|
|
принимает |
|||
|
|
0 |
||||
действительное (не комплексное) значение. Коэффициент отражения |
|
|
|
, и в линии |
||
существует только падающая волна с неизменной амплитудой. |
|
|
|
|
||
9.1. Линии без искажений и использование отрезков длинных линий |
||||||
При подключении несогласованной резистивной нагрузки |
|
(Z н Rн Zв) |
||||
|
|
|
|
|||
действующие значения |
напряжения и тока на выходных зажимах |
|
линии связаны |
|||
U 2 I 2 |
Z н I 2 R |
н |
|
|
|
1 |
|
|
|||||
соотношением: |
|
, тогда коэффициент отражения |
|
|
|
. В линии |
одновременно присутствуют как бегущие, так и стоячие волны. Такой режим называется режимом смешанных волн. В этом режиме энергия волны частично поглощается нагрузкой, а частично отражается к источнику сигнала, т.е. к входу линии.
Чем больше отличие между значениями сопротивления нагрузки |
Rн |
|||
и волновым |
||||
сопротивлением |
Zв |
|
отличие между максимальным |
и минимальным |
, тем больше |
||||
|
Umax |
Umin |
|
|
значениями напряжения |
и |
. Минимальное значение напряжения определяет |
||
уровень бегущей волны. Для количественной оценки отличия напряжений в минимуме и максимуме, т.е. степени рассогласования линии с нагрузкой, служит коэффициент бегущей волны:
Kбв Umin 1
Umax 1
Кбв характеризует величину бегучей волны и изменяется от нуля до единицы. Режим бегущей волны (желательный режим для линий передачи сигнала) будет при
значении Кбв = 1, а при Кбв = 0 будет режим стоячих волн.
Иногда используют понятие коэффициента стоячей волны, который определяют как:
K |
св |
|
1 |
|
|
|
Kбв |
Kсв |
|||||
|
|
|||||
|
|
|
||||
|
|
|
|
. Очевидно, |
может изменяться от единицы до бесконечности. |
|
57
Входное сопротивление линии без потерь будет
Zвх ( y) Z |
|
Z н cos( |
y) |
j |
Zв |
sin( |
y) |
Z |
|
Z |
н |
j Zв |
tg( y) |
|
|
в |
|
cos( |
y) |
j |
Z н |
sin( |
y) |
в |
|
|
j Zн tg( y) |
. |
|||
|
Zв |
|
Zв |
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С учётом |
|
|
окончательно находим |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Z н j Zв tg( |
2 |
|
y) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Z вх ( y) Zв |
|
|
2 |
|
. |
|
|
|
||||
|
|
|
|
|
|
Zв j Z н tg( |
|
|
y) |
|
|
|
|
||
(9.2)
В реальных линиях часть полезной мощности теряется в виде тепловых потерь. Чтобы передача энергии осуществлялась с наименьшими потерями, фидер должен работать в режиме бегущих волн. Кроме того, наличие отражённой волны приводит к неравномерному распределению действующих значений напряжения вдоль линии и, следовательно, увеличивает потери на излучение и опасность электрического пробоя линии в точках, где действующие значения напряжения достигают наибольших значений. Для того чтобы фидер работал в режиме бегущих волн, его нагрузочное сопротивление должно быть равно волновому. Рассмотрим согласование линии с нагрузочным сопротивлением, не равным волновому, с помощью четвертьволнового трансформатора. Схема такого согласования приведена на рис. 26.1.
Рис. 9.3
Z |
0 л |
Пусть волновое сопротивление линии равно |
, а сопротивление нагрузки резистивное, |
Zн Rн |
Z |
0 л |
|
причём |
|
. Расчёт четвертьволнового трансформатора сводится к |
|
определению его волнового сопротивления |
Z0т |
||
, которое должно быть выбрано так, |
|||
58

чтобы входное сопротивление трансформирующего отрезка с нагрузкой |
R н |
|
||||||||||||||||
было бы |
||||||||||||||||||
|
|
|
|
|
|
|
|
Z1 1 Z0 л |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
||||||
равно волновому сопротивлению линии: |
|
|
|
|
. Подставим в формулу (9.2) |
. В |
||||||||||||
результате находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rн j Z0т tg( |
2 |
|
|
|
Z02т |
|
|
|
|
||||||
Z 1 1 Z |
|
|
4 ) |
|
|
Z |
0 л |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
0 |
т Z |
|
j R |
|
|
tg( |
2 |
|
) |
|
Rн |
|
|
||||
|
т |
н |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
0 |
|
|
|
4 |
|
|
|
|
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z0т |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Rн Z0л |
|
|
|
|
|
|
|
|
|
|
|
||||||
откуда получим |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z0т |
|
|
|
|
|
|
|
|
|
|
|
Подбор необходимой величины |
для линии осуществляется путём изменения |
|||||||||||||||||
расстояния между проводами. Таким образом, четвертьволновый согласующий трансформатор позволяет устранить отражённую волну в основной части линии при произвольной нагрузке. Однако на практике рассмотренный способ согласования иногда применять нецелесообразно, так как в конструктивном отношении неудобно иметь согласующие трансформаторы с очень большими или, наоборот, очень малыми волновыми сопротивлениями.
Более совершенным с практической точки зрения оказывается метод согласования, предложенный В.В.Татариновым. Сущность этого метода состоит в следующем. Пусть
|
|
Y |
л |
|
1 |
|
|
|
Z0 л |
||||
|
|
0 |
|
|||
линия с волновой проводимостью |
|
|
|
подключена к нагрузке, имеющей |
||
Y н |
1 |
gн j bн |
|
|
|
|
Z н |
|
|
|
|
||
проводимость |
|
. Поскольку входная проводимость линии являются |
||||
Y вх(y) Z вх1(y) gвх ( y) j bвх (y)
функциями её длины, то |
. Допустим, на некотором |
|
|
0 |
|
расстоянии |
от конца линии (в сечении 1-1), как это показано на рис. 9.3, резистивная |
|
59
|
|
g |
вх |
(l 0 ) Y |
л |
|
|
|
0 |
||
составляющая входной проводимости равна волновой проводимости линии: |
|
|
, |
||
b |
вх |
( 0 ) |
|
|
|
а реактивная составляющая принимает какое-то значение |
. Если теперь между |
|
|||
|
|
||||
|
|
bш bвх (l 0 ) |
|
|
|
точками 1-1 в цепь включить элемент с реактивной проводимостью |
|
, то |
|
||
Y эк (l 0 ) Y0 j (bвх bш) Y0 |
|
||||
эквивалентная входная проводимость будет равна |
|
|
|
. |
|
Следовательно, в основной части линии, слева от сечения 1-1, будет существовать только падающая волна.
Рис. 9.4
|
bш bвх(l 0 ) |
В качестве элемента с реактивной проводимостью |
удобно |
использовать так называемый параллельный реактивный шлейф – отрезок линии, короткозамкнутый на конце. Волновое сопротивление короткозамкнутого шлейфа обычно
выбирают равным |
Z0л |
ш |
, а его длина |
определяется из условия равенства |
проводимостей. Так как входная проводимость короткозамкнутого отрезка линии без учёта
Y |
ш |
(l |
ш |
) j Y0 |
ctg( l |
ш |
) |
j |
b (l 0 ) |
|
|
|
|
|
|
вх |
|||
потерь |
|
|
|
|
|
|
|
|
, то для выполнения этого условия |
необходимо, чтобы
l ш 1 arcctg bвхY(0l 0)
.
60
61
