Лекции 4 семестра по направлению 210700

Тема 1. Спектральное представление колебаний

Лекция 1 Спектральное представление негармонических периодических сигналов

В основе расчетов электрических цепей при периодических несинусоидальных или непериодических воздействиях лежат спектральные представления токов и напряжений. Спектр является важнейшей и единственной формой аналитического описания сигналов в рамках линейной теории. Основная идея использования такого метода исследований заключается в том, что воздействие представляется в виде суммы простых функций, например, гармонических. Тогда, используя линейность оператора электрической цепи, можно свести задачу преобразования цепью этого воздействия к задаче преобразования элементарных функций, что, безусловно, проще.

Для представления периодических негармонических сигналов, т.е. сигналов, отличающихся от гармонических колебаний, для которых справедливо соотношение:

s(t) {u(t);i(t)}

Причем s(t) обозначает либо напряжение, либо ток, т.е. В этом случае ряд Фурье имеет следующий вид:

1

Таким образом, периодический сигнал в форме ряда Фурье представляет собой

кратными частоте 1.

Выражения (1.2) и (1.3) являются формулами разложения, а выражение (1.1) – формула обращения. Такое название объясняется тем, что совокупность коэффициентов С(k) является спектром сигнала

Используя формулу Эйлера

e jk 1t cosk 1t j sin k 1t,

(1.4)

можно записать ряд Фурье в комплексной форме:

s(t) C( jk)exp( jk 1t);

k

(1.5)

T / 2

. (1.6)

Причем из сравнения с формулой (15.1) следует

;

В комплексной форме ряда Фурье присутствуют положительные и отрицательные частоты. Однако реально существуют лишь положительные частоты, а отрицательные это математическая абстракция – следствие использования комплексных экспоненциальных

Тогда можно из формулы (1.5) получить:

s(t) C(0) 2 C( jk ) cos k 1t (k)

k 1

2

- фаза гармоники.

Это третья форма ряда Фурье в виде суммы реальных гармоник.

Таким образом, любая спектральная составляющая характеризуется амплитудой и фазой. Спектром амплитуд (амплитудным спектром) называется зависимость амплитуд гармоник от частоты. Зависимость начальных фаз гармоник от частоты называется спектром фаз (фазовым спектром). Спектр амплитуд и спектр фаз, представленные в графическом виде, называются спектральными диаграммами.

Активная мощность периодического негармонического сигнала равна сумме мощностей всех составляющих его обобщенного спектра:

спектр сигнала. Мощность гармонических функций равна ½. Формула (1.9) носит название равенства Парсеваля.

Для ряда Фурье в комплексной форме, получим равенство Парсеваля в следующем

виде:

При ограничении спектра по частоте мощность сигнала уменьшается, т.е. равенство Парсеваля позволяет судить о потерях мощности при той или иной фильтрации сигнала.

Рассмотрим пример расчета амплитудного спектра периодического сигнала

Рис. 1.1

3

Определим спектр такого сигнала из формулы (16). Используя формулу Эйлера (1.4), далее

31, 61, 91

и т.д., будут равны нулю. Полученная формула позволяет вычислить амплитудный спектр комплексного ряда Фурье, т.е. включает гармоники с положительными и отрицательными частотами. Чтобы вычислить амплитудный спектр одностороннего ряда Фурье (включает реальные гармоники с положительными частотами), амплитуды гармонических составляющих необходимо умножить на 2. Тогда получим: U0 =U(0)=U/3,

Um (1) 0,551U , Um (21) 0,276U, Um (41) 0,138U, Um (51) 0,11U

и т.д. Амплитудный спектр заданного периодического сигнала приведен на рис. 1.2.

Рис. 1.2

Лекция Спектральное представление непериодических сигналов

Спектральный анализ периодических сигналов с помощью ряда Фурье может быть обобщен на случай непериодических сигналов. Среди непериодических сигналов наибольшее использование находят финитные сигналы, т.е. сигналы, ограниченные по длительности, например, от 0 до t1 (см. рис. 2.1,а).

ограниченной энергией. Если дополнить финитный сигнал, т.е. сигнал, ограниченный по длительности, таким же, но следующим через интервал, равный n T (T-период), то получим рассмотренный выше периодический сигнал (см. рис. 2.1,б).

4

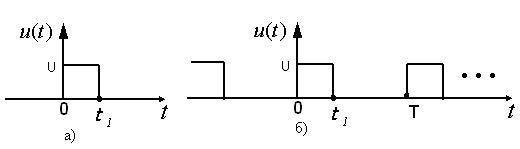
Рис. 2.1 Очевидно, исходный финитный сигнал отличается от периодического сигнала лишь

тем, что у него период стремится к . Тогда получим:

- это обратное преобразование Фурье.

Таким образом, непериодический сигнал и его спектральная плотность связаны взаимнооднозначным прямым и обратным преобразованиями Фурье.

5

Из сравнения прямого преобразования Фурье с рядом Фурье видно, что и там, и там сигнал представляется в виде суммы гармоник, но в отличие от ряда Фурье здесь сумма

ампл

Гц

спектральная плотность имеет смысл плотности амплитуды спектра и измеряется

. Таким образом, спектральная плотность показывает распределение амплитуд по частоте. Другой важный вывод: спектральная плотность непериодического сигнала и огибающая спектра периодического сигнала, полученного из непериодического путем его повторения

через период T , совпадают по форме и отличаются только масштабом. Это позволяет вычислять спектр периодического сигнала, рассчитывая его огибающую с помощью прямого преобразования Фурье, что гораздо легче, чем вычисление коэффициентов ряда Фурье.

Так как интегрирование – линейная операция, то преобразования Фурье обладают свойствами линейности (это линейный функциональный оператор). Введем обозначение:

F( )-прямое преобразование Фурье; F-1( )-обратное преобразование Фурье.

Рассмотрим основные свойства преобразования Фурье, которые формулируются как теоремы.

6

Интегралы в этих выражениях называются свертками.

Теорема о масштабе (подобии).

Если известен сигнал и его спектральная плотность, то Фурье-преобразование равно

F s(kt) 1k S( j k )

, где k – коэффициент.

Теорема о модуляции.

Теорема Парсеваля.

7