Sbornik_ispr

Аналогично определяются c132 =20; c133=20.

Так как все пути имеют одинаковую емкость, выбирается первый путь.

4.Из емкости ребер u12 и u23 вычитается v13 и оставшиеся емкости ребер заносятся в таблицу 5.1. Так как v13 с131, то на этом распределение требований v13 заканчивается.

Итерация 2.

5. Из матрицы требований V= ║vst║ из оставшихся требований выбирается пара вершин с максимальным значением vst . Это - пара вершин 3

– 6, для которых

v36 = 16.

6. Из схемы графа рис.5.1 находятся кратчайшие пути по числу ребер

между вершинами 3 и 6

емкости ребер заносятся в таблицу 5.1. Так как v36 с362 , то на этом распределение требований заканчивается.

Итерация 3.

9. Из матрицы оставшихся требований выбирается пара вершин с максимальным значением vst . Это пара вершин 5 – 6, для которых v56 = 16.

41

10. Из схемы графа рис. 5.1 находятся кратчайшие пути по числу ребер между вершинами 5 и 6

12. После распределения требований v56 по всем путям осталось v56 = 8

не распределенных каналов.

Итерация 4.

13.Из матрицы требований выбирается последнее требование v24 = 12.

14.Из схемы графа рис.5.1 находятся кратчайшие пути

16. Так как ни в одном из путей нет свободных каналов, то остаются

нераспределенными v24 = 12 каналов.

Так как на сети остается большой резерв каналов, то, вероятнее всего,

принята не оптимальная процедура поиска ПРК. На итерации 1 из трех возможных путей был выбран первый путь. Все итерации следует повторить при выборе на первой итерации второго пути, а затем третьего. Фактически,

последовательный алгоритм может привести к полному перебору. Поэтому используется приближенный параллельный алгоритм, либо для поиска

оптимального решения используется метод линейного программирования.

В таблице 5.2 приведены результаты распределения каналов последовательным алгоритмом для случая, когда на итерации 1 выбирается

ПРК, чем в первом, хотя он, как и полученный в цикле 1, не является

допустимым.

Таблица 5.1

Результаты нахождения ПРК последовательным алгоритмом

(цикл 1)

43

ПРК не допустим, т.к. не распределено 20 каналов.

Таблица 5.2

Результаты нахождения ПРК последовательным алгоритмом (цикл 2)

44

ПРК не допустим, т.к. не распределено 12 каналов.

Параллельный алгоритм нахождения ПРК

Поясним параллельный алгоритм на рассмотренном выше примере

(рис.5.1).

Параллельный алгоритм нахождения ПРК состоит в следующем.

1.Из матрицы V выбирается требование V13=18 каналов.

2.Из схемы графа рис.5.1 определяются кратчайшие пути (по числу ребер).

1,2,31, 1,5.32, 1,4,33 .

3. Распределяются 18 каналов равномерно на три пути

с1(1,3)= с2(1,3)= с3(1,3)=6 каналов.

4.Повторяются пункты 1-3 для других потоков, не обращая внимания на емкости ребер.

с3(5,6) = с4(5,6)=4.

5.Составляется матрица задействованных емкостей ребер кратчайших путей для идеального ПРК (без учета заданных емкостей ребер) (таблица 5.3).

45

с2(5, 6).

8.Выбирается с1(1,3) и проверяется, есть ли кратчайший путь,

соответствующий данной паре вершин и состоящий из ненасыщенных ребер. Если есть, то переходят к пункту 9, если нет, то к пункту 11.

9.Между парой 1-3 есть ненасыщенный путь с числом каналов с2(1, 3).

Величина перераспределяемой емкости равна 2 (см. ребро 23).

Рассчитывается с2ij. Т.к. ПРК недопустим, то переходим к п. 10.

10.Повторяем пункты 7, 8 и 9 для ребра 34. По таблице 5.3 определяем,

что перегруженному ребру 34 соответствуют пути с числом каналов с3(1, 3); с2(2, 4); с2(3, 6); с4(5, 6). Ищем путь с ненасыщенными ребрами. Находим для пары 1-3 путь с2(1, 3), который проходит по ненасыщенным ребрам 15 и 35. Рассчитываем с3ij . Полученные элементы с3ij определяют искомый ПРК.

11.Если кратчайшие пути с ненасыщенными ребрами для данной пары вершин не найдены, то переходим к следующему пути. Процесс повторяется до тех пор, пока не будет найден ненасыщенный путь.

Если такого пути не существует, то требования не могут быть удовлетворены полностью.

Как видно из рассмотренного примера, параллельный алгоритм по сравнению с последовательным позволил получить лучший ПРК. Однако параллельный алгоритм как и последовательный также является

46

с1(3,6) = 8

3-6

8 8

47

4.Варианты заданий

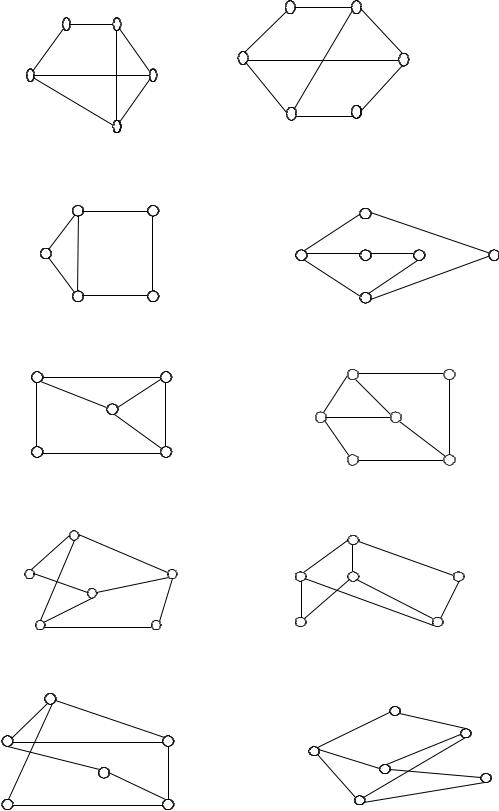
1.Структура первичной сети определена графами на рис. 5. 2 и 5. 3.

2.Матрица требований, ненулевые элементы которой указаны в таблице 5.4

для графов, структура которых приведена для вариантов 1 – 10, и в таблице 5.5

для графов, структура которых приведена для вариантов с 11 по 20. Емкости ребер в числе стандартных каналов заданы весами ребер на графах.

3. Максимальный ранг пути rmax=3.

48

Таблица 5.4

Исходные данные для вариантов с первого по десятый.

4.Содержание отчета

1.Вариант задания: граф сети, матрица требований, матрица емкостей.

2.Решение задачи нахождения ПРК последовательным алгоритмом.

3.Решение задачи нахождения ПРК параллельным алгоритмом.

4.Сравнение полученных результатов.

Литература

1.Глушков В.М., Калиниченко Л..А., Лазарев В.Г., Сифоров В.И., Сети ЭВМ – М.: Связь, 1977.- С. 136-149.

2.Сборник описаний лабораторных работ по курсу “Проектирование и техническая эксплуатация сетей электросвязи”. – М. 1990.

49

Рис.5.2. Структуры графов для вариантов с 1 по 10

50