Sbornik_ispr

План УМД на 2010/2011 уч. год

Сборник методических указаний для проведения лабораторно-практических занятий по дисциплине

СЕТИ СВЯЗИ

Составитель: А.П.Пшеничников, канд. техн. наук, профессор

Издание утверждено Советом факультета С и СС. Протокол № 9 от 24.05.2011г.

Рецензент Ц.Ц. Михайлова, канд. техн. наук, доцент

2

Тема 1

Структурные матрицы сетей и операции с ними

1. Цель работы

Изучить и практически освоить описание структурных параметров сетей связи с использованием математического аппарата булевой алгебры. Путем преобразования структурных матриц получить перечень путей, сечений и квазисечений.

2.Задание

2.1.Ознакомиться по [1] с основными определениями структурного анализа сетей связи: граф сети, путь, ранг пути, способы записи путей, сечение,

квазисечение, правила булевой алгебры.

2.2.Изучить методы получения множества путей и сечений из структурной матрицы.

2.3.Получить задание у преподавателя. Варианты заданий приведены на рис.

1.4, 1.5 и в таблицах 1.1, 1.2.

2.4.Согласно полученному варианту задания провести анализ сети:

записать структурную матрицу сети;

визуально по схеме графа найти и записать все возможные пути от узла i к узлу j; номера узлов i и j взять из таблиц 1.1 и 1.2 в соответствии с номером варианта задания;

определить пути ранга r 3 для заданной пары узлов;

путем преобразования структурной матрицы найти и записать все пути

от узла i к узлу j и все пути ранга r 3;

по структурной матрице построить дерево путей с корнем в узле i ранга r 3 для связи с узлом j и сравнить полученный результат с результатами, полученными при выполнении предыдущих пунктов;

3

используя аппарат булевой алгебры, найти квазисечения между узлами i

и j для множества путей с рангом r 3.

3. Теоретическая часть

Структура сети (ее топология) - это совокупность связей между элементами сети, отражающая их взаимодействие.

Для изучения структурных свойств сети ее представляют в виде графа

G ={A,B}.

Граф задается множеством вершин А = {a1,a2,…, ai ,…, an} и

множеством ребер

В = { bij }, соединяющих вершины графа, i,j =1,n, где n – число вершин графа.

Таким образом, станциям и узлам сети ставятся в соответствие вершины, а

линиям передачи – ребра. Ребру может быть приписан вес или совокупность весов, характеризующих его свойства, например, длина в километрах,

пропускная способность в числе каналов и т.п. Так как каналы могут быть одностороннего и двустороннего занятия, то и соответствующие им ребра будут направленными (ориентированными) и ненаправленными

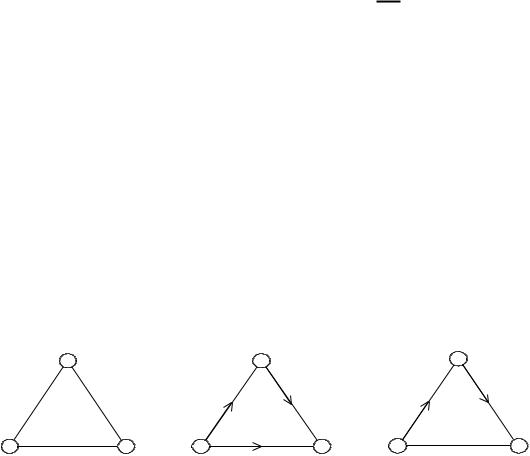
(неориентированными). На рис. 1.1 приведены примеры ориентированных и неориентированных графов.

ребру, а ребро – инцидентным этим вершинам. Аналогично два разных ребра называются смежными, если они имеют общую вершину. Число ребер,

инцидентных данной вершине, называются рангом (степенью) вершины.

Вершина ранга 1 называется оконечной (тупиковой, висячей). Вершина ранга 0

называется изолированной.

Путь st из вершины аs в вершину аt - это упорядоченная

последовательность ребер, начинающаяся в аs, заканчивающаяся в аt и не проходящая дважды через одну и ту же вершину, причем в промежуточной

вершине конец предыдущего ребра совпадает с началом последующего

(условие непрерывности каналов в сети). Обычно путь записывается перечнем

Минимальный ранг пути равен 1, максимальный – n-1, когда путь проходит через все вершины, где n – число вершин графа.

Все пути от аs к аt образуют множество путей mst , а совокупность двух множеств, соответствующих противоположным направлениям, - множество всех путей между аs и аt st = mst mts. Для ненаправленных графов Мst

= mst = mts.

Связным называется такой граф, любые две вершины которого связаны хотя бы одним путем. Граф называется h – связным, если любые две вершины связаны независимыми путями, число которых не менее h. Независимыми

называются такие пути, которые не включают одни и те же ребра (независимые по ребрам) или одни и те же вершины (независимые по вершинам). Часто понятие связности относят к заданным вершинам аs и аt (hst - связность).

Сечением графа называется совокупность ребер, которые надо изъять,

чтобы нарушилась его связность. Сечением st по отношению к вершинам аs

5

и аt называются такие сечения, при которых вершины аs и аt оказываются в разных подграфах. Рангом сечения вершины i r( i) называется число входящих в него ребер. Подграфом графа G = {A,B} называют граф, все вершины которого принадлежат множеству А, а все ребра – множеству В.

Квазисечением называют сечение, рассекающее пути только до

определенного ранга.

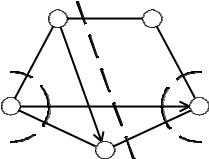
Проиллюстрируем приведенные определения на примере. Граф на рис. 1.2

содержит 5 вершин и 7 ребер. Ранг вершины (число ребер, опирающихся на

данную вершину) для приведенного примера - не более трех.

Рис. 1.2. Сечения графа

Путь записывается перечнем ребер, при этом условленно, что если ребро в данном пути направлено от вершины с меньшим индексом к вершине с

6

Множество путей от вершины i =1 к вершине j = 4 можно записать следующим образом:

Для анализа сети, т.е. нахождения путей и сечений, используют

структурную матрицу В. В – квадратная матрица, строки и столбцы которой сопоставлены с вершинами сети. Связь внутри вершины (для i = j)

отображается единицей. Если связи между вершинами нет, то элемент матрицы равен 0. Для сети рис. 1.2 имеем:

7

Элементы матрицы могут рассматриваться как булевы переменные с двумя значениями: 1 – соединение есть, 0 – соединение отсутствует. Поэтому матрицу

В преобразуют как булеву, применяя к ней аппарат булевой алгебры, используя три операции: логическое произведение (конъюнкция), которое обозначается точкой (при записи обычно опускается), логическое сложение (дизъюнкция),

для которой применяется символ , инверсия (черта над переменной или

функцией).

В булевой алгебре 1 1 = 1, а отсюда следуют следующие

преобразования (правила):

a (b c) = (a b) (a c).

8

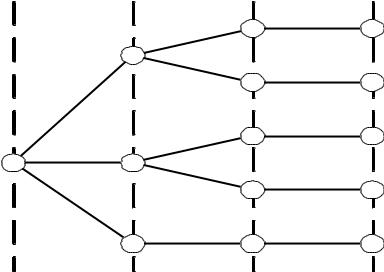
Графический эквивалент перечня путей – дерево путей – можно построить непосредственно по матрице В. Для построения дерева путей из вершины 1

берем первую строку матрицы В и помечаем на графе вершины путей с r =1,

имеющие bij 0. После того, как процесс для строки закончен и отмечены номера вершин (по номеру столбца), переходим к строке одного из тех узлов,

которые расположены на линии r = 1, и продолжаем процесс аналогичным образом. При этом следует учитывать, что вершины в одном пути не должны повторяться. Дерево путей для вершины 1 показано на рис. 1.3.

Для нахождения сечений (или квазисечений, т.е. сечений, рассекающих пути только до определенного ранга) следует заменить функцию m14 на двойственную, заменив дизъюнкцию конъюнкцией и, наоборот, – конъюнкцию дизъюнкцией.

При перемножении булевых многочленов удобно пользоваться формулой (a x) (a y) = a x y. Затем провести упрощение и привести выражение к дизъюнктивной нормальной форме путем исключения лишних членов, пользуясь формулой a ab = a. Каждое слагаемое и есть искомое сечение.

Рис. 1.3. Дерево путей для вершины 1

10