Sbornik_ispr

Продолжение таблицы 3.2

31

Тема 4

Алгоритм поиска маршрутов при динамической маршрутизации вызовов (метод рельефов)

1. Цель работы

Изучить назначение, структуру системы динамического управления потоками сообщений на сетях связи. Рассмотреть метод рельефов. Получить для заданной сети оптимальный по критерию числа транзитных участков план распределения сообщений (ПРС).

2.Задание

1.Изучить упрощенный алгоритм метода рельефов.

2.Решить задачу нахождения i-рельефа на графе сети рис. 4.2. Рассмотреть метод устранения петель. Составить j-столбец матрицы рельефов и j-

столбец матрицы маршрутов (для установления соединения с узлом i).

Числа i и j взять из таблицы 4.1.

3.Переформировать i-рельеф и внести изменения в матрицу маршрутов при выходе из строя ребра kl . Номер ребра kl взять из таблицы 4.1 в

соответствии с выполняемым вариантом.

3.Теоретическая часть

Основой для любого метода динамического управления потоками сообщений является матрица маршрутов (ММ). ММ – это таблица,

содержащая число строк по числу исходящих из рассматриваемого узла ребер и число столбцов по числу узлов сети. Элементами матрицы являются числа,

показывающие порядок выбора ребер, исходящих из данного узла, при установлении соединения с любым другим узлом сети.

Планом распределения сообщений (ПРС) называется совокупность матриц маршрутов всех узлов сети. Если ПРС неизменен за все время работы сети, то на сети имеет место статическое распределение сообщений. Если ПРС может

32

изменяться в зависимости от ситуации, сложившейся на сети (выход из стоя ребер, перегрузка ребер и узлов при случайных колебаниях нагрузки), то на сети имеет место динамическое управление потоками сообщений.

Имеются различные методы, позволяющие изменять матрицы маршрутов в зависимости от ситуации на сети.

Одним из распространенных методов является метод рельефов, в

котором критерием оценки порядка выбора пути является число транзитных участков пути. Наилучшим считается путь, содержащий минимальное число транзитных участков.

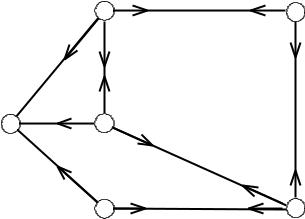
Прежде чем описывать формальный алгоритм, рассмотрим идею метода рельефов на простейшем примере рис. 4.1. Рассмотрим построение рельефа к узлу 1.

Рис. 4.1. Пример структуры сети связи

Строится рельеф к узлу 1 следующим образом. От смежных с узлом 1

узлов 2, 6 и 5 на каждом ребре, соединяющим эти узлы с узлом 1, ставится стрелка в направлении к узлу 1. Цифра 1 у стрелки показывает вес ребра. Веса ребер, равные 1, указывают на то, что при установлении соединения от узлов 2, 6 и 5 к узлу 1 используются пути в один транзитный участок.

33

Путь от узла 3 к узлу 1 через узел коммутации 2 (УК2 ) будет содержать 2

транзитных участка, поэтому стрелка от УК3 к УК2 имеет вес 2 и т.д.

Из узла 6 в направлении к узлу 1 выходят три ребра, веса которых 1, 2 и 3.

Высотой узла 6 по отношению к узлу 1 называется минимальный вес всех исходящих стрелок из узла 6 в направлении к узлу 1. В рассматриваемом случае высота узла 6 по отношению к узлу 1 равна 1.

Рельеф используется при установлении соединения от любого узла сети к узлу 1 для выбора пути с минимальным числом транзитных (коммутируемых)

участков.

Матрица рельефов (высот) обозначает число транзитных участков в кратчайших путях от УКj к УК1. Например, от УК4 столбец матрицы рельефов запишется следующим образом:

1 …

43 3

R4 = 46 2

45 2

Числа в матрице маршрутов задают порядок выбора путей

1 …

43 3

M4 = 46 1 (2)

452 (1)

Врассматриваемом примере пути, начинающиеся с ребер 46 и 45 с точки зрения числа транзитных участков до УК1 равнозначны, поэтому в скобках в

М4 указан другой возможный порядок выбора.

34

При выходе из строя какого-либо ребра сети необходимо произвести перестроение рельефа (лучше всего это сделать на новом чертеже графа сети),

затем сформировать для этого случая столбцы матриц рельефов и маршрутов.

Идея алгоритма заключается в следующем: УК1 посылает в смежные узлы цифру 1. Смежные узлы рассылают цифру 2, смежные смежным – цифру 3

и т.д.

При этом должны соблюдаться следующие три правила.

Правило 1. Если в УКi поступили одинаковые цифры с двух и более направлений, то данный УКi инициирует передачу цифры на 1 больше поступившей по всем без исключения исходящим направлениям. На примере рис. 4.1 это УК4 . К нему поступила цифра 2 от УК6 и УК5 .

Правило 2. Если в УКi поступает цифра только с одного направления, то

УКi передает цифру на 1 больше поступившей по всем направлениям, кроме

того, по которому поступила цифра. По данному направлению будет передана цифра лишь при поступлении в данный УК следующей цифры, т.е. второй по порядку. В примере в УК3 цифра 2 пришла с одного направления – от УК2 и

поэтому в УК2 от УК3 цифра 3 не посылается.

После того, как в УК3 поступит вторая по порядку цифра (в нашем примере 3) от УК3 к УК2 будет послана цифра на 1 большая, т.е. 4.

Правило 3. Инициация передачи цифр по всем направлениям производится на каждом УК только один раз после поступления первой цифры.

35

4. Варианты заданий

Таблица 4.1

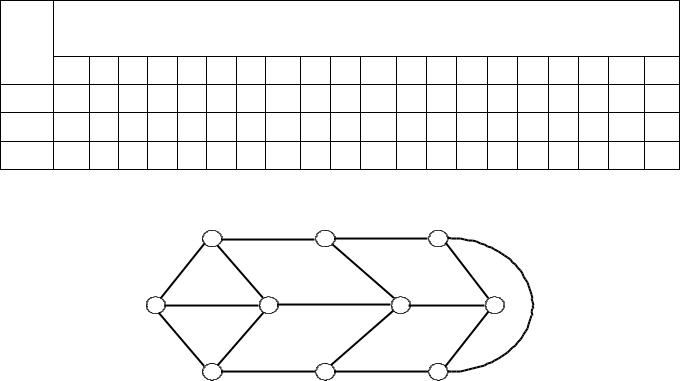
Рис.4.2. Структура сети

4.Содержание отчета

1.Структура сети рис. 4.2 со сформированным i-рельефом.

2.Столбцы матрицы рельефов и матрицы маршрутов для узла j.

3.Структура сети при выходе из строя ребра k,l со сформированным рельефом.

4.Столбцы матрицы рельефов и матрицы маршрутов для узла j при отсутствии ребра k,l .

Литература

1. Сборник описаний лабораторных работ по курсу «Проектирование и

техническая эксплуатация сетей электросвязи». – М.: МТУСИ, 1990.

36

Тема 5

Алгоритмы нахождения плана распределения каналов

1. Цель работы

Освоить постановку задачи нахождения плана распределения каналов

(ПРК) на первичной сети связи. Изучить приближенные последовательный и параллельный алгоритмы нахождения ПРК.

2.Задание

1.Ознакомиться с постановкой задачи анализа и структурного синтеза первичной сети связи.

2.Выполнить нахождение ПРК для заданного варианта сети (рис. 5.2 -

5.3) и заданных в таблицах 5.4 и 5.5 исходных данных последовательным алгоритмом.

3.Выполнить решение задачи параллельным алгоритмом.

4.Сравнить ПРК, полученные разными алгоритмами.

3.Теоретическая часть

Планом распределения каналов (ПРК) называют организацию каналов непосредственно между оконечными узлами и через транзитные узлы в соответствии с имеющейся потребностью в каналах связи.

При построении вторичной сети необходимо определить возможные пути пучков каналов, оценить целесообразность организации пучков каналов по каждому из путей в соответствии с ограниченной емкостью линий связи первичной сети и выбрать емкость путей таким образом, чтобы обеспечить передачу заданных объемов информации.

Для решений задачи нахождения ПРК на первичной сети задаются:

1. Структура первичной сети в виде графа, вершины которого

___

пронумерованы подряд 1, n,___где n – число вершин графа, а ребра задаются парами ij, где i,j = 1, n.

37

2.Емкость каждого ребра в виде матрицы U= ║ uij ║ числа каналов первичной сети.

3.Матрица требований между узлами V= ║vst║, где vst – требуемое число каналов между узлами s и t вторичной сети.

Требуется найти план распределения каналов между заданными парами

узлов с учетом ограниченной емкости ребер первичной сети.

В результате нахождения ПРК решается задача анализа вторичной сети:

можно или нельзя получить допустимый ПРК, т.е. ПРК, удовлетворяющий всем

требованиям матрицы использующий для своей реализации

имеющийся ресурс первичной сети.

Нахождение допустимого ПРК может быть использовано для структурного

синтеза первичной сети, т.е. создания сети с заданными параметрами. При

решении задачи могут учитываться дополнительные ограничивающие условия такие, как условие повышенной надежности, выраженное, например, в

определенном числе независимых путей между узлами, условие, запрещающее образование некоторых путей и др.

В качестве критерия оптимальности можно принять минимальное суммарное число каналов, занятых по всем ребрам первичной сети. При этом для организации оптимального ПРК по сравнению с неоптимальным

сокращается число каналов первичной сети, использованных в путях передачи.

Могут быть и другие критерии оптимальности построения ПРК, например,

суммарная длина всех путей или суммарное число канало-километров.

1. Из матрицы требований V= ║vst║ выбирается пара вершин s и t, между которыми vst >0.

38

2.По графу сети определяется кратчайший путь (пути) stmin . Кратчайший путь находится по числу ребер или по длине пути.

3.С помощью матрицы U= ║uij║ определяется емкость этого пути.

cst = min uij .

ij stmin

uij ребер пути stmin вычитается величина cst . Если vst

то вычисляется разность vst - cst , которая распределяется по следующему пути между вершинами st, если таковой имеется.

5. Выбирается следующая пара вершин и процесс повторяется до тех пор, пока существует хотя бы одно требование vst 0 и, по крайней мере, один путь

stmin между выбранной парой вершин с емкостью

Из описания алгоритма видно, что пучки каналов, которые организуются первыми, имеют преимущества в получении лучших путей по сравнению с последующими. Поэтому последовательный алгоритм не всегда обеспечивает требуемое качество решения.

Пример решения задачи последовательным алгоритмом

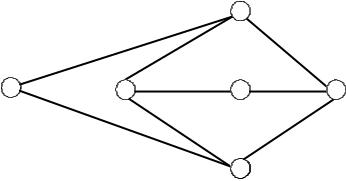
Задана структура первичной сети в виде неориентированного графа

(рис.5.1) и матрица требований V. Число каналов первичной сети задается либо весами ветвей на графе рис.5.1, либо в виде матрицы емкостей ребер U.

4

Рис.5.1. Граф сети

39

Так как граф неориентированный, то в матрицах емкостей ребер и

требований числа каналов можно заполнять только верхнюю половину

матрицы.

Цикл 1.

Итерация 1.

Из матрицы требований V= ║vst║ выбирается пара узлов, между которыми vst имеет максимальное значение. В рассматриваемом примере – это пара вершин 1 – 3, для которых v13 = 18.

2. Из схемы графа рис.5.1 находятся кратчайшие пути по числу ребер

c131= min{ u12 , u23 } = min{ 20 , 20 } = 20;

40