Винеровский процесс

Определение. Гауссовский процесс называется одномерным броуновским движением, или винеровским процессом на интервале 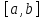, если он обладает следующими свойствами:

1. и функция почти всегда непрерывна

2. Свойство гауссовости приращений: случайная величина 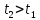, имеет гауссовское распределение с математическим ожиданием 0 и дисперсией , где– положительная константа, то есть:

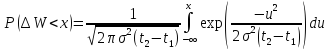
Фрактальное броуновское движение

Классическое броуновское движение, рассмотренное выше, представляет собой хорошую модель марковских случайных фракталов, для которых условная вероятность того, что 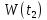достигнет определенного значения при заданном , где, зависит только оти, а не от поведенияпри. Ясно, что существует необходимость введения такого случайного процесса, который обладал бы некоторой памятью. Такой процесс получил названиефрактального броуновского движения (ФБД).

Определение. Гауссовский процесс называется фрактальным броуновским движением с параметром ,, если он обладает следующими свойствами:

1. и функцияпочти всегда непрерывна

2. Свойство гауссовости приращений: случайная величина имеет гауссовское распределение с математическим ожиданием и дисперсией , где,– положительная константа, то есть:

Показатель Херста

Как-то раз гидролог Гарольд Эдвин Херст приехал в Каир в краткосрочную командировку. И остался там почти на 50 лет. Ему надо было решить простенькую статистическую задачку - каких примерно размеров должен быть резервуар, чтобы сглаживать колебания уровня воды в Ниле и не допускать засух. Стандартное решение - посчитать среднее и дисперсию, но по результатам наблюдений получалось, что среднеквадратичное отклонение стремится к бесконечности. То есть приливы-отливы Нила, в отличие от других рек, невозможно предсказать. И все последующие годы Херст путешествовал по Нилу, проводил измерения, пытался найти закономерность. Ему было непросто - компьютеров тогда (20-40-е годы) практически не было. Бросание монетки как способ получить случайную последовательность оказалось слишком трудоемким. Тогда он перенумеровал колоду карт и вытаскивал их, снимая и перемещая по хитрому алгоритму, в зависимости от того, какая цифра выпадет на карте. Так он смоделировал и гауссово распределение, и то, что происходило с уровнем воды. И не только решил задачу, но и стал одним из открывателей новой области математики.

Важнейшим параметром, характеризующим степень самоподобия, является коэффициент H, названный в честь Г. Э. Херста. Показатель Херста (H) может принимать значения 0 ≤ H < 1 (от нуля до единицы), причём:

1. значения в пределах 0 ≤ H < 0,5 (от нуля до половины) принято называть розовым шумом и связывать последний с эргодическим или антиперсистентными свойствами;

2. значение равное H=0,5 принято называть белым шумом, оно означает броуновское движение – наблюдения случайны и некоррелированны, следственно настоящие значения временного ряда не влияют на будущие;

3. значения в пределах 0,5 < H < 1 (от половины до единицы) означают наличие фрактальных свойств временного ряда, следственно указывают на персистентные или трендоустойчивые свойства временного ряда

Расчет коэффициента Херста можно произвести по следующей формуле:

где

H – показатель Херста

N – число периодов наблюдений

S – среднеквадратичное отклонение ряда наблюдений

R – размах накопленного отклонения

a – заданная константа, положительное число (Херст эмпирически рассчитал для краткосрочных временных рядов природных явлений как 0,5)