Диаграмма орбит

Определение. Диаграммой орбит называют график, в котором величины r (В которых функция претерпевает бифуркацию) откладываются по оси ординат, а на каждой горизонтальной прямой y = r наносятся точки притягивающих периодических орбит для x² – x + r, при этом достаточно рассматривать точки в пределах (-2, -0.25).

Для получения притягивающей периодической орбиты для заданного с положим x₀ = 0 (Выбор нуля следует из материала, связанного с множеством Мандельброта). Затем вычисляется орбита с помощью f(x) = x² + r.

На практике достаточно около 200 точек (Но при желании можно взять и несколько десятков тысяч), при этом первые 50 нужно отбросить, а оставшиеся 150 дадут хорошую аппроксимацию периодической орбиты. Для каждого n нанеси точки на график и получить диаграмму орбит.

Обозначим через r₀, r₁, r₂,… точки бифуркации на диаграмме орбит, где итерирование функции заменяет притягивающую орбиту периода 2ⁿ на 2ⁿ⁺¹.

При 0.25 < r < -0.75 существует притягивающая орбита периода 1 При -0.75 < r < -1.25 существует притягивающая орбита периода 2, которая превращается в притягивающую орбиту периода 4, когда c проходит через -1.25 Таким образом r₀ = -0.75, а r₁ = -1.25

Константа Фейгенбаума

Значения точек бифуркации стремятся к пределу r_∞ , называемому точкой Фейгенбаума (Одна из констант Фейгенбаума)

В свою очередь отношение длин последовательных интервалов между точками бифуркации также имеет свой предел.

d - константа Фейгенбаума. Она универсальна, т.к. имеет одно значения для многих различных функций. При этом константа позволяет предсказывать появление хаоса. Интервал между c₀ и с_∞ приблизительно равен

; где ; n=1, 2, 3, … , d ;

Между каждой парой точек r_n и r_n+1 существует точка , которая обладает сверхпртягивающей орбитой с периодом 2n. Для этого значения r, точка x₀ функции f_c удовлетворяет уравнению (x₀) = x₀, а постоянная Фейгенбаума d принимает вид

Значения можно находить численно, используя метод Ньютона для нахождения корней.

Для функции 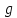(x) = 0 метод будет выглядеть следующим образом (Имея x₀ – нулевое приближение)

При r₀ достаточно близком к корню r, получим, что ,

соответственно

при этом подходящее начальное значение x₀ для можно получить, заменяяd на , где

= , n = 2, 3, …

Проблему для начальных значений при n = 1, 2 , мы решим, полагая

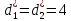
То есть конечный алгоритм применяется к функции =, где– критическая точка. Значениевычисляется итерированием.также вычисляется итерированием. Пусть.

В случае:

• получим

• имеем

Конец итерационному процессу можно выбрать, например, исходя из заданной точности.

<ε

х

Рис. 3 Бифуркационная диаграмма Ферхюльста

Диаграмма орбит показывает периодические орбиты для f_r(x) = rx(1-x). При этом на участке около r ≈ 3.83 диаграмма сильно разрежена, видна белая полоса и орбиты имеют период 3. При этом орбиты должны быть отталкивающими, а период 3 означает наличие орбит с периодами n = 1,2,3,…

Теорема Шарковского.

Пусть I – конечный или бесконечный интервал в R. Предположим, что отображение f : I I непрерывно. Если существует точка периода n, то существуют точки f периода k для каждого целого положительного k, k > n, из следующего списка (Упорядочение Шарковского)

→ 3 → 5 → 7 → 9 → 11 → 13 → …

→ 3*2 → 5*2 → 7*2 → 9*2 → 11*2 → 13*2 → …

→ 3*2² → 5*2² → 7*2² → 9*2² → 11*2² → 13*2² → …

…………………………………

→ 2ⁿ → 2^n-1 → … → 2⁵ → 2⁴ → 2³ → 2² → 2 → 1.

Тройка является частным случаем этой теоремы, причем стоит выделить тот факт, что число различных периодов для орбит f конечно только в том случае, когда периоды выражаются через , для некоторогоn. При орбите нечетного периода, большего единицы, число различных периодов бесконечно.