Производная курсовая

8. Вычислить производную 2-го порядка от неявной функции: .

9. Вычислить производную 2-го порядка от функции, заданной параметрически:

.

10. Вычислить предел с помощью формулы Тейлора: .

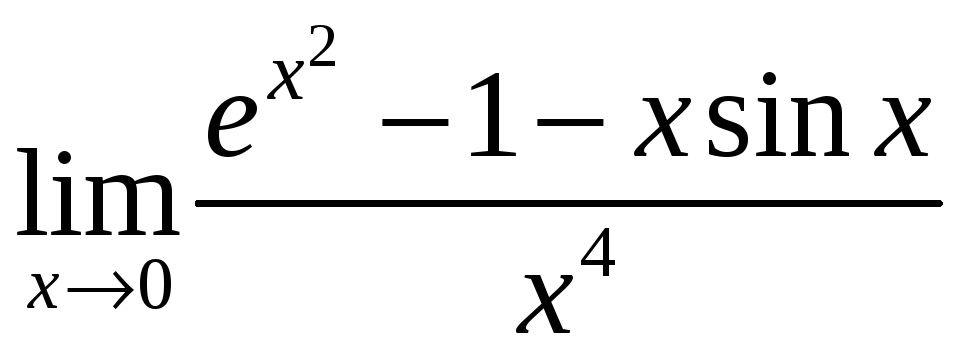11. В какой точке касательная к параболе параллельна хорде, соединяющей

точки и ?

Вариант 23

1. Вычислить пределы с помощью правила Лопиталя:

а) ; б) .

2. Построить графики функций:

а) (а также график производной по графику построенной функции); б) .

3. На правой ветви гиперболы , , найти точку , ближайшую к

прямой .

4. Вычислить функции , используя формулу Лейбница.

5. Оценить с помощью формулы Тейлора абсолютную погрешность

приближенной формулы: .

6. Составить уравнения касательной и нормали к графику функции

, .

7. Составить уравнения касательной и нормали к графику функции

в точке .

8. Вычислить производную 2-го порядка от неявной функции: .

9. Вычислить производную 2-го порядка от функции, заданной параметрически:

.

10. Вычислить предел с помощью формулы Тейлора: .

11. Проверить, что между корнями функции находится корень

ее производной. Пояснить графически.

Вариант 24

1. Вычислить пределы с помощью правила Лопиталя:

а) ; б) .

2. Построить графики функций:

а) (а также график производной по графику построенной функции);

б) .

3. Найти сторону основания и боковое ребро правильной шестиугольной

призмы, вписанной в сферу единичного радиуса и имеющей среди всех

таких призм наибольшую полную поверхность.

4. Вычислить функции , используя формулу Лейбница.

5. Оценить с помощью формулы Тейлора абсолютную погрешность

приближенной формулы: .

6. Составить уравнения касательной и нормали к графику функции ,

.

7. Составить уравнения касательной и нормали к графику функции

в точке .

8. Вычислить производную 2-го порядка от неявной функции: .

9. Вычислить производную 2-го порядка от функции, заданной параметрически:

.

10. Вычислить предел с помощью формулы Тейлора: .

11. Написать формулу Лагранжа для функции и найти на .

Вариант 25

1. Вычислить пределы с помощью правила Лопиталя:

а) 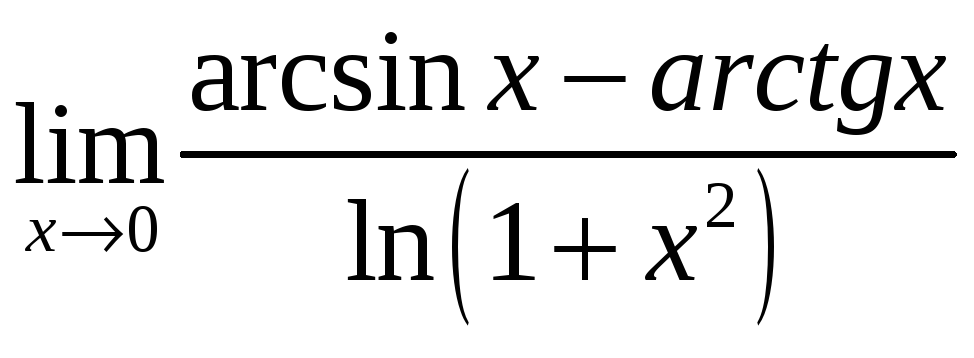; б).

2. Построить графики функций:

а) (а также график производной по графику построенной функции);

б) .

3. Найти радиус основания и высоту прямого кругового цилиндра,

вписанного в сферу единичного радиуса и имеющего среди всех таких

цилиндров наибольший объем.

4. Вычислить функции , используя формулу Лейбница.

5. Оценить с помощью формулы Тейлора абсолютную погрешность

приближенной формулы: , .

6. Составить уравнения касательной и нормали к графику функции

, .

7. Составить уравнения касательной и нормали к графику функции

в точке .

8. Вычислить производную 2-го порядка от неявной функции: .

9. Вычислить производную 2-го порядка от функции, заданной параметрически:

.

10. Вычислить предел с помощью формулы Тейлора: .

11. На кривой найти точку, в которой касательная параллельна хорде, со-

единяющей точки и .

Вариант 26

1. Вычислить пределы с помощью правила Лопиталя:

а) ; б) .

2. Построить графики функций:

а) (а также график производной по графику построенной функции);

б) , .

3. На отрезке прямой между точками и найти такую точку ,

чтобы сумма квадратов расстояний от неё до двух прямых: , и

, была наименьшей.

4. Вычислить функции , используя формулу Лейбница.

5. Оценить с помощью формулы Тейлора абсолютную погрешность

приближенной формулы: .

6. Составить уравнения касательной и нормали к графику функции

, .

7. Составить уравнения касательной и нормали к графику функции

в точке .

8. Вычислить производную 2-го порядка от неявной функции: .

9. Вычислить производную 2-го порядка от функции, заданной параметрически:

.

10. Вычислить предел с помощью формулы Тейлора: .

11. Написать формулу Коши для функций и

, и найти на .

Вариант 27

1. Вычислить пределы с помощью правила Лопиталя:

а) ; б) .

2. Построить графики функций:

а) (а также график производной по графику построенной функции); б) .

3. Найти основание и боковую сторону равнобедренного треугольника,

вписанного в окружность единичного радиуса и имеющего среди всех таких

треугольников наибольший периметр.

4. Вычислить функции , используя формулу Лейбница.

5. Оценить с помощью формулы Тейлора абсолютную погрешность

приближенной формулы: .

6. Составить уравнения касательной и нормали к графику функции

, .

7. Составить уравнения касательной и нормали к графику функции

в точке .

8. Вычислить производную 2-го порядка от неявной функции: .

9. Вычислить производную 2-го порядка от функции, заданной параметрически:

.

10. Вычислить предел с помощью формулы Тейлора: .

11. Написать формулу Лагранжа для функции и найти на .

Вариант 28

1. Вычислить пределы с помощью правила Лопиталя:

а) ; б) .

2. Построить графики функций:

а) (без нахождения точек перегиба, а также график производной по графику построенной функции);

б) .

3. Найти основание и боковую сторону равнобедренного треугольника,

вписанного в окружность единичного радиуса и имеющего среди всех таких

треугольников наибольшую площадь.

4. Вычислить функции , используя формулу Лейбница.

5. Оценить с помощью формулы Тейлора абсолютную погрешность

приближенной формулы: .

6. Составить уравнения касательной и нормали к графику функции ,

.

7. Составить уравнения касательной и нормали к графику функции

в точке .

8. Вычислить производную 2-го порядка от неявной функции: .

9. Вычислить производную 2-го порядка от функции, заданной параметрически:

.

10. Вычислить предел с помощью формулы Тейлора: .

11. Применима ли теорема Роля к функции на отрезке ?

Если да, то найти .

Вариант 29

1. Вычислить пределы с помощью правила Лопиталя:

а) ; б) .

2. Построить графики функций:

а) (без нахождения точек перегиба, а также график производной по графику построенной функции);

б) .

3. На правой ветви квадратичной гиперболы , , найти точку ,

ближайшую к началу координат.

4. Вычислить функции , используя формулу Лейбница.

5. Оценить с помощью формулы Тейлора абсолютную погрешность

приближенной формулы: , .

6. Составить уравнения касательной и нормали к графику функции

, .

7. Составить уравнения касательной и нормали к графику функции

в точке .

8. Вычислить производную 2-го порядка от неявной функции: .

9. Вычислить производную 2-го порядка от функции, заданной параметрически:

.

10. Вычислить предел с помощью формулы Тейлора: .

11. В какой точке касательная к кривой параллельна хорде соединяющей

точки и ?

Вариант 30

1. Вычислить пределы с помощью правила Лопиталя:

а) ; б) .

2. Построить графики функций:

а) (без нахождения точек перегиба, а также график производной по графику построенной функции);

б) .

3. Найти радиус основания и высоту прямого кругового цилиндра,

вписанного в сферу единичного радиуса и имеющего среди всех таких

цилиндров наибольшую полную поверхность.

4. Вычислить функции , используя формулу Лейбница.

5. Оценить с помощью формулы Тейлора абсолютную погрешность

приближенной формулы: , .

6. Составить уравнения касательной и нормали к графику функции ,

.

7. Составить уравнения касательной и нормали к графику функции

в точке .

8. Вычислить производную 2-го порядка от неявной функции: .

9. Вычислить производную 2-го порядка от функции, заданной параметрически:

10. Вычислить предел с помощью формулы Тейлора: .

11. Удовлетворяют ли функции и условиям теоремы

Коши на отрезке ?