Понятие функции - копия
.docПонятие функции.
Функция – понятие, отражающее связь между элементами множеств. Функция – это «закон», по которому каждому элементу одного множества (Область определения, аргумент) ставится в соответствие некоторый элемент другого множества (Область значение, значение).
Графики элементарных функций
-
Пропорциональные y = k*x. График – прямая линия, проходящая через начало координат
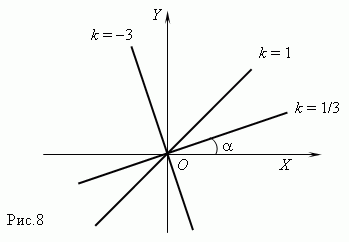
-
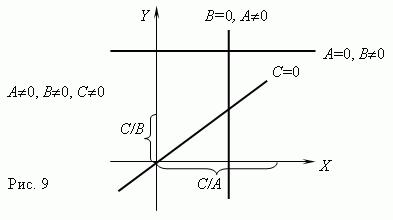
Линейные A x + B y = C. График – прямая линия.
-
Обратно пропорциональные
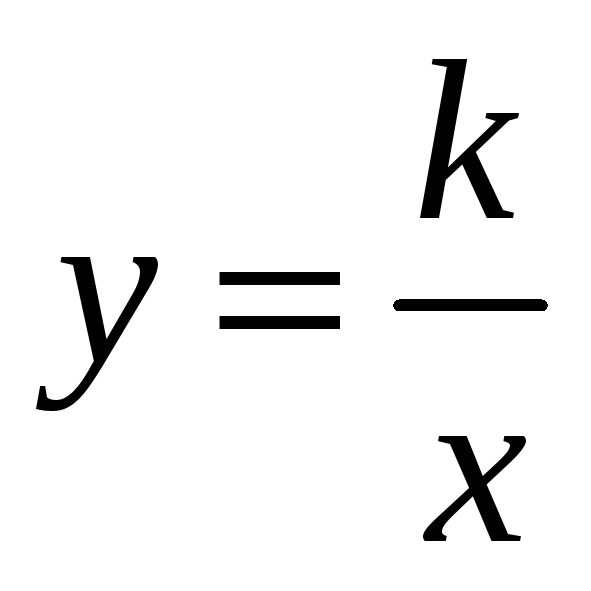 .
График – гипербола.
.
График – гипербола.
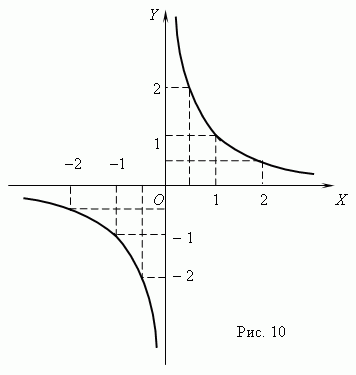
-
Квадратичные y = ax 2 + bx + c, где a, b, c - постоянные, a ≠ 0. График - квадратная парабола. Вершина –
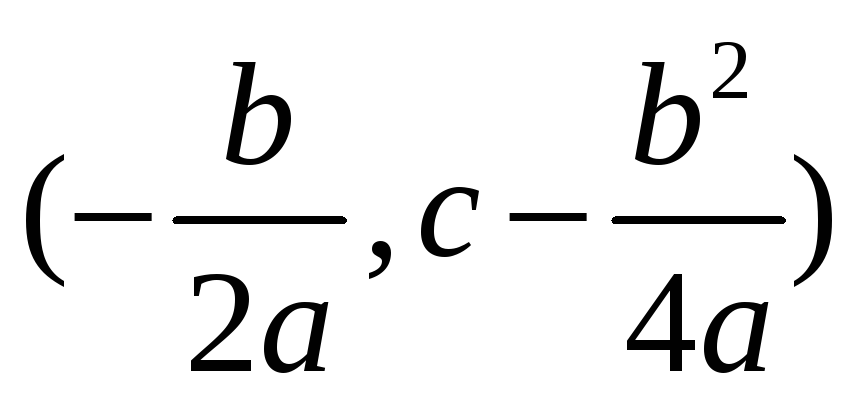

-
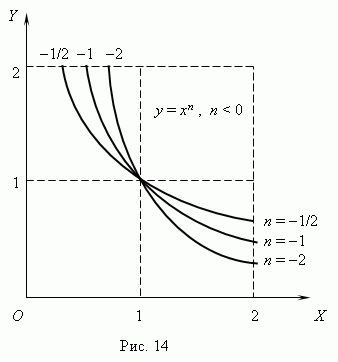
Степенные y = axn

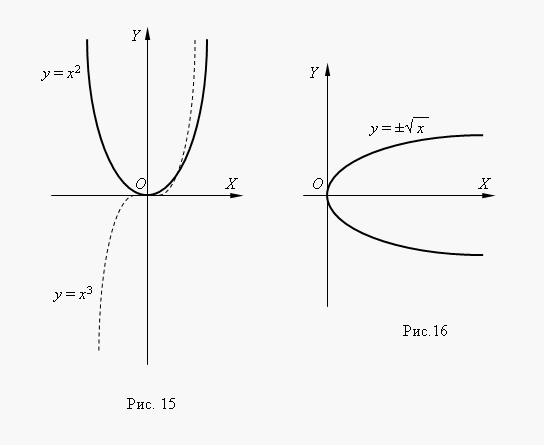
-
Показательные y = ax
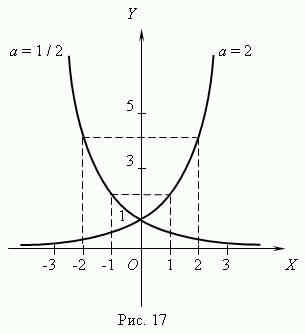
-
Логарифмические y = loga x
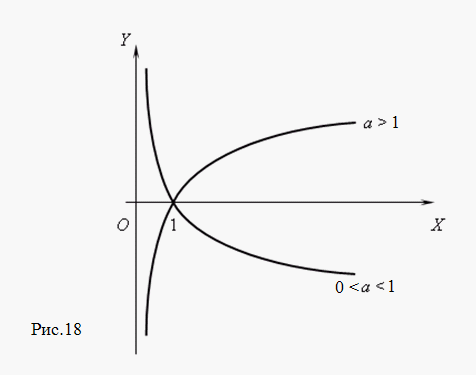
-
Тригонометрические
-
1. y = sin x. График – синусоида.
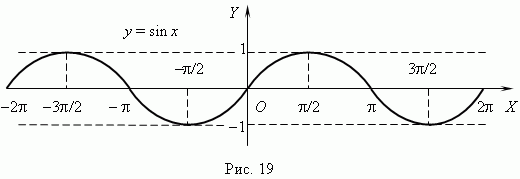
2. y = cos x. График – косинусоида.
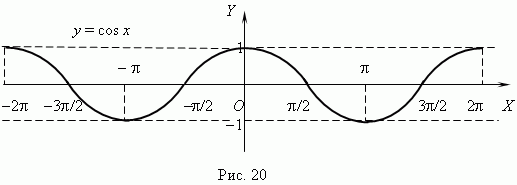
3. y = tg x; y = ctg x

-
Обратные тригонометрические (аркфункции)
y = Arcsin x, y = Arccos x
y = arcsin x, y = arccos x
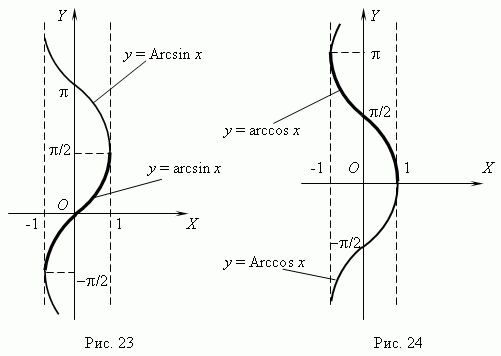
y = Arctan x, y = Arccot x
y = arctan x, y = arccot x
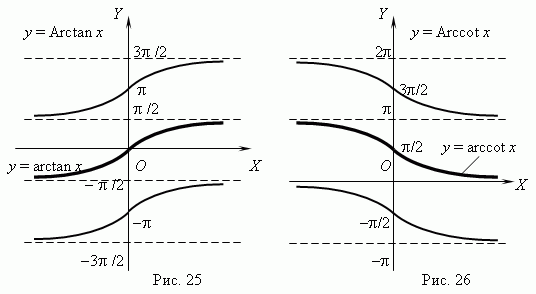
Монотонная функция - это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Пусть дана функция
![]() Тогда
Тогда
функция f называется возрастающей на M, если
![]() .
.
функция f называется строго возрастающей на M, если
![]() .
.
функция f называется убывающей на M, если
![]() .
.
функция f называется строго убывающей на M, если
![]() .
.
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат). Периодическая функция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).
Взаимно-однозначное отображение – отображение, при котором каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отношение, которое обладает тем же свойством.
Обратная функция – функция, обращающая зависимость, выражаемую данной функцией.
Функция
![]() является обратной к функции
является обратной к функции
![]() ,
если выполнены следующие тождества:
,
если выполнены следующие тождества:
f(g(y)) = y для всех
![]()
g(f(x)) = x для всех
![]()
Сложная функция – Функция, имеющая в качестве аргумента результат другой функции, «функция от функции».
Предел функции – величина, к которой стремится функция при стремлении её аргумента к заданной точке. Определение Коши:
Число А называется пределом функции
f(x) при х
стремящемся к х0 если для любого
положительного
найдется такое положительное ,
что для всех х принадлежащих интервалу
|х-х0|<, будет
выполнено условие |f(х)-А|
< :
![]()
Геометрический смысл предела функции:
![]() ,
если для любой ε-окрестности точки А
найдется такая δ-окрестность точки хо,
что для всех х¹х0 из этой
δ-окрестность соответствующие значения
функции ƒ(х) лежат в ε-окрестности точки
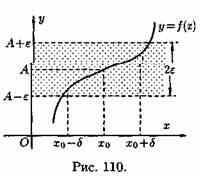
А. Иными словами, точки графика функции
у=ƒ(х) лежат внутри полосы шириной 2ε,
ограниченной прямыми у=А+ ε , у=А-ε (см.
рис. 110). Очевидно, что величина δ зависит
от выбора ε, поэтому пишут δ=δ(ε).
,
если для любой ε-окрестности точки А
найдется такая δ-окрестность точки хо,
что для всех х¹х0 из этой
δ-окрестность соответствующие значения
функции ƒ(х) лежат в ε-окрестности точки
А. Иными словами, точки графика функции
у=ƒ(х) лежат внутри полосы шириной 2ε,
ограниченной прямыми у=А+ ε , у=А-ε (см.
рис. 110). Очевидно, что величина δ зависит
от выбора ε, поэтому пишут δ=δ(ε).
Вычисление пределов. Раскрытие неопределенностей.
Методы вычисления пределов функций,
заданных формулами, которые в результате
формальной подстановки в них предельных
значений аргумента теряют смысл, то
есть переходят в выражения типа:
![]() по
которым невозможно судить о том,
существуют или нет искомые пределы, не
говоря уже о нахождении их значений,
если они существуют.
по
которым невозможно судить о том,
существуют или нет искомые пределы, не
говоря уже о нахождении их значений,
если они существуют.
Подобные неопределенности можно вычислить с помощью правила Лопиталя, либо с помощью разложение Тейлора.
Замечательные пределы.
Первый замечательный предел:![]()
Второй замечательный предел:
![]() или
или![]()
Односторонний предел
Предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Бывает левосторонним и правосторонним.
Число
![]() называется правосторонним пределом
[левосторонним пределом] функции
называется правосторонним пределом
[левосторонним пределом] функции
![]() в точке a, если для
всякого положительного числа
отыщется отвечающее ему положительное
число такое, что
для всех точек x из
интервала
в точке a, если для
всякого положительного числа
отыщется отвечающее ему положительное
число такое, что
для всех точек x из
интервала
![]() [
[![]() ]
справедливо неравенство
]
справедливо неравенство
![]() .
.
Непрерывность функции на отрезке и в точке.
Функция f(x)
непрерывна в точке
![]() если
предел в точке x0
равен значению функции в этой точке,
если
предел в точке x0
равен значению функции в этой точке,
![]() .
Функция
непрерывная в каждой точке промежутка
(a,b)
называется непрерывной на промежутке.
.
Функция
непрерывная в каждой точке промежутка
(a,b)
называется непрерывной на промежутке.
Функция непрерывна на отрезке [a,b], если она непрерывна в каждой точке интервала (a; b) и, кроме того, непрерывна справа в точке a и слева в точке b.
Функция непрерывная на отрезке [a,b] достигает на нем своих наибольшего и наименьшего значений.
Непрерывность сложной функции.
Если функция f непрерывна в точке a и функция g непрерывна в точке f(a), то сложная функция g(f(x)) непрерывна в точке a. Непрерывная функция от непрерывной функции
есть функция непрерывная.
Доказательство:
По условию теоремы, f
непрерывна в a, поэтому
![]() .
.
Далее, по условию, g
непрерывна в f(a),
поэтому
![]() .
Полученное равенство и означает, что
сложная функция g(f(x))
непрерывна в точке a.
■
.
Полученное равенство и означает, что
сложная функция g(f(x))
непрерывна в точке a.
■
Классификация точек разрыва функции.
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
1.Функция f(x) имеет точку разрыва первого рода при x = a, если в это точке
-
Существуют левосторонний предел
 и правосторонний предел
и правосторонний предел
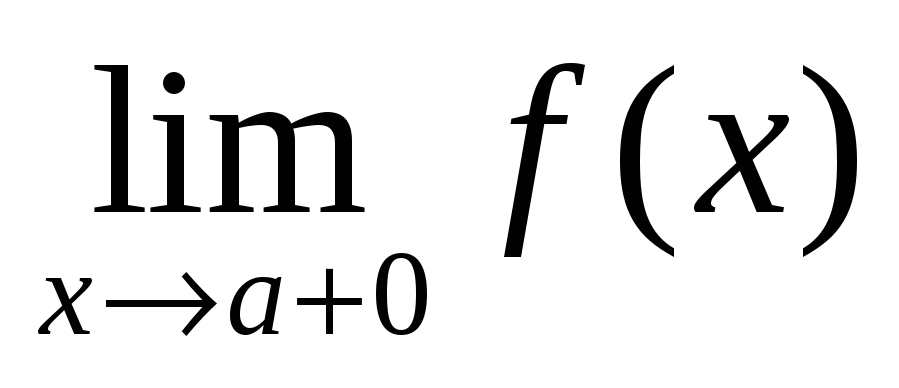 ;
; -
Эти односторонние пределы конечны.
При этом возможно следующие два случая:
-
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
-
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая точка называется точкой конечного
разрыва. Модуль разности значений
![]() односторонних
пределов называется скачком функции.
односторонних
пределов называется скачком функции.
2.Функция f(x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности
Бесконечно малые и бесконечно большие функции.
бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
бесконечно большая функция – это функция, предел которой в данной точке равен бесконечности определенного знака.
Теоремы о бесконечно малых.
-
Для того чтобы
 необходимо
и достаточно
необходимо
и достаточно
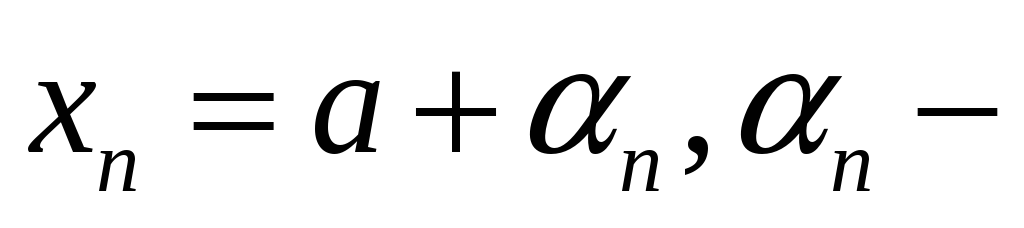 бесконечно
малая.
бесконечно
малая. -
Результат произведения бесконечно малой на бесконечно малую есть бесконечно малая.
-
Сумма конечного числа бесконечно малых — бесконечно малая.
Понятие эквивалентных бесконечно малых.
Если
![]() ,
то бесконечно малые величины α и β
называются эквивалентными (
,
то бесконечно малые величины α и β
называются эквивалентными (![]() ).
).
Использование бесконечно малых при нахождении пределов.
При замене бесконечно малой функции эквивалентной эй функцией предел отношения не изменится. Таблица эквивалентных бесконечно малых: