
7.4 Интегральное исчисление
7.4.1. Укажите условия, при выполнении которых функция F(x) является первообразной для функции f(x) на промежутке X:
Варианты ответа:
1) F(x) = f(x) для любого x X;
#2) F (x) = f(x) для любого x X;
3) F(x) = f (x) для любого x X;
4) F(x) – f(x) = С для любого x X, где С — некоторая константа;
5)
F (x) =![]() f(x)
для любого x X.
f(x)
для любого x X.
7.4.2. Совокупность всех первообразных для функции f(x) на промежутке X называется:
Варианты ответа:
#1) неопределенным интегралом от функции f(x);
2) определенным интегралом от функции f(x);
3) несобственным интегралом от функции f(x);
4) подынтегральной функцией;
5) подынтегральным выражением.
7.4.3. Если F1(x) и F2(x)- первообразные функции f(x) на промежутке X, то
Варианты ответа:
1) F1(x) = С F2(x), где С - некоторая константа;
2) F1(x) + F2(x) = С, где С - некоторая константа;
#3) F1(x) – F2(x) = С, где С - некоторая константа;
4)
F1(x) =  ,
где С
- некоторая константа;
,
где С
- некоторая константа;
5)
F1(x) =  ,
где С
- некоторая константа.
,
где С
- некоторая константа.
7.4.4.Пусть F(x) произвольная первообразная для функции f(x) на промежутке (–; +). Тогда:
Варианты ответа:
1) если f(x) - четная функция, то F(x) - нечетная функция;
2) если f(x) - нечетная функция, то F(x) - нечетная функция;
3) если f(x) - периодическая функция, то и F(x)- периодическая функция;
4) если f(x) - четная функция, то F(x) - четная функция;
#5) если f(x) - нечетная функция, то F(x) - четная функция.
7.4.5. Множество функций {arcsin x + C} задается неопределенным интегралом вида:
Варианты ответа:
1)
![]() ;
;
2)
![]() ;
;
#3)
 ;
;
4)
 ;
;
5)
![]() .
.
7.4.6. Из приведенных интегралов выберите ˝неберущиеся˝ интегралы:
Варианты ответа:
#1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
4)
![]() ;
;
5)
![]() .
.
7.4.7. Укажите верные равенства:
Варианты ответа:
1)
![]() ;
;
2)
![]() ;
;
#3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
7.4.8. Укажите верные равенства:
Варианты ответа:
1)
![]()
#2)
![]()
3)
![]()
4)
![]()
5)
![]()
7.4.9. Если функция f(x) имеет первообразную на промежутке X, то для произвольного k на этом промежутке верно:
Варианты ответа:
1)
![]()
2)
![]()
3)
![]() ;
;
#4)
![]()
5)
![]()
7.4.10. Укажите верные утверждения:
Варианты ответа:
1)
![]()
2)
![]()
#3) если F(x) является первообразной для функции v(x) u (x) на промежутке X, то v(x) u(x) – F(x) является первообразной для функции v (x) u(x) на промежутке X;
4) если функция v(x) u (x) является первообразной для функции F(x) на промежутке X, то v(x) u(x) – F(x) является первообразной для функции v (x) u(x) на промежутке X;
5)
![]()
7.4.11. Отметьте те интегралы, которые удобно вычислять методом интегрирования по частям:
Варианты ответа:
1)
![]()
2)
![]()
3)
![]()
#4)
![]()
5)
![]()
7.4.12. Отметьте те интегралы, которые удобно вычислять методом интегрирования по частям:
Варианты ответа:
1)
![]()
#2)
![]()
3)
![]()
4)
![]()
5)
![]()
7.4.13. Среди приведенных интегралов отметьте те, для которых при интегрировании по частям удобно выбрать u(x) = x:
Варианты ответа:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
#5)
![]()
7.4.14. Укажите верные равенства (f(x) — произвольная, интегрируемая на отрезке [a; b] функция):
Варианты ответа:
1)
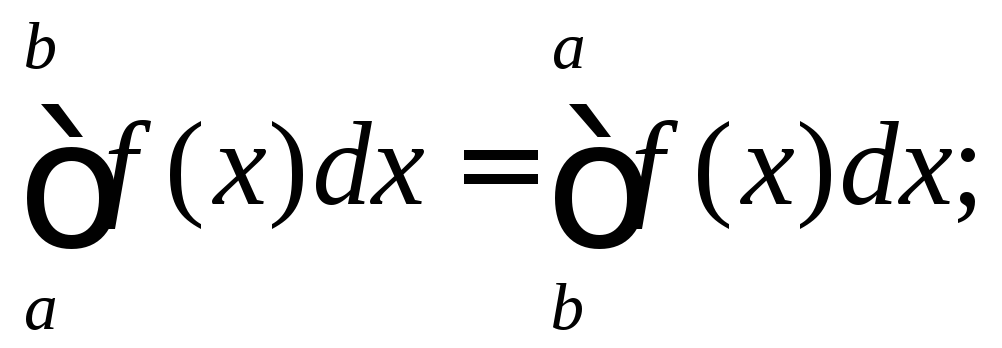
2)

#3)

4)

5)

7.4.15. Следующих условий достаточно, чтобы гарантировать интегрируемость функции f(x), определенной на отрезке [a; b]:
Варианты ответа:
1) монотонность f(x) на отрезке [a; b];
2) ограниченность f(x) на отрезке [a; b].
3) конечное число точек разрыва на отрезке [a; b];
#4) непрерывность f(x) на отрезке [a; b];
5) неограниченность f(x) на отрезке [a; b].
7.4.16. Пусть f(x) и g(x) — произвольные интегрируемые на отрезке [a; b] функции. Тогда:
Варианты ответа:
1)
если f(x) g(x)
для всех x [a; b],
то
 ;
;
#2)
 .
.
3) если функция f 2(x) интегрируема на отрезке [a; b], то и f(x) интегрируема на этом отрезке;
4)
если f(x) < g(x)
для всех x [a; b],
то
 ;
;
5) если функция f(x) интегрируема на отрезке [a; b], то и функция f(x) интегрируема на этом отрезке;
7.4.17. Пусть f(x) интегрируема на отрезке [0; 1] причем для всех x [0; 1] выполняются неравенства 1 f(x) 4. Тогда:
Варианты ответа:
1)

#2)

3)

4)

5)

7.4.18. Пусть f(x) — произвольная интегрируемая на отрезке [a; b] функция. Тогда:
Варианты ответа:
1)
если f(x) ≤ 0
на отрезке [a; b],
то
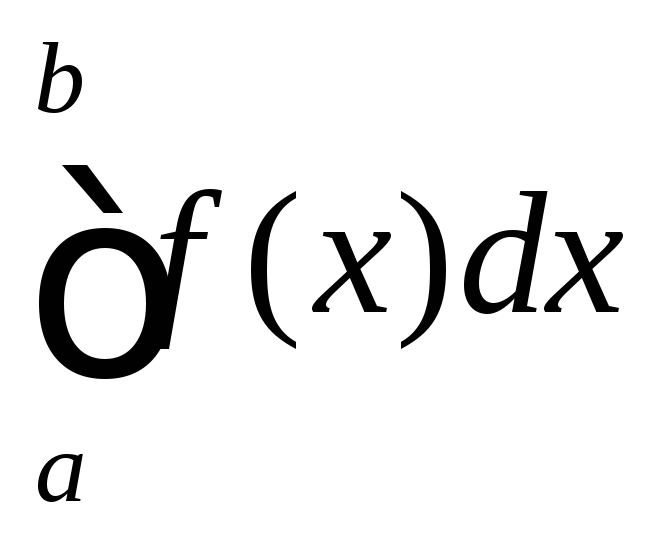 равен площади фигуры, ограниченной
прямыми
равен площади фигуры, ограниченной
прямыми![]() ,
,![]() ,
,![]() и графиком функцииy =f(x);
и графиком функцииy =f(x);
2)
если m
и М —
минимальное и максимальное значения
функции на отрезке [a; b],
то
 ;
;
3)
если m
- минимальное значение функции на отрезке
[a; b],
то
 ;
;
#4)
если f(x) 0
на отрезке [a; b],
то
 равен площади фигуры, ограниченной
прямыми
равен площади фигуры, ограниченной
прямыми![]() ,
,![]() ,
,![]() и графиком функцииy = f(x);
и графиком функцииy = f(x);
5)
если М —
максимальное значение функции на отрезке
[a; b],
то
 .
.
7.4.19. Пусть функция f(x) интегрируема на отрезке [a; b]. Интегралом с переменным верхним пределом называется:
Варианты ответа:
1)
совокупность всех первообразных функции
f(x)
на отрезке
![]() ;
;
#2)
функция
 ,
определенная для всех
,
определенная для всех![]() ;
;
3)
число, равное
 ;
;
4)
совокупность всех интегрируемых функции
f(x)
на отрезке
![]() ;
;
5)
![]() .
.
7.4.20. Если F(x) —первообразная для произвольной функции f(x), непрерывной на отрезке [a; b], то
Варианты ответа:
1)
 ;
;
#2)
 ;
;
3)
 ;
;
4)
 ;
;
5)
 .
.
7.4.21.
Пусть произвольная функция f(x)
непрерывна на отрезке [a; b],
а функция (t)
непрерывна на отрезке [; ]
и
![]() .
Тогда:
.
Тогда:
Варианты ответа:
#1)
 ;
;
2)
 ;
;
3)
 ;
;
4)
 ;
;
5)
 .
.
7.4.22. Какой интеграл равен площади области, изображенной на рисунке

Варианты ответа:
1)
 ;
;
2)
 ;
;
#3)
 ;
;
4)
![]() ;
;
5)
![]() .
.
7.4.23. Какой интеграл равен площади области, изображенной на рисунке

Варианты ответа:
1)
 ;
;
2)
 ;
;
3)
 ;
;
#4)
 ;
;
5)
 .
.
7.4.24. Какой интеграл равен площади области, изображенной на рисунке

Варианты ответа:
1)
 ;
;
2)
 ;
;
3)
 ;
;
4)

#5)
 .
.
7.4.25.
Если
![]()
![]() первообразная
для
первообразная
для![]() ,
то
,
то![]() равен
равен
Варианты ответа:
1)
![]() ;
;
2)
![]() ;
;
#3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
7.4.26.
Если
 ,
то
,
то![]() равен
равен
Варианты ответа:
1)
![]() ;
;
2)
![]() ;
;
#3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
7.4.27.
Если на
![]() верно
верно![]() ,
то выполняется неравенство
,
то выполняется неравенство
Варианты ответа:
#1)
 ;
;
2)
 ;
;
3)
 ;
;
4)
 ;
;
5)
 .
.
7.4.28.Если
на рисунке
 дуга АВ
дуга АВ![]() это
график функции
это
график функции![]() ,
то площадь заштрихованной фигуры
вычисляется по формуле
,
то площадь заштрихованной фигуры
вычисляется по формуле
Варианты ответа:
1)
 ;
;
2)
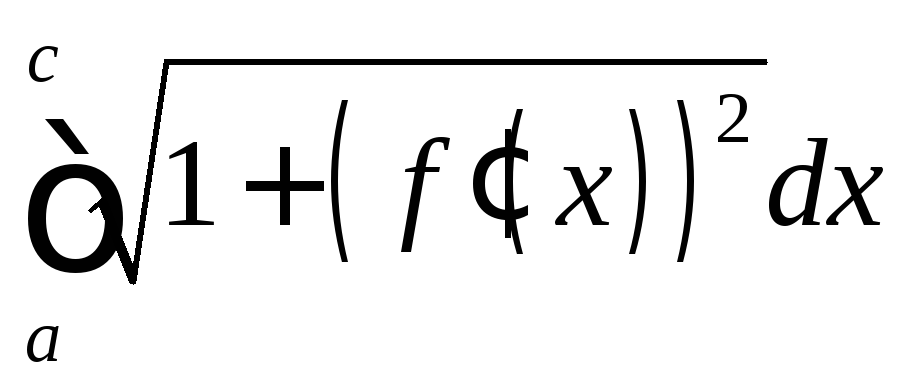 ;
;
3)
 ;
;
4)
 ;
;
#5)
 .
.
7.4.29.
Если на
рисунке
 дуга АВ
дуга АВ![]() это
график параметрически заданной функции
это
график параметрически заданной функции![]() ;
;![]() ,
,![]() ,
то длина этой дуги вычисляется по
формуле
,
то длина этой дуги вычисляется по
формуле
Варианты ответа:
#1)
 ;
;
2)
 ;
;
3)
 ;
;
4)
 ;
;
5)
 .
.
7.4.30.Интеграл
вида
![]() в случае
в случае![]() вычисляется путем подстановки:
вычисляется путем подстановки:
Варианты ответа:
1)
![]() ;
;
#2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
7.4.31.
Интеграл вида
![]() в случае
в случае![]() вычисляется путем подстановки:
вычисляется путем подстановки:
Варианты ответа:
#1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
7.4.32.
Интеграл вида
![]() в случае
в случае![]() вычисляется путем подстановки:
вычисляется путем подстановки:
Варианты ответа:
1)
![]() ;
;
2)
![]() ;
;
#3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
7.4.33.
Интеграл вида
![]() вычисляется с помощью универсальной
подстановки:
вычисляется с помощью универсальной
подстановки:
Варианты ответа:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
#4)
![]() ;
;
5)
![]() .
.
