
- •Тема 1 Предмет и метод статистики: определение, области применения, основные понятия
- •1.1 Статистика как форма практической деятельности. Статистика как наука: определение, области применения. Основные разделы статистической науки.
- •1.2. Объект, признаки совокупности, их виды. Методы статистики. Закон больших чисел и его роль в статистике. Генеральная и выборочная совокупности.
- •1.3 Методология и методы статистики.
- •1.4 Понятие официальной и неофициальной статистики. Ошибки при сборе и обработке статистического материала.
- •Тема 2. Статистические наблюдение, группировка, таблицы, графики
- •2.3. Статистическая сводка: определение, виды сводок (простая, сложная, централизованная и децентрализованная), программа проведения.
- •2.4. Статистическая группировка. Задачи группировок. Рекомендации по проведению группировок.
- •2.6. Табличный метод в статистике.
- •2.7. Графический метод в статистике
- •Тема 3. Абсолютные и относительные величины
- •3.1 Значение для управления и принципы формирования системы показателей статистики
- •Признаки классификации статистических показателей
- •3.2 Абсолютные величины: определение, виды: индивидуальные, сводные (объемные), расчетные. Единицы измерения абсолютных показателей.
- •Тема 4. Вариационные ряды, показатели вариации
- •4.2. Показатели вариации для характеристики вариационных рядов
- •4.3. Средние величины: определение; основное условие их применения; виды средних (простых и средневзвешенных). Правило мажорантности средних.
- •4.4. Дисперсия: способы ее расчета, виды дисперсии, правило сложения дисперсии.
- •4.5. Мода и медиана: определение, основное условие для применения, расчет показателей для дискретных и непрерывных вариационных рядов.
- •4.6. Симметричные и асимметричные распределения. Показатели асимметрии и эксцесса для характеристики асимметричных рядов распределения.
- •Тема 5. Выборочное наблюдение
- •5.2 Определение способом повторного и бесповторного отбора по генеральной совокупности средней, предельной и относительной ошибок средней с учетом заданного доверительного интервала.
- •5.4 Понятие малой выборки. Определение средней и предельной ошибок по малой выборке с учетом заданного доверительного интервала.
- •Тема 6. Индексный метод
- •6. 1 Индексный метод: определение, области применения, виды индексов
- •Признаки классификации экономических индексов
- •6.3 Индексный анализ динамики среднего уровня ряда (арифметического и гармонического индексов). Индексы качественных показателей (переменного, постоянного состава, структурных сдвигов).
- •Тема 7. Ряды динамики
- •7.1 Понятие и классификация рядов динамики: основные элементы и виды
- •7.3 Методы выявления тенденций (метод укрупнения интервалов, метод скользящей средней).
- •Тема 8. Статистические методы изучения взаимосвязи между явлениями. Корреляционно-регрессионный анализ.
- •8.2 Корреляционно-регрессионный анализ: области применения, основные этапы и требования проведения анализа.
- •8.3 Корреляционно-регрессионный анализ: аналитическое выражение уравнения (прямолинейной, криволинейной) регрессии для однофакторной корреляционно-регрессионной модели.
- •8.5 Показатели тесноты корреляционной связи для многофакторной корреляционно-регрессионной модели.
5.2 Определение способом повторного и бесповторного отбора по генеральной совокупности средней, предельной и относительной ошибок средней с учетом заданного доверительного интервала.
Чтобы получить суждение о точности результатов выборочного наблюдения, математическая статистика дает аппарат характеристики состава генеральной совокупности и формулу средней ошибки, т.е. средней величины из всех возможных ошибок при бесчисленном множестве случайных выборок.
Средняя ошибка выборки для средней величины признака определяется по формуле:
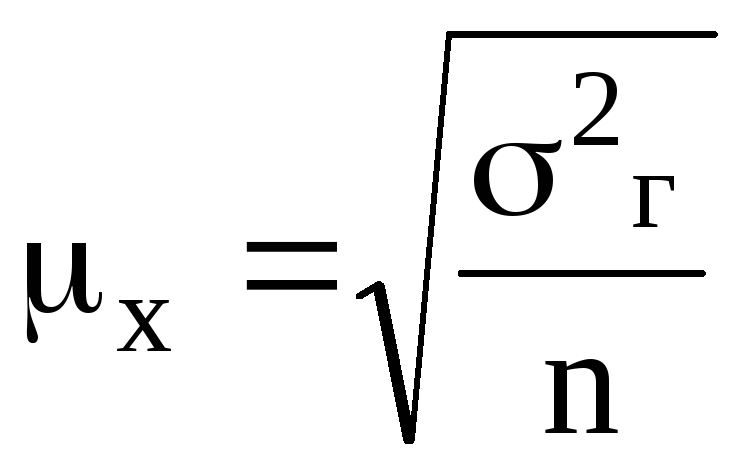 ,
,
где 2г – дисперсия количественного признака в генеральной совокупности.
Если при выборочном наблюдении изучению подлежит альтернативный признак (доля признака), то средняя ошибка выборки для доли единиц, обладающих данным признаком, определяется по теореме Я. Бернулли:
![]() ,
,
где p – доля единиц, обладающих данным качеством, в генеральной совокупности; p(1-p) – дисперсия альтернативного признака в генеральной совокупности.
Средняя ошибка выборки по значениям выборочной дисперсии 2 для средней и w(1–w) для доли признака при повторном способе выборки определяется по формуле:
![]() ,
,
![]() ,
где w – доля признака в выборочной
совокупности.
,
где w – доля признака в выборочной
совокупности.
На практике повторная выборка, при которой численность генеральной совокупности остается неизменной и для каждой единицы вероятность попасть в выборку одинакова, встречается редко (например, при изучении населения в качестве пользователей, пациентов, избирателей).
При бесповторной выборке численность генеральной совокупности в процессе отбора сокращается на 1–n/N, где n/N – доля отобранных единиц. В связи с этим формулы средней ошибки выборки приобретают следующий вид:
![]() ;
;
![]() .
.
Так как доля единиц генеральной совокупности, не попавших в выборку (1–n/N), всегда меньше единицы, то ошибка выборки при бесповторном отборе при прочих равных условиях меньше, чем при повторном отборе.
Как и сама выборочная характеристика, ошибка выборки является случайной величиной, она может быть в каждом конкретном случае меньше, равна или больше . Академик А.М. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения:
![]() ,
,
где ∆ - предельная ошибка выборки, t – коэффициент доверия, зависящий от вероятности (Р), с которой предельная ошибка определяется, - средняя ошибка выборки.
Значения функции Ф(t) табулированы при разных значениях, например:
при t=1 P() = Ф(1) = 0,683;
при t=2 P(2) = Ф(2) = 0,9545;
при t=3 P(3) = Ф(3) = 0,9973 и т.д.
В общем виде = t* характеризует предельную ошибку выборки, показывающую максимально возможное расхождение выборочной и генеральной характеристик при заданной вероятности этого утверждения. Так, при t=2 возможная ошибка не превысит 2, что гарантируется с вероятностью 0,9545. Это значит, что в 9545 выборках из 10000 подобных максимальная ошибка не выйдет за пределы 2.
При проведении выборочного учета массовых социально-экономических явлений считается достаточным максимальный размах 3.
Возможная ошибка выборки указывается с определенной вероятностью Р, с которой гарантируются границы рассчитанной случайной ошибки репрезентативности. На практике наиболее часто пользуются значениями вероятности Р=0,95 (t=1,96), Р=0,99 (t=2,58) и Р=0,999 (t=3,28), гарантирующими репрезентативность выборки соответственно с ошибкой 5; 1; 0,1%.
Возможная ошибка выборки позволяет определять предельные значения характеристик генеральной совокупности при заданной вероятности, т.е. их доверительные интервалы. Поэтому вероятность Р называется доверительной, она представляет собой вероятность того, что ошибка выборки не превысит некоторую заданную величину . Доверительные интервалы для:
генеральной
средней -
![]() (от
(от![]() до
до![]() ),
),
генеральной
доли –
![]() (от w–
до w+).
(от w–
до w+).
Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется отношением предельной ошибки средней или доли к соответствующей характеристике выборочной совокупности:
![]() %;
%;
![]() %.
%.
При проведении выборочного наблюдения в экономических исследованиях преимущественно стремятся к тому, чтобы относительная ошибка репрезентативности выборки не превышала 5 ... 10%.
5.3 Определение необходимого объёма выборки для обеспечения репрезентативности выборочных наблюдений при повторном и бесповторном способе отбора. Виды отбора (случайный, механический, типический, стратифицированный, комбинированный).
Необходимый
объем выборки (![]() )определяется
из формул предельных ошибок выборки ,
соответствующих различным способам
отбора.
)определяется
из формул предельных ошибок выборки ,
соответствующих различным способам
отбора.
Так, для случайного повторного отбора имеем:
x
=
![]() , откуда
, откуда![]() .
.
Уменьшение (увеличение) предельной ошибки в несколько раз ведет к увеличению (уменьшению) выборочной совокупности в квадрат раз. Для уменьшения предельной ошибки, например, в 2 раза численность выборки должна быть увеличена в 4 раза. Из трех параметров два (t и ) задаются исследователем.
При
бесповторном
отборе
необходимая численность выборки
рассчитывается по формуле:
![]() .
.
При прочих равных условиях при бесповторном отборе требуется меньший объем выборочной совокупности, чем при повторном.
При изучении альтернативного признака (доли р) необходимый объем выборки определяется по формулам при отборе:
повторном:
![]() ,
бесповторном:
,
бесповторном:![]() .
.
Репрезентативность выборки зависит не только от количества отобранных единиц совокупности и степени их колеблемости по изучаемым признакам, но и от способа отбора.
В зависимости от способа выборки единиц из генеральной совокупности различают следующие виды отбора (выборки):
собственно случайный; механический;
типический (районированный, стратифицированный);
серийный (гнездовой); комбинированный, многофазный и др.
При собственно случайном отборе единицы отбираются из генеральной совокупности в строгом соответствии с научными принципами и правилами случайного отбора.
Формировать выборку в строгом соответствии с правилами случайного отбора практически очень сложно. Используются таблицы случайных чисел, нумеруются все единицы генеральной совокупности, при жеребьевке на каждую единицу заготавливаются соответствующие карточки или фишки. При большой генеральной совокупности проводить такую предварительную работу практически невозможно и нецелесообразно.
Для удобства проведения выборочного наблюдения на практике применяют другие формы отбора, организуемые таким образом, чтобы была обеспечена случайность выборки.
При механическом отборе генеральная совокупность делится на n равных частей в соответствии с естественным расположением ее границ (географическим, пространственным, алфавитным и др.) и из каждой части обследуется одна единица. Например, если нужно отобрать 10% рабочих, то обследуют каждого десятого рабочего по списку, упорядоченного по алфавиту. Ошибки репрезентативности при механическом отборе возникают не в результате случайности отбора, а в результате случайности размещения единиц изучаемой совокупности.
Если единицы в генеральной совокупности размещены случайно в отношении изучаемого признака (в алфавитном порядке, в порядке времени поступления писем, телеграмм, телефонных соединений), то ошибка механической выборки становится случайной и ее можно определять по формуле ошибки случайной выборки. Механический отбор удобно проводить, когда уже имеются списки единиц совокупности и когда имеют дело с генеральной совокупностью, численность которой известна лишь приблизительно и единицы которой появляются постепенно, например, при контроле качества услуг и средств связи.
Типический (районированный, стратифицированный) отбор осуществляется на основе предварительного разделения единиц генеральной совокупности на типические группы (районы, страты) по изучаемым признакам. В качестве групп, страт в зависимости от характера изучаемого признака могут использоваться округа, регионы, отрасли, предприятия. Отбор из каждой группы может осуществляться в случайном (повторном или бесповторном) или механическом порядке.
Объем выборки в каждой типической группе обычно устанавливается пропорционально ее удельному весу в генеральной совокупности или дифференцированному признаку. Это повышает точность выборочного наблюдения, поскольку более точно, чем при собственно случайной выборке, отражается структура генеральной совокупности.
При
типической выборке устраняется влияние
межгрупповой вариации изучаемого
признака на точность ее результатов,
так как имеется представительство в
выборочной совокупности каждой из
типических групп. Средняя ошибка выборки
здесь зависит не от общей дисперсии 2,
а от средней из групповых дисперсий
![]() .
Так как средняя из групповых дисперсий
всегда меньше общей дисперсии, при
прочих равных условияхошибка
типической выборки меньше ошибки
собственно случайного отбора.
.
Так как средняя из групповых дисперсий
всегда меньше общей дисперсии, при
прочих равных условияхошибка
типической выборки меньше ошибки
собственно случайного отбора.
При
определении ошибки типической выборки
в случае пропорционального
отбора для
расчета предельной
ошибки
выборки применяется формула случайной
выборки, в которой применяется средняя
из групповых дисперсий
![]() .
.
∆ = t*µ или для выборки:
повторной
-
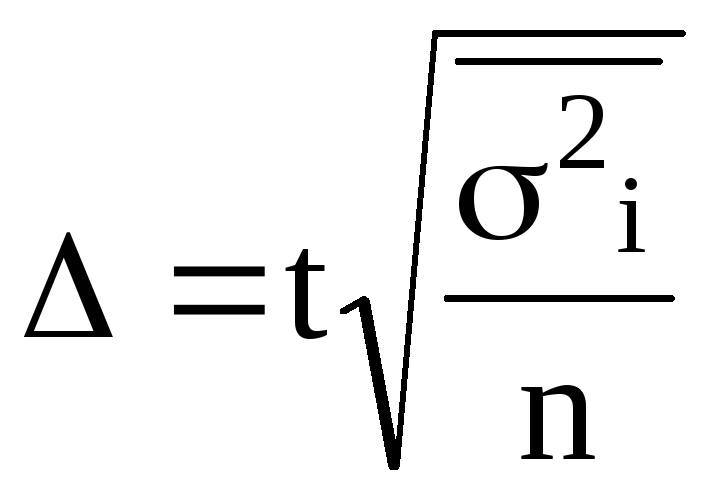 ; бесповторной -
; бесповторной -
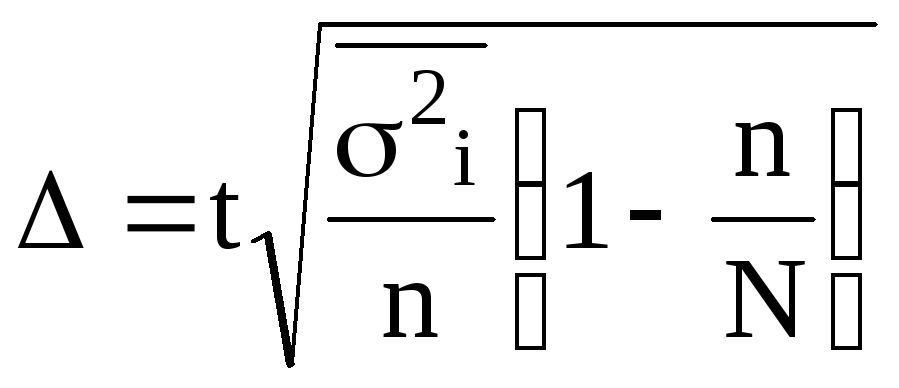 .
.
Отбор
единиц в типическую выборку производится
пропорционально объему типических
групп:
![]() ,
,
где
![]() =2ini/ni;
ni
– численность единиц выборочной
совокупности i-й группы; 2i
– выборочная дисперсия i-й группы; N
– объем всей совокупности;
=2ini/ni;
ni
– численность единиц выборочной
совокупности i-й группы; 2i
– выборочная дисперсия i-й группы; N
– объем всей совокупности;
![]() -
объем типических групп.
-
объем типических групп.
При определении ошибки типической выборки в случае отбора по дифференциальному признаку для расчета предельной ошибки выборки применяется формула случайной выборки, в которой применяется внутригрупповые дисперсии 2i.
∆ = t*µ или для выборки:
повторной
-
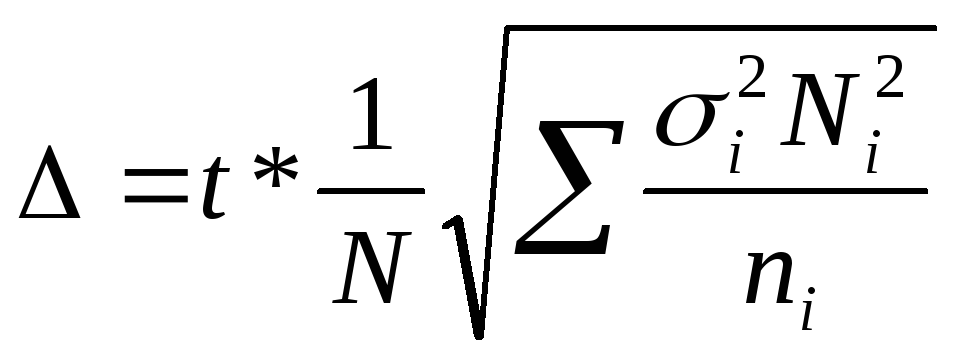 ; бесповторной -
; бесповторной -
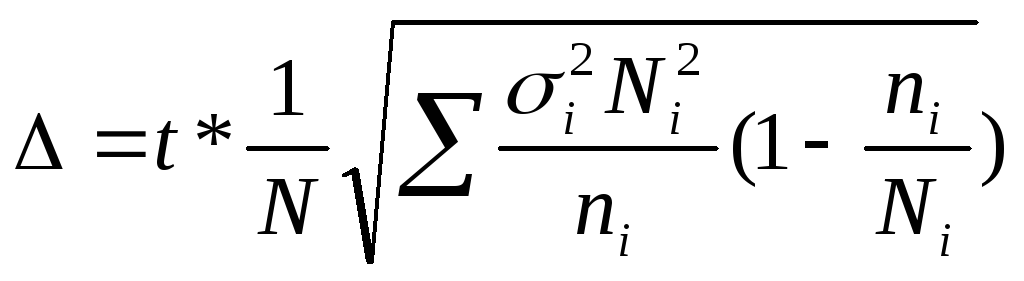 .
.
Отбор
единиц в типическую выборку производится
пропорционально дифференциальному
признаку - среднему квадратическому
отклонению
![]() :
:
![]() .
.
Выделение типических групп в генеральной совокупности значительно повышает репрезентативность выборки.
Примером типической выборки является уровень потребления услуг связи с разделением потребителей на население и организации с разбивкой последних на две группы – бюджетные и хозрасчетные.
При серийном (гнездовом) отборе в случайном порядке отбираются не единицы, а группы единиц (серии, гнезда). Серии, или группы, единиц отбираются по принципу случайного отбора или механическим способом, внутри отобранных серий (гнезд) обследованию подвергаются все единицы. Если общее число серий в генеральной совокупности обозначить через R, а число отобранных серий – r, то средняя ошибка выборки может быть определена по формулам:
x
=
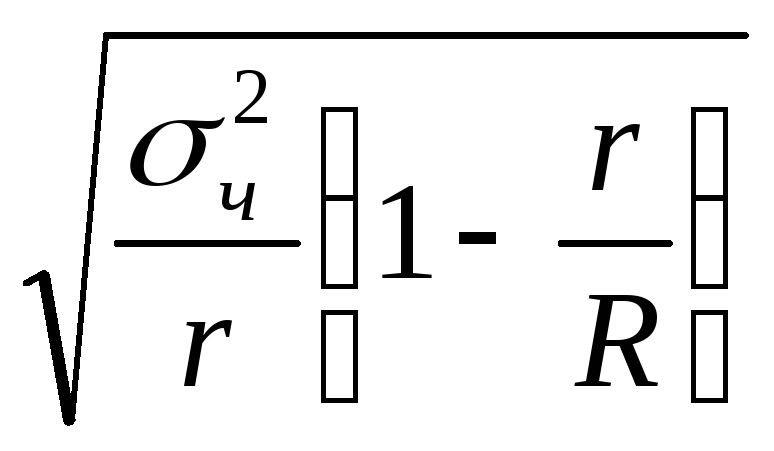 для бесповторной выборки, x
=
для бесповторной выборки, x
=
![]() ,
повторной выборки,
,
повторной выборки,
где
![]() –
межсерийная (межгрупповая) дисперсия.
–
межсерийная (межгрупповая) дисперсия.
Объём
серийной выборки определяется по
формуле:
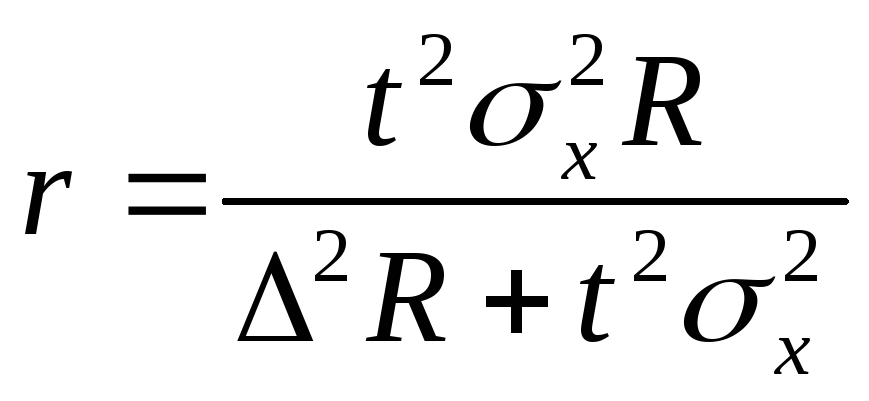
Чем меньше серийные средние отличаются одна от другой, т.е. чем ближе друг к другу серии по уровню изучаемого признака, тем точнее серийная выборка.
При значительной вариации серийных средних увеличивается ошибка репрезентативности выборки.
Серийная выборка применяется в организациях связи для определения скорости пересылки письменной корреспонденции и телеграмм, доли неисправных таксофонов, массы писем, объема передаваемой информации электронных сообщений и т.д. В качестве серии здесь выступает совокупность писем, телеграмм, разговоров за сутки, количество суток (дней) обследования равно количеству серий, попавших в выборочную совокупность.
На практике в зависимости от цели и задач выборочного обследования часто выборки производят на основе сочетания двух и более способов, образующих ступени отбора: механический и серийный, типический и механический, серийный и собственно случайный. Такие выборки получили название комбинированных (ступенчатых). При комбинированном отборе общая ошибка выборки состоит из ошибок на каждой ее ступени. Например, единовременно скорость прохождения письменной корреспонденции учитывается с помощью трех способов, образующих три ступени отбора: на основе случайного отбора определяются регионы страны, механического отбора – города и сельские населенные пункты регионов, серийного отбора – группы писем, представляющие определенные направления пересылки и подлежащие сплошному учету.
