Матрицы.

Впервые это понятие появилось в работах английских математиков Гамильтона

(1805 – 65) и Кэли (1821 – 95).

Матрицей называется прямоугольная таблица, составленная из чисел.

У матрицы, как и у определителя, различают строки, столбцы, элементы. Для краткости матрицы обозначаются буквамиА, В,С,…. В общем виде

Если число строк матрицы равно числу столбцов, то матрица называется квадратной.

Матрица, у которой все элементы равны нулю, называется нулевой.

Квадратная матрица вида называетсяединичной.

Определитель этой матрицы равен единице (det E = 1).Например,

Действия над матрицами.

1. Суммой матриц одинакового размера А +В =

называется матрица вида А+ В =

.

2. Произведением матрицы А на число α называется матрица вида

3. Умножение матриц осуществляются по правилу

=.

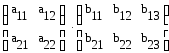Элемент с_ij, стоящий вi– той строке иj– том столбце, представляет собой сумму произведений элементовi– той строки первого множителя на элементыj– того столбца второго множителя

Число столбцов первого множителя равняется числу строк второго.

Если умножается матрица размером (m,n) на матрицу размером (n,p), то получается матрица размером (m,p).

П р и м е р.

Очевидно, АВ ≠ ВА. Можно доказать следующую теорему:

Если А и В квадратные матрицы, то det AB = det A ∙ det B.

Обратные матрицы.

Матрица А^-1называется обратной к А, еслиА^-1А = А∙А^-1 = Е.

Понятие обратной матрицы вводится только для квадратных матриц.

det A∙det A^-1 = det E = 1.

Теорема: Всякая невырожденная матрица имеет обратную.

Рассмотрим .Пусть ∆ =detA≠ 0 (матрица невырожденная).

Докажем, что , гдеA_{i j} - алгебраические дополнения элементовa_{i j}.A∙A^-1 =

Аналогично, А^-1∙А = Е. Следовательно А – обратная матрица.

П р и м е р .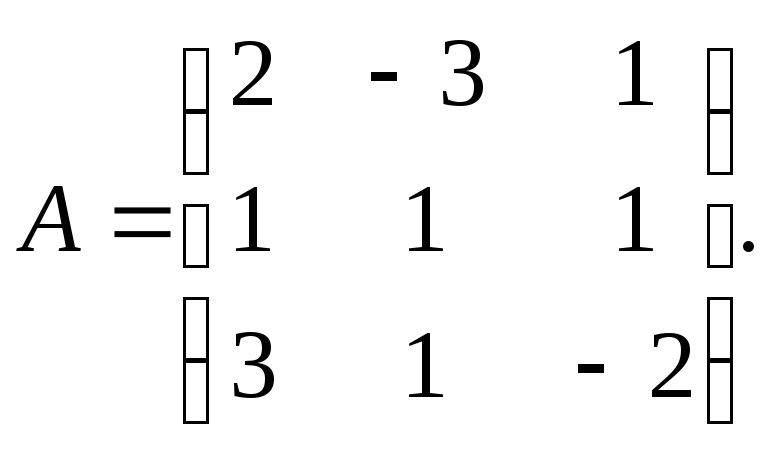Найти обратную матрицу А^-1.

Решение системы линейных уравнений матричным способом.

Рассмотрим систему mлинейных уравнений сmнеизвестными.

Тогда AX = B – матричная запись системы.

ПустьdetA≠ 0. Тогда существует обратная матрица А^-1.

Умножим систему слева на А^-1.

А^-1АХ = A^-1B, EX = A^-1B,

X = A-1B.

П р и м е р .

x + y - z = 0,

3x + 2y + z = 5,

4x – y + 5z = 3.

Правило Крамера.

Решая систему (1) матричным способом, получаем (m= 3)

Если ∆ ≠ 0, то система имеет единственное решение. Если ∆ =0, то система имеет либо бесконечное множество решений, либо не имеет решений вообще.

П р и м е р. Решить систему

3x + 2y + z = 5,

x + y - z = 0,

4x - y + 5z = 3.

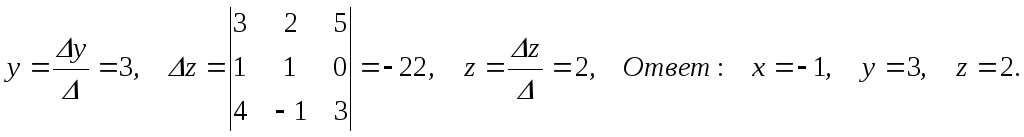
Метод Гаусса.

Правило Крамера используется только, если число уравнений не более трех. В противном случае оно приводит к громоздким вычислениям. В этом случае удобнее пользоватьсяметодом Гаусса,который заключается в последовательном исключении неизвестных. С помощью исключения неизвестных система (1) приводится к «треугольному виду»:

a₁′ x+b₁′y+c₁′z=d₁′,

b₂′y + c₂′z =d₂′,

c₃′z =d₃′ .

Затем, из третьего, второго и первого уравнений последовательно находятся значения x,yиz.

Рассмотрим предыдущую систему уравнений. Приведем ее к треугольному виду. Поменяем местами первое и второе уравнения.

x+y–z= 0x+y–z= 0,x+y–z= 0x+y–z= 0,

3x + 2y + z = 5, - y + 4z = 5, y – 4z = -5, y – 4z = -5,

4x - y + 5z = 3. – 5y + 9z = 3. -5y + 9z = 3. -11z =-22.

[2] –[1]∙3 , [3] – [1]∙4, [2]∙(-1), [3] + [2]∙5 [3]:11

x+y–z= 0 Обратный ходz= 2,y=-5 + 4z= 3,x=z–y= -1.

y – 4z=-5,

z = 2.

Практически удобнее приводить к треугольному виду не саму систему, а матрицу ее коэффициентов.

Ответ: z = 2,y= 3,x= -1.