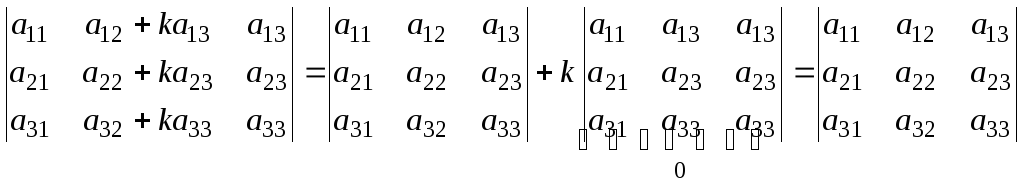12

Определители. Определители второго порядка.

Рассмотрим систему двух уравнений с двумя неизвестными.

a₁₁ x₁ + a₁₂ x₂ = b₁ , │∙ a₂₂

-

a₂₁ x₁ + a₂₂ x₂ = b₂. │∙ a₁₂

______________________

(a₁₁ a₂₂ – a₁₂ a₂₁) x = b₁ a₂₂ – a₁₂ b₂ , a₁₁ a₂₂ – a₁₂ a₂₁ ≠ 0.

Рассмотрим четыре числа, расположенных в виде квадратной таблицы.

а₁₁ а₁₂

а₂₁ а₂₂

Определителем второго порядка, соответствующим данной таблице, называется число, обозначаемое символом

и определяемое равенством

а_11, а₂₂- главная диагональ, а₁₂, а₂₁- побочная диагональ.

Решение системы имеет вид:

Определитель ∆ называется определителем системы.

Если ∆ ≠ 0, то система имеет единственное решение. Если ∆ = 0, то система либо не имеет решений вообще, либо имеет их бесконечное множество.

Определители третьего порядка.

Рассмотрим девять чисел, расположенных в виде квадратной таблицы. Определителем третьего порядка называется число, обозначаемое символом

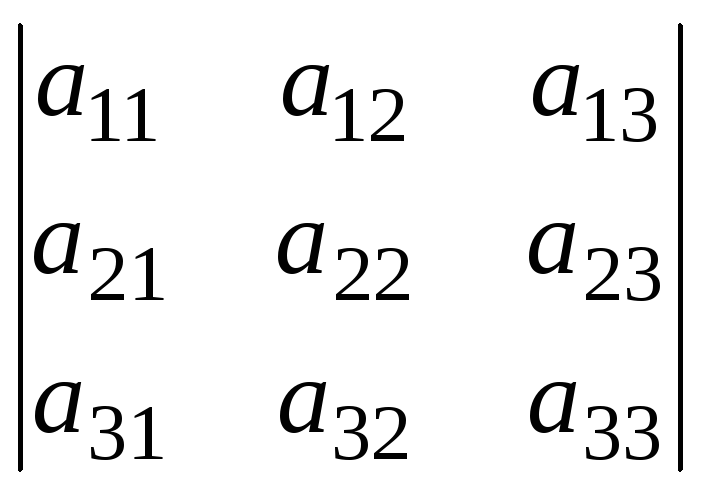и определяемое равенством

=

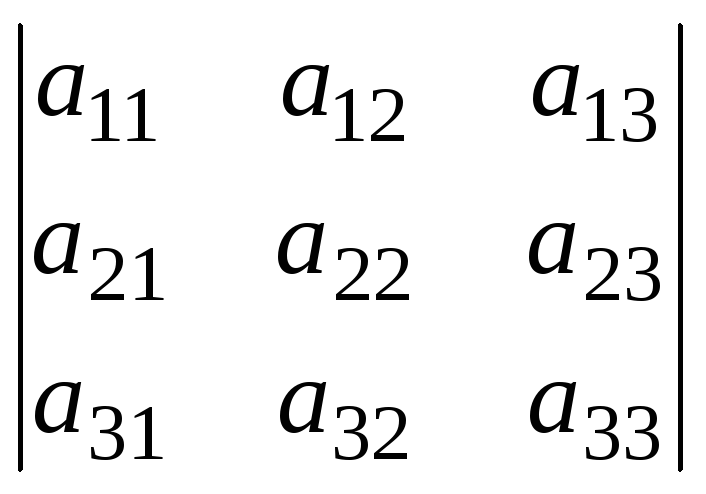a₁₁,a₂₂,a₃₃- главная диагональ,a₁₃,a₂₂,a₃₁– побочная диагональ.

Свойства определителей.

1. При замене строк столбцами величина определителя не изменится.

2. При перестановке двух строк (столбцов) определитель лишь меняет знак.

= -.

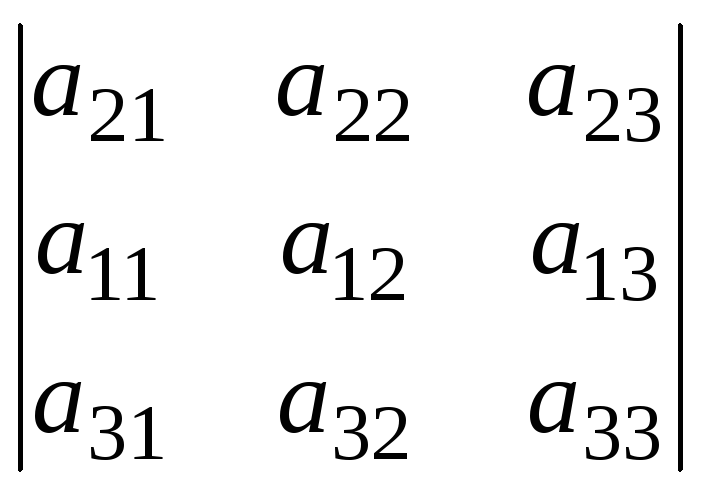3. Определитель с двумя одинаковыми строками (столбцами) равен нулю.

.

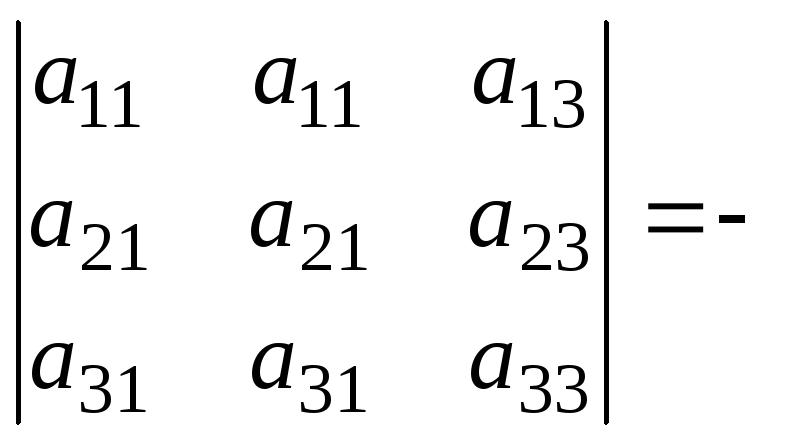
4. Рассмотрим некоторый элемент определителя. Вычеркнем строку и столбец, на которых стоит данный элемент. Оставшийся определитель второго порядка называется минором,соответствующим данному элементу.

Алгебраическим дополнениемэлемента определителя называется соответствующий ему минор, взятый со знаком(+), если сумма номеров строки и столбца четная, и со знаком(-), если эта сумма нечетная.

А_ij = (-1)^{i + j} M_ij

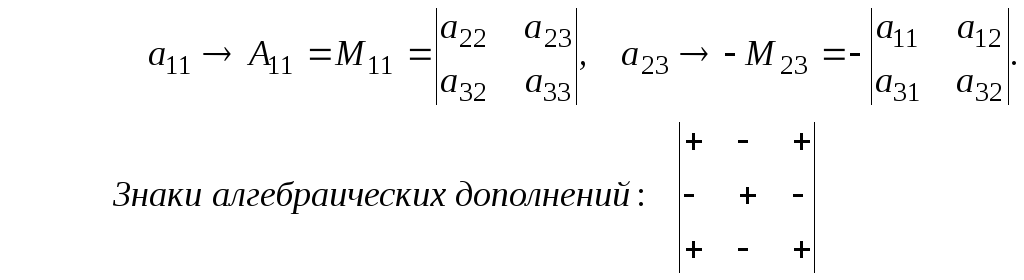
Сумма произведений элементов некоторой строки (столбца) определителя на алгебраические дополнения этих элементов равна определителю.

a₁₁ A₁₁ + a₁₂ A₁₂ + a₁₃ A₁₃ = ∆,

a₁₂ A₁₂ + a₂₂ A₂₂ + a₃₂ A₃₂ = ∆.

.

5. Сумма произведений элементов некоторого ряда (строки или столбца) определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

a₁₁A₁₂ + a₂₁ A₂₂ + a₃₁A₃₂ =.

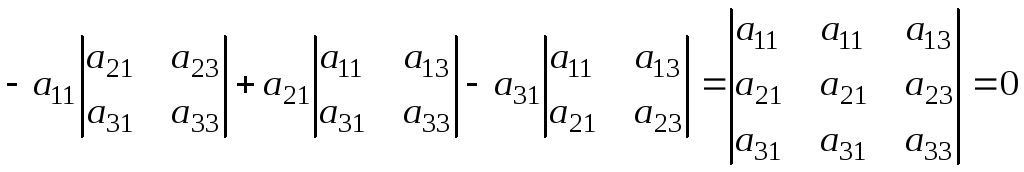(разложение определителя с двумя одинаковыми столбцами по элементам второго столбца).

5. Если все элементы некоторой строки или столбца определителя умножить на одно и то же число, то величина определителя умножится на это число.

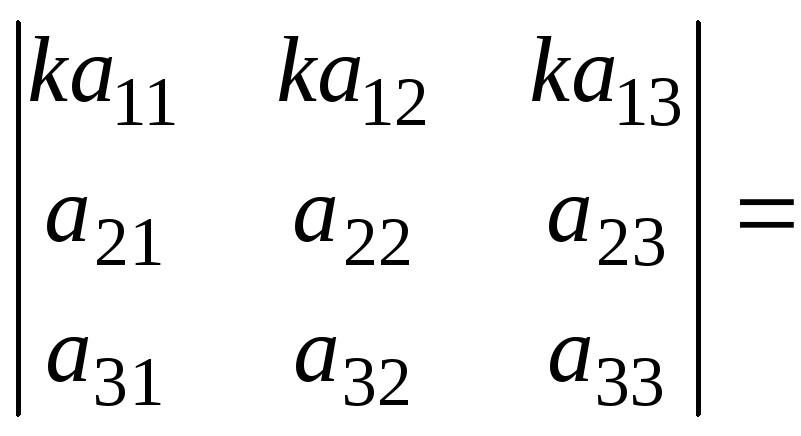k

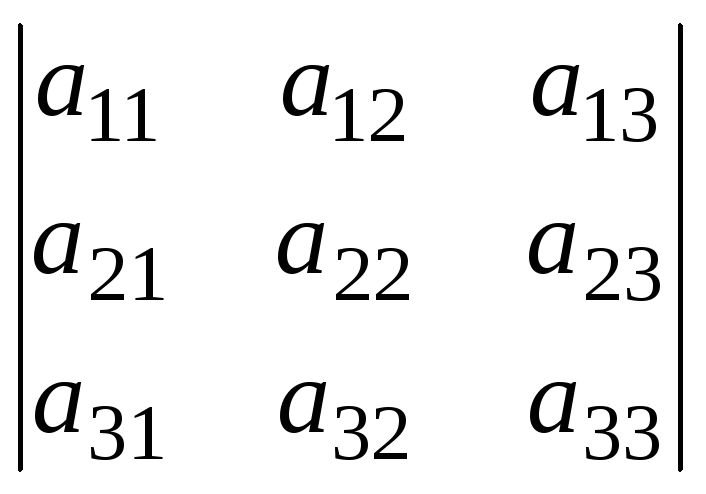
(справедливо для любой строки или столбца определителя).

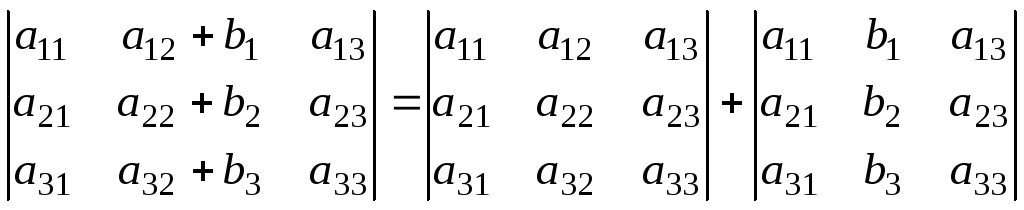7. (справедливо для любого ряда).

Следствие.Определитель не меняет своего значения, если ко всем элементам какого-нибудь ряда прибавить соответствующие элементы параллельного ряда, умноженные на любой общий множитель.