2.11. Потери предварительного напряжения арматуры

Первые потери:

• потери от релаксации напряжений арматуры

σ₁ = 0.03 · σ_sр = 0.03 · 500 = 15 MПа (1,5 кН/см²);

- потери предварительного напряжения вследствие температурного перепада принимаются равными нулю, т.к. прогрев бетона осущест­вляется в пропарочных камерах вместе с формами;

- потери предварительного напряжения от обжатия анкеров при электротермическом способе натяжения не учитываются; то же относится к потерям от деформации стальных форм;

- потери σ₆ предварительного напряжения из-за быстронатекающих деформаций ползучести бетона. Предварительно вычисляем усилие обжатия с учетом потерь:

P₁ = (σ_sр- σ₁) · A_sp = (50 – 1,5) · 5,09 = 304,6 кН.

Сжимающее напряжение в бетоне на уровне центра тяжести напря­гаемой арматуры в стадии предварительного обжатия вычисляется по формуле внецентренного сжатия:

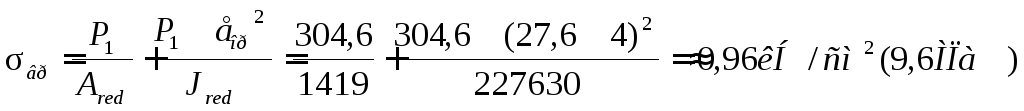
Так как σ _вр /R_вр = 9,6 / 18 = 0,53 < α , где α = 0,65 для бетона B30, то

σ ₆ = 0,85 · 40 · σ_вр /R_вр = 0,85 · 40 · 0,53 = 18,12 MПа = 1,8кН/см².

Первые потери: σ _los1 = σ₁ + σ _в =15 + 18,12 = 33,12 МПа.

Вторые потери:

-потери от усадки для бетона класса В30 σ₈ = 35 МПа;

-потери от ползучести бетона при σ_вр / R_вр < 0,75

σ₉ = 150 · 0,85 · σ_вр /R_вр =150 ·0,85 · 9,6 / 18 = 68 МПа.

Вторые потери составляют: σ _los2 = σ ₈ + σ ₉ = 35 + 68 = 103 МПа.

Все потери: σ _los = σ _los1 + σ _los2 = 33,12 + 103 = 136,12 МПа.

2.12. Вычисление изгибающего момента образования трещин

Момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин вычисляется по формуле:

M_crc= R_bt,ser · W_pl + M_rp ,

где M_rp - момент усилия Р относительно оси, нормальной к плос­кости изгиба и проходящей через ядровую точку, наиболее удален­ную от зоны, трещиностойкость которой проверяется.

Усилие обжатия вычисляется при коэффициенте точности натяже­ния A_sp < 1 с учетом всех потерь по формуле:

A_sp = 1- Δy_sp; ;

где n_р - число напрягаемых стержней, равное 2;

Р - предельно до­пустимое отклонение величины предварительного напряжения;

P = 30 + 360/l = 30 + 360/5,7 = 93 мПа;

l - длина натягива­емого стержня, равная 5,7м (расстояние между наружными гранями упоров);

Δy_sp = (0,5 · 93/500) (1 + 1/√2) = 0,17;

P₂ = (1 - Δy_sp )·( σ _sp - σ _los) · A_sp = (1-0,17)(50-13,6) · 5,09 = 189,7 кН.

Для нижней грани:

M_crc = R_bt,ser · W_pl + P₂(y₀ + r ) = 0,18·14430+(27,6 - 4 + 4,65 )·189,7 = 7960 кН·см = 79,56 кН·м.

2.13. Расчет на образование трещин

Трещины на нижней грани в стадии эксплуатации образуются, ес­ли не выполняется условие M_rM_crc.

Момент от внешних нагрузок относительно нижней ядровой точки M_r=97,97кH·м; М_r>М_crc = 79,56кHм и, следовательно, на нижней грани при эксплуатации будут образовываться трещины. Необходим расчет ширины раскрытия трещин.

Трещины на верхней грани при отпуске арматуры A_sp образуются, если

M_g + R_bt,scr · γ_bs · W_pl’ - γ_sp · (σ_sp - σ₁ - σ_b ) · A_sp (y₀ - a - r_inf) < 0,

М_g - момент от собственного веса панели, лежащей (условно) в момент отпуска натяжения на двух опорах, равный 11,42 кН·м. При проверке трещиностойкости верхней грани от действия усилия обжатия при изготовлении учитываются только первые потери, и усилие обжатия принимается с коэффициентом γ_b3.

γ_b2 = 1,2; γ_sp = 1 + Δγ_sp = 1 + 0,17 = 1,17.

11,42 + 1,2 · 0,18 · 27540 - 1,17 · (50 - 1,5 - 1,812) · 5,09 · (27,6 -4 -11) = 1630 кН·см > 0.

Трещины в верхней зоне не образуются. В данном случае из-за отсут­ствия указаний об условиях опирания панели при отпуске предварительного напряжения не учтено влияние собственной массы панели на трещиностойкость верхней грани сечения.