2.4. Определение усилий в элементах панели

В продольном направлении панель работает как балка на двух шарнирных опорах с расчетным пролетом =5450 мм и приведенным к тавровой форме поперечным сечением.

В середине пролёта действует максимальный момент от нагрузки:

M=(q’*l^2)/8=(38162,5*5,45^2)/8=141690 H*м=141,7кH*м

то же от нагрузки M=(50000*5,45^2)/8=185640H*м=185,64кH*м

то же от длительно действующей нагрузки

M=(25000*5,45^2)/8=9282H*м=92,82кH*м

то же от кратковременной нагрузки: 50000 - 25000=25000 Н/м:

M=(2,500*5,45^2)/8=92,82кH*м

Максимальное значение поперечной силы на опорах от нагрузки :

Q=q’*l/2=(38162,5*5,45)/2=104000H=104кH*м

В средних поперечных ребрах с расчетным пролетом l₀ = 1,27 м:

M=(q_o*l_o^2)/12 +(q^n * l_o^2)/8=(30000*1,27^2)/12 +(2370*1,27^2)/8=45100H*м

Q=(q_o*l_o)/4 +(q^n * l_o)/2=(30000*1,27)/4 +(2370*1,27)/2=11030H*м

При расчете плиты целесообразно задаться одинаковой несущей способностью всех сечений в пролетах и на опорах. Тогда моменты в этих сечениях квадратного отсека плиты в стадии образования пластических шарниров будут одинаковыми и в расчете на полосу шириной один метр определяются по формуле:

M=(q*l_o^2)/48=(2100+21600)*1,27^2 /48=796,34(H*м)/м

2.5. Расчет прочности панели в продольном направлении

по нормальным сечениям

Определяем предельно допустимую ширину сжатой полки b^'_f при­веденного сечения, используемую в расчете:

b_f = 2 · l₀/6 +b = 545/3 + 18 = 199см;

h₀ = 0,9 · h = 0,9·40 = 36см.

Так как фактическая ширина панели b_n = 149см меньше получен­ного значения, то принимаем b^'_f = 149см.

Предполагая, что нейтральная ось проходит в полке, вычисляем:

a_m=M/(y_b,1*R_b*b^'_f*h²_o)=141,7*100/(0,9*1,7*149*36^2)=0,0480.

По таблице "МУ" находим: ξ = 0,04 и ζ = 0,98.

Высота сжатой зоны:X= ξ·h₀=0,04·36 = 1,44см < h_f = 5 cм, следовательно, нейтральная ось действительно проходит в пределах сжатой полки.

Вычисляем граничное значение высоты сжатой зоны:

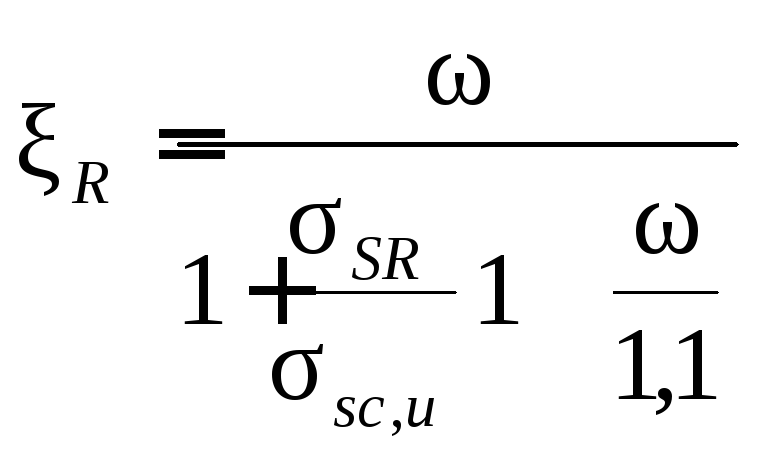
∆σ_sp = 1500 · σ_sp / R_s - 1200 = 1500 · 500/510 - 1200 = 270 МПа;

при γ_b2 = 0,9 σ_sc,u = 500 МПа.

Предварительное напряжение принимается с коэффициентом точно­сти натяжения:

γ_sp = 1- ∆ γ_sp = 1 - 0,1 = 0,9;

σ_sp = R_s,ser - P = 590 - (30 + 360/6) = 500 МПа;

σ_sp = R_s + 400 - σ_sp - ∆ σ_sp = 510 + 400 - 500 - 270 = 140 МПа.

Характеристика деформативных свойств бетона сжатой зоны для тяжелого бетона:

ω = 0,85 - 0,008 · R_b = 0,714.

Подставляя значения σ_SR, σ_sc,u и ω, получим:

.

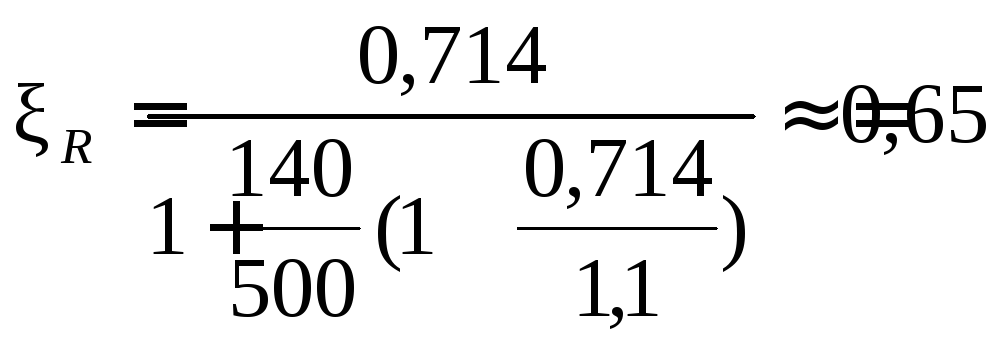При расчете прочности железобетонных элементов с высокопроч­ной арматурой и наличии неравенства ξ = 0,040 < ξ_R =0.65 расчетное сопротивление арматуры R_S должно быть умножено на ко­эффициент условия работы:

где - максимальное значение коэффициента, равное для стержневой арматуры 1,2.

При подстановке найденных значений ξ и ξ_R, получаем:

= 1,2 - (1,2 - 1)(2-0,04/0,65 - 1)=1,375 > .

Принято =I,2.

Площадь сечения растянутой арматуры:

Принимается арматура: 2 Ø18 А-IV с площадью 5,09 см².

В верхней зоне ребра конструктивно принимаем 2Ø12 A-I с площадью 2,26 см². Толщина защитного слоя бетона a_b составляет 20мм,

a = a_b+d/2 = 20 + 20/2 = 30мм, что примерно равно принятому значению a= 36мм.