ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ_учит

На общерекурсивные и рекурсивно перечислимые множества можно посмотреть следующим образом:

Множество А – общерекурсивно, если мы умеем «эффективно» решать проблему его разрешения, т.е. для любого натурального числа n мы может «эффективно» узнавать принадлежит ли n множеству А или нет. По этой причине общерекурсивные множества иногда называют разрешимыми множествами.

Проблемы нумерации

Ранее нам приходилось объектам некоторого фиксированного множества ставить в соответствие некоторое натуральное число, которое мы называли номером этого объекта. Так, например, мы нумеровали все машины Тьюринга. Рассмотрим множество целых неотрицательных чисел N = {0, 1, 2, ….}.

Естественно номером натурального числа n считать само это число.

Рассмотрим теперь N 2:

N 2 = {(a, b) / a N, b N} – множество всевозможных пар натуральных чисел.

Нумерация пар

Из теории множеств известно, что N 2 – счётно, т.е. все элементы из N 2 можно занумеровать натуральными числами так, что

1)каждой паре (a, b) из N 2 будет поставлено в соответствие одно и только одно натуральное число; оно и будет номером этой пары;

2)каждое натуральное число будет номером некоторой единственной пары.

Нам требуется указать какую-нибудь конкретную вычислимую нумерацию. Один из возможных способов (способ Кан-

тора) состоит в следующем.

Расположим все пары из N 2 в виде треугольной таблицы следующим образом:

119

……………………………………………..

(0; x+y) … (x; y) … (x+y; 0)

Теперь будем считать по порядку одну за другой строчки этой таблицы и присваивать парам соответствующие номера. Номер пары (a, b) будем обозначать через С(a, b). Т.о., полу-

чится: С(0; 0) = 0; С(0; 1) = 1; С(1; 0) = 2; … , С(7; 3) = 62, …

Этим способом можно решить поставленную задачу, но он является очень неэкономным, например, чтобы узнать С(100; 50) требуется выполнить довольно большую работу. Попытаемся вывести формулу для вычисления номера произвольной пары: С(x; y).

Способ построения таблицы с очевидностью подсказыва-

Вычислим номер пары (0; x+y). До неё в таблице расположены полностью заполненные строчки, в которых соответст-

венно: 1, 2,…, (x+y) штук пар. Тогда С(0; x+y) = 1+2+…+=

Двигаясь теперь по строке (*), через х шагов дойдем до

пары (x; y).

Получаем формулу: C x, y x y x y 1 x.

2

Тогда C 100,50 150 151 100 75 151 100 11425; 2

C 7,3 10 11 7 55 7 62 и т.д. 2

Решим обратную задачу: зная номер пары m, найти саму пару. Например, какая пара имеет номер 14?

Можно предложить следующую последовательность ша-

гов:

1) Вычитаем из m, m-1, m-2, … последовательно 1, 2, 3,… до тех пор , пока не получим число меньше, чем очередной член данной прогрессии: если m = 14, то получаем последовательность:

120

но 4<5, следовательно искомая пара находится в пятой строке.

а) Если окажется, что последнее число, например k, в последовательности равно числу, которое требуется вычесть, то искомая пара последняя в строке с данным номером: (k-1, 0).

б) Если число меньше, то искомая пара находится в k-той строчке. В этой строке k пар, значит мы знаем номер пары в строке. Из номера строки вычитаем номер пары в строке, получаем второе число пары. После этого из числа k-1 вычитаем y, получаем х. Пара найдена.

Рассмотрим первое слагаемое в формуле для С(x; y):

x y x y 1

2

Числа вида n n 1 получили название треугольных чисел. 2

Т.о., номер пары (x; y) - С(x; y), есть сумма некоторого треугольного числа t и х. Очевидно, что t С(x; y). Каким образом можно найти t?

Выпишем все треугольные числа меньшие 100:

0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91 (след. – 105)

+1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 +12 +13 +14

Какое из них будет искомым t x y x y 1 ? 2

Следующее за t треугольное число имеет вид:

x y 1 x y 2 x y x y 1 x.

2

Тогда, t С(x; y) < t1.

Значит, искомое треугольное число t таково, что следующее за ним треугольное число строго больше, чем С(x; y).

121

Обозначим ч/з n = x+ y;

n (n + 1)=20; n2+ n -20 = 0; n = 4 или n = - 5. n = 4. Составим систему условий:

x + y = 4,

x= С(x; y) - t,

y= n – x.

Например, если z = 100, то n(100) = 13; l(100) = 100-(13 14)/2 = 100-91 =9; r(100) = 4.

Действительно, С(9, 4) = 100. ((13 14)/2+9=100).

По определению функций С, l, r имеем: C(l(x), r(x)) = x.

Следует заметить, что функции C(x, y), l(x), r(x) – общерекурсивные.

122

Нумерация кортежей

Кортежем длины n называется упорядоченный набор чисел, а применительно к нашей теории – целых неотрицательных чисел (х1, х2, …, хn), xi N.

Обозначим номер такого кортежа Сn(х1, х2, …, хn). Номер пары С2(х1, х2), номер тройки С3(х1, х2, х3), … Сведем нумерацию троек к нумерации пар:

С3(х1, х2, х3) = С2(С2(х1, х2), х3):

вначале нумеруем пару первых двух чисел, а затем пару из полученного числа и третьего числа тройки.

Например, С3(2, 0, 5) = С2(5, 5) = 60.

Решим обратную задачу: по номеру тройки найти сам на-

бор.

Пусть n = 100: Обозначим: ll(n) – первое число, lr(n) – второе число,

rr(n) – третье число тройки,

имеющей номер n.

100 = С3(ll(100), lr(100), rr(100)) = С3(х1, х2, х3) = = С2(С2(х1, х2), х3).

Из предыдущего примера имеем, что С2(х1, х2) = 9, х3 = 4,

т.е. r(100) = 4; l(100) = 9.

100 = tn + С2(х1, х2), 100 = 91 + С2(х1, х2) С2(х1, х2) = 9.

х3 = 13 – 9 = 4.

9 = tn + х1; tn = 6. х1 = 9 – 6 = 3, х2 = 3 – 3 = 0.

Следовательно, номер 100 имеет тройка (3, 0, 4).

С3(3, 0, 4) = С2(С2(3, 0), 4) = С2(9, 4) = 13 14/2 + 9 = 100. С2(3, 0) = 3 4/2 +3 = 9.

Аналогично можно поступать для нумераций четвёрок, пятерок и т.д. n – ок натуральных чисел.

Пусть Сn(х1, х2, …, хn) – номер n – ки (х1, х2, …, хn), а lni y - i – тое число n – ки, имеющей номер y.

Тогда для n > 2 имеем:

123

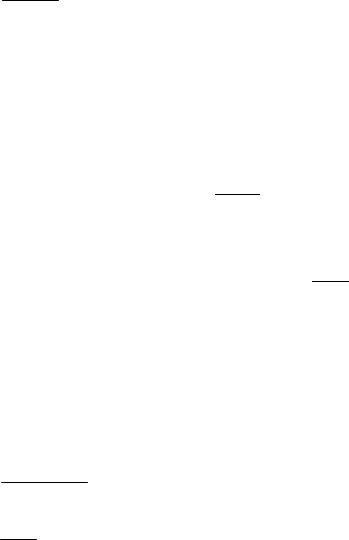
Сn(х1, х2, …, хn) = Сn-1(С2(х1, х2), х3…, хn),

ln1 y l21ln1 1 y , ln2 y l22ln1 1 y и lni y lni 11 y .

Пусть дано некоторое натуральное число. Например, N = 100. Номером какого кортежа оно является? Числа 100? или пары (9, 4)? или тройки (3, 0, 4)? и т.д.

Т.е. данное число должно нести в себе информацию о том, какова длина кортежа, номером которого оно является.

Сделаем это следующим образом: назовем число

А(х1, х2, …, хn+1) = С2(Сn+1(х1, х2,…, хn+1), n) номером кортежа (х1, х2,…, хn+1).

Например, вычислить А(1, 1, 0) = С2(С3(1, 1, 0), 2) =

= С2(14, 2) = 16 17 14 8 17 14 150. 2

Решим обратную задачу:

Дано: 100 = С2(y, 4). 100 – обобщенный номер набора длины 5 – С5(х1, х2, х3, х4, х5) = 9.

С5(х1, х2, х3, х4, х5) = С2(С4(х1, х2, х3, х4), х5) = 9. 9 = tn + С4 tn = 6 С4 = 3, n = 3.

С4 + х5 = n; 3 + х5 = 3 х5 = 0.

С4 = 3; по определению С2(С3(х1, х2, х3), х4) = 3

3 = tn + С3 tn = 3 3 = 3 + С3 С3 = 0, n = 2. С3 + х4 = 2 х4 = n – 0 = 2 – 0 = 2 х4 = 0.

С3(х1, х2, х3) = 0 (х1, х2, х3) = (0, 0, 0).

Искомая пятерка имеет вид:

(0, 0, 0, 2, 0) 100 = А(0, 0, 0, 2, 0). С5(0, 0, 0, 2, 0) = С2(С4(0, 0, 0, 2), 0) С4(0, 0, 0, 2) = С2(С3(0, 0, 0), 2)

С3(0, 0, 0) = 0

C 0,2 0 2 3 0 3 2

C 3,0 3 4 3 9 2

124

С5(0, 0, 0, 2, 0) = 9.

А(0, 0, 0, 2, 0) = С2(С5(0, 0, 0, 2, 0), 4) = С2(9, 4) =

13 14 9 13 7 9 100. 2

125