ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ_учит

Рекурсивные предикаты

Давая определение предиката, мы отмечали присущее этому понятию свойство функциональности. Предикат Р(х1, х2,…, хn) заданный на множестве Мn есть функция с областью определения Мn, принимающая значения в двухэлементном множестве {0, 1}.

В теории алгоритмов принято различать предикат Р и функцию, связанную с ним. Саму функцию называют характеристической (или представляющей) функцией предиката Р и обозначают Р.

0, если высказывание Р x1, x2 ,...xn ложно,

Т.о., P x1, x2 ,...xn

1, если высказывание Р x1, x2 ,...xn истинно.

Если M=N, то имеет смысл поставить вопрос о примитивной рекурсивности функции Р.

Опр. Предикат Р называется примитивно рекурсивным, если его характеристическая функция Р примитивно рекурсивна. Р называется рекурсивным, если Р – общерекурсивная.

Например, предикаты Р1(x,y) = (x=y); Р2(x,y) = (x<y) являются примитивно рекурсивными, так как их представляющие функции являются ПРФ.

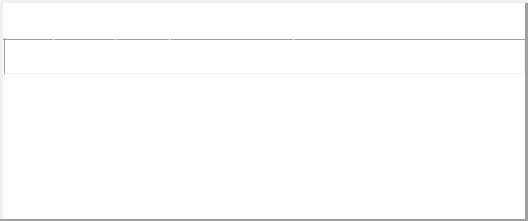
Действительно, в качестве представляющей функции первого предиката можно взять функцию вида Р1 (x) = sg|x-y|, где

является ПРФ.

Для предиката Р2(x,y) = (x<y) в качестве представляющей функции можно брать

2 x, y sg x y – она является ПРФ.

Теорема

Логические операции над предикатами сохраняют свойства примитивной рекурсивности предикатов.

Доказательство.

89

Приведем в виде таблицы истинностные значения логических операций: конъюнкции, дизъюнкции, импликации и отрицания.

Таблица 1. Результаты логических операций

P(x) P(x)Q(x)P (x)&Q(x)P(x) Q(x)P(x) Q(x)

Пусть Р(x) - представляющая функция предиката P(х);Q(x) - представляющая функция предиката Q(x), где в общем случае x = (x1, ..., xn).

Тогда нетрудно проверить, что следующие функции являются представляющими функциями для соответствующих логических операций относительно предикатов, представленных в таблице 1:

Р&Q = sg( Р(x) + Q(x));

Р Q = Р(x) Q(x);

Р Q = sg( Р(x)+ sg( Q(x)));

Р = sg( Р(x))

В качестве упражнения, проверьте самостоятельно, что представленные функции действительно удовлетворяют требуемому условию как представляющие функции предиката.

Ограниченные кванторы

Пусть задан двуместный предикат P(x,y), где в общем случае x = (x1, ..., xn).

90

Определение. Говорят, что предикат R(x,z) получен из предиката P(x,y) с применением операции навешивания ограниченного квантора существования, т.е. R(x,z) = ( y)y zP(x,y), если

R(x,z) = P(x,0) P(x,1) ... P(x,z)

Определение. Говорят, что предикат Q(x,z) получен из предиката P(x,y) с применением операции навешивания ограниченного квантора всеобщности, т.е. Q(x,z) = ( y)y zP(x,y), если

Q(x,z) = P(x,0) & P(x,1) & ... & P(x,z)

Пример. Пусть P(x,y) = (x+y=5). Рассмотрим

R(x,z) = ( y)y zP(x,y) и Q(x,z) = ( y) y zP(x,y). Очевидно:

Справедлива теорема

Теорема

Операция навешивания ограниченных кванторов существования и всеобщности сохраняет свойство примитивной рекурсивности функций относительно совокупности предикатов

{Р}.

Доказательство.

Пусть задан предикат Р(x,y) и Р(x,y) - представляющая его функция и пусть R(x,z) = ( y)y zР(x,y).

Представляющую функцию предиката R(x, z) обозначим через R(x,z) и покажем, что ее можно представить следующим образом:

z

R x, z P x, y

y 0

91

Действительно:

1. Пусть предикат R(x,z0) = и. Тогда по определению операции навешивания ограниченного квантора существования, найдется y0 такое, что 0 y0 z0 и Р(x,y0) = и, следовательно(x,y0) = 0. Отсюда следует, что:

z

R x, z P x, y 0.

y 0

2. Предположим, что предикат R(x,z0) = л. Тогда по определению операции навешивания ограниченного квантора существования, для любого набора (x,y) Р(x,y) = л, следовательно (x,y0) = 1 и

z

R x, z P x, y 1

y 0

Пусть Q(x,z) = ( y)y zР(x,y). Аналогично доказывается случай, когда задана операция навешивания ограниченного квантора всеобщности. Можно доказать, что в качестве представляющей функции предиката можно брать

и R(x,z) является ПРФ относительно совокупности { Р(x,y)} (докажите самостоятельно).

Пусть задана совокупность функций { 1, ..., k} и совокупность предикатов {Р1, ..., Рm}.

Определение. Функция f(x1, ..., xn) называется ПРФ относительно заданной совокупности функций и предикатов, если она ПРФ относительно совокупности = { 1, ..., m, Р1, ...,Рm}, где Рi - представляющая функция предиката Рi, 1 i m.

92

Кусочное задание функции

Одним из часто встречающихся, особенно в теории алгоритмов, способов задания функций является их задание с помощью так называемого оператора условного перехода. Этот оператор по функциям f1(х1, х2,…, хn) и f2(х1, х2,…, хn) и предикату Р(х1, х2,…, хn) строит функцию (х1, х2,…, хn):

f1 x1, x2 ,...xn , если высказывание Р x1, x2 ,...xn истинно,

x1, x2 ,...xn

f2 x1, x2 ,...xn , если высказывание Р x1, x2,...xn ложно.

Говорят ещё что функция (х1, х2,…, хn) – кусочнозаданная. С помощью характеристических функций предиката Р и его отрицания Р функцию (х1, х2,…, хn) можно представить следующим образом:

(х1, х2,…, хn) = f1(х1, х2,…, хn)· Р(х1, х2,…, хn) + + f2(х1, х2,…, хn)· Р(х1, х2,…, хn).

Справедлива теорема:

Т. Если функции f1, f2 и предикат Р примитивно рекурсивны, то и кусочно-заданная функция , построенная из f1, f2 и Р, примитивно рекурсивна.

Отсюда следует, что оператор условного перехода примитивно рекурсивен.

Оператор условного перехода может иметь и более общую форму, когда переход носит не двузначный, а многозначный характер и определяется конечным числом предикатов Р1, Р2,…, Рk, из которых истинен всегда один и только один предикат. И в такой форме оператор условного перехода примитивно рекурсивен, так как и в этом случае производимую им функцию можно представить в аналогичном виде:

(х1, х2,…, хn) = f1· Р1 + … + f1· Рk.

Это соотношение определяет функцию и в том случае, когда ни один из операторов Р1, Р2,…, Рk не является истинным: в этом случае значение рано нулю.

Этот факт позволяет доказать примитивную рекурсивность функций, заданных на конечных множествах, так как все их можно задать с помощью оператора условного перехода. При этом их приходится доопределять с помощью какой-либо

93

константы на всех остальных натуральных числах, на которых она не определена.

Например, функцию , определенную на множестве {1, 3, 9, 17} равенствами (1) = 8; (3) = 0; (9) = 4; (17) = 6 с по-

мощью оператора условного перехода можно описать следующим образом:

8, если х 1,

0, если х 3,

x

4, если х 9,

6, во всех остальных случаях.

Как уже было отмечено ранее, все примитивно рекурсивные функции всюду определены. Это следует из того, что всюду определены простейшие функции, а операторы суперпозиции и примитивной рекурсии это свойство сохраняют.

Следует отметить также, что мы имеем дело не с функциями, а с их примитивно рекурсивными описаниями. Различие здесь такое же, как и различие между булевыми функциями и их представлениями в виде формул. Примитивно рекурсивные описания разбиваются на классы эквивалентности: в один класс входят все описания, задающие одну и туже функцию. Задача распознавания эквивалентности примитивно рекурсивных описаний является алгоритмически неразрешимой.

Понятие машины Тьюринга.

Введение понятия машины Тьюринга явилось одной из первых и весьма удачных попыток дать точный математический эквивалент для общего интуитивного представления об алгоритме. Это понятие названо по имени английского математика, сформулировавшего его в 1937 г., за 9 лет до появления первой ЭВМ.

М.Т. есть математическая (воображаемая), а не физическая машина. Она моделирует некие реальные процессы. Тьюринг предпринял попытку смоделировать действия математика, осуществляющего некую умственную созидательную деятельность. Такой человек, находясь в определенном «умонастроении» просматривает некоторый текст. Затем вносит в

94

этот текст какие-то изменения, проникается новым «умонастроением» и переходит к просмотру последующих записей.

М.Т. действует примерно также. Ее удобно представлять в виде автоматически работающего устройства. В каждый дискретный момент времени устройство, находясь в некотором состоянии, обозревает содержимое одной ячейки, протянутой через устройство ленты, и делает шаг, заключающийся в том, что устройство переходит в новое состояние, изменяет содержимое обозреваемой ячейки и переходит к обозрению следующей ячейки: справа или слева. Причем шаг осуществляется на основании предписанной команды. Совокупность всех команд представляет собой программу машины Тьюринга.

Итак, машина Тьюринга состоит из:

1)ленты, разбитой на клетки (ячейки), ограниченной слева и потенциально неограниченной справа:

2)читающей и пишущей головки (каретки);

3)внешнего алфавита – конечного набора символов

S={s0, s1, …sn}. Среди них выделяют s0 – символ пустой ячейки;

Замечание: можно обойтись алфавитом, состоящм из 2-х символов S={0, 1}, где 0= s0 – символ пустой клетки.

4)Множества внутренних состояний или внутреннего алфавита Q={q0, q1, …, qm}. Среди этих состоя-

ний выделяют два: q1 – начальное состояние;

q0 – заключительное состояние;

5)Множества символов сдвига {л; н; п}: л – влево; н

– неподвижно; п – вправо.

Машина Тьюринга работает тактами (шагами). Эта работа описывается командами. Каждая команда имеет вид: saqb sczqd, z {л; н; п};

s S; q Q.

95

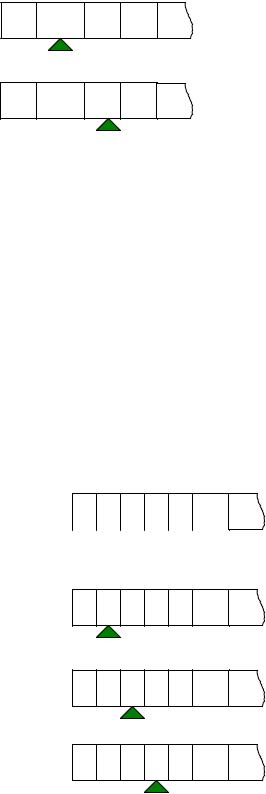
По этой команде читающая головка, находясь в состоянии qb и обозревая символ sa заменяет этот символ на sc, затем делает движение z на одну клетку и переходит в новое состояние

qd:

sa

qb

sс

qd z = п

Список всех команд МТ называется программой этой машины. Программу удобно записывать в виде таблицы, назы-

ваемой машинной таблицей:

Пример: Пусть работа машины описывается командами:

0q1 0пq2;

0q2 1пq2; начало;

1q2 1пq2.

1ый шаг;

2ой шаг;

3ий шаг.

96

На этой простой машине можно реализовать любой алгоритм.

Определение машинно-вычислимой функции. Примеры.

Будем рассматривать теоретико-числовые функции – это функции всюду определенные на N со множеством значений из N.

Примеры:

1)f1(x, y)=x+y – теоретико-числовая функция;

2)f2(x, y)=x y;

3)f3(x, y)=z z = НОД(x, y);

4)f4(x, y)=z z = НОК[x, y];

5)f5(x, y)=x-y – не является теоретико-числовой функци-

ей.

Замечание. Числа на ленте будут записываться в u–нарной системе счисления; u–нарная – значит при записи используется 1 символ, т.е. число изображается единичками или палочками.

Опр. Теоретико-числовая функция называется вычислимой на МТ, если существует машина Тьюринга со следующими свойствами:

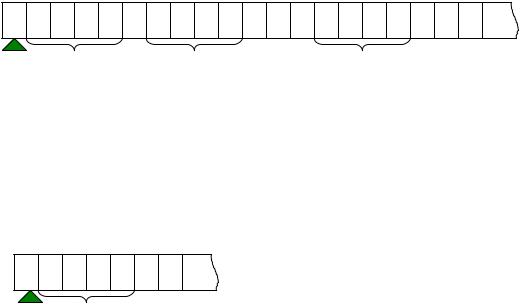
1)машина начинает работать со следующей ситуации (см. рис.) на ленте:

0 1 1 … 1 0 1 1 … 1 0 … 0 1 1 … 1

q1 x1 x2 xn

(на ленте имеется запись n аргументов функции). Читающая головка – под первой клеткой в состоянии q1. Такая ситуация называется стандартным восприятием n-ки чисел.

2)После конечного числа шагов машина останавливается, переходя в состояние q0, на ленте появляется запись:

0 1 1 … 1 0

q0 f(x1, x2, …, xn) – значение функции.

97

Читающая головка устанавливается под крайней левой клеткой в состоянии q0.

Примеры:

1). Построить машину Тьюринга, вычисляющую функ-

цию: (х) 0.

0 1 1 1 0

План:

1)читающая головка двигается вправо до ближайшей пустой клетки;

2)двигается влево, стирая единицы, на некотором шаге обозревает 0 и останавливается.

Начало

0q1

0пq2

-

Конец

98