
2.Дифференциальные уравнения
Задача №1. Найти общий интеграл дифференциального уравнения
![]()
Решение:Данное уравнение перепишем в виде:
![]() ,
далее
,
далее
![]() это дифференциальное уравнение ( в
дальнейшем ДУ) первого порядка с
разделяющимися переменными, т.е.
это дифференциальное уравнение ( в
дальнейшем ДУ) первого порядка с
разделяющимися переменными, т.е.

![]() или
или
![]() .
.
Ответ:
![]() - общий интеграл данного
ДУ.
- общий интеграл данного
ДУ.
Задача №2.Найти общий интеграл
дифференциального уравнения
![]()
Решение:
Данное уравнение является ДУ первого
порядка, однородным, т.к. его можно
привести к виду и
![]() однородная функция нулевого измерения
однородная функция нулевого измерения![]() и, сделав замену переменных
и, сделав замену переменных![]() ,
привести к виду
,
привести к виду![]() ,
далее вычисляя интеграл в левой части,
найти ответ. У нас
,
далее вычисляя интеграл в левой части,
найти ответ. У нас
![]() ;
;
![]() ;
;

![]() .Окончательно:
.Окончательно:
![]()
Ответ:
![]() - общий интеграл ДУ.
- общий интеграл ДУ.
Задача №3.Найти решение задачи Коши
![]() ,
,![]() .
.
Решение:
ДанноеДУ является линейным
неоднородным ДУпервого
порядка. Решим его методом вариации
произвольной постоянной. Сначала решим
ДУ однородное, т.е.
![]() .
Это всегда ДУ с разделяющимися переменными
.
Это всегда ДУ с разделяющимися переменными![]() - общие решение однородного линейного
ДУ
- общие решение однородного линейного
ДУ
![]() в таком виде будем искать общее решение
неоднородного ДУ, где
в таком виде будем искать общее решение
неоднородного ДУ, где![]() -
неизвестная функция,
-
неизвестная функция,![]() Подставляем
Подставляем![]() и
у в исходноеДУ, будем
иметь;
и
у в исходноеДУ, будем
иметь;
 общее
решение данного ДУ Найдем частное
решение, используя начальные условия
общее
решение данного ДУ Найдем частное
решение, используя начальные условия
![]() .
Итак, задача Коши решена :найдено
частное решение, ДУ, отвечающее начальному
условию
.
Итак, задача Коши решена :найдено
частное решение, ДУ, отвечающее начальному
условию
![]()
![]()
Ответ:
![]()
Задача №4.Найти решение задачи Коши
![]() ,
,![]()
Решение:
Перепишем данноеДУ в
виде
![]() это уравнение Бернулли. Решаем методом
Бернулли:
это уравнение Бернулли. Решаем методом
Бернулли:
![]()

общее решение исходного ДУ.
Решим задачу Коши:

![]()
Ответ:
![]() -
частное решение исходного ДУ,
удовлетворяющего начальному условию
-
частное решение исходного ДУ,
удовлетворяющего начальному условию![]()
Задача №5.
Найти общий итеграл
дифференциального уравнения
![]()
Решение:
Данное ДУ перепишем в
виде
![]()
Проверим, является ли это ДУ
в полных дифференциалах. У нас
![]() ;
;![]() ;
;![]() ;
;![]() ;
так как
;
так как![]() данное ДУ является ДУпервого
порядка, в полных дифференциалах, т.е.
имеет вид
данное ДУ является ДУпервого
порядка, в полных дифференциалах, т.е.
имеет вид
![]() ,откуда
,откуда![]() общий интеграл исходного ДУ. Остается
найти функцию
общий интеграл исходного ДУ. Остается
найти функцию![]() ,
чей полный дифференциал стоит в левой
части уравнения и
,
чей полный дифференциал стоит в левой
части уравнения и![]() ,
,![]() ;
;![]()
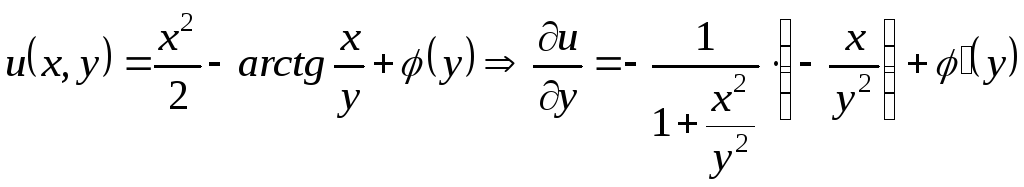 с другой стороны,
с другой стороны,
![]() значит ,
значит ,![]()
![]()
![]() .
Наконец,
.
Наконец,
![]() –
–![]()
![]() и общий интеграл имеет вид
и общий интеграл имеет вид![]() –
–![]()
![]() ,
окончательно
,
окончательно![]() ,
,![]() .
.
Ответ: общий интеграл
![]()
Задача №6.Найти общее решение дифференциального уравнения
![]()
Решение:
Данное ДУ второго порядка не содержит
искомой функций![]() ,
значит, замена переменных такова:
,
значит, замена переменных такова:
![]() ,
откуда уравнение принимает вид:
,
откуда уравнение принимает вид:![]() или
или
![]() ,
т.е. становится ДУ I порядка линейным
неоднородным, решаем его методом
вариации произвольной постоянной.
Сначала рассмотрим однородное уравнение:
,
т.е. становится ДУ I порядка линейным
неоднородным, решаем его методом
вариации произвольной постоянной.
Сначала рассмотрим однородное уравнение:
![]() всегда с разделяющимися переменными:
всегда с разделяющимися переменными:
![]()
![]() ищемобщее решение неоднородного
ДУв таком же виде, только
ищемобщее решение неоднородного
ДУв таком же виде, только
![]() ,
т .е.
,
т .е.
![]() подставляя в неоднородное ДУ, получаем
подставляя в неоднородное ДУ, получаем
 .
Найдем
.
Найдем
![]() ,
выделив сначала целую часть дроби
,
выделив сначала целую часть дроби![]() =
=
![]()
 получим
получим![]()
![]() .Тогда
.Тогда
![]()
Ответ:![]() -
общее решение исходногоДУвторого порядка.
-
общее решение исходногоДУвторого порядка.
Задача №7. Найти общее решение дифференциального уравнения
![]()
Решение:Решаем данное дифференциальное уравнение III порядка линейное неоднородное с постоянными коэффициентами также, как и предыдущее.
Сначала
![]() имеет характеристическое уравнение
имеет характеристическое уравнение![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
умножение наx вызвано
тем, что
,
умножение наx вызвано
тем, что![]() является простым корнем характеристического
уравнения, и число 2 стоит множетелем
при x в
степени показательной функции
является простым корнем характеристического
уравнения, и число 2 стоит множетелем
при x в
степени показательной функции
![]() .
Значит
.
Значит![]()
![]()

![]()

![]() ;
;
![]()
Ответ:
![]()
