
Решение типового варианта индивидуального задания №2
1.Ряды
Задача №1.
Найти сумму ряда![]()
![]() .
.
Решение:
Выведем формулу частичной суммы
рядаSn. Для этого разложим
общий член ряда![]() на сумму простых дробей. Сначала
представим квадратный трехчлен в виде
произведения простых множителей:
на сумму простых дробей. Сначала
представим квадратный трехчлен в виде
произведения простых множителей:![]()

Теперь общий член ряда представим в виде суммы простых дробей с неопределенными коэффициентами
![]() .
.
Найдем числа АиВ, сравнив
коэффициенты при одинаковых степенях
n 
Итак,
![]()
Выведем формулу частичной суммы ряда Sn:

По определению сумма ряда
![]()
![]()
Ответ:
![]() .
.
Задача №2.
Исследовать на сходимость ряд![]()
Решение: Используем признак
Даламбера,вычисляя![]() у нас
у нас![]() ,
,![]() .
Получим
.
Получим

ряд сходится.
Задача №3.
Исследовать на сходимость ряд
![]()
Решение: Применим радикальный
признак Коши, вычисляя![]() у нас:
у нас: ряд сходится.
ряд сходится.
Задача №4.
Исследовать на сходимость ряд
![]()
Решение: Применим интегральный признак Коши, исследуя на сходимость несобственный интегралпервогорода:
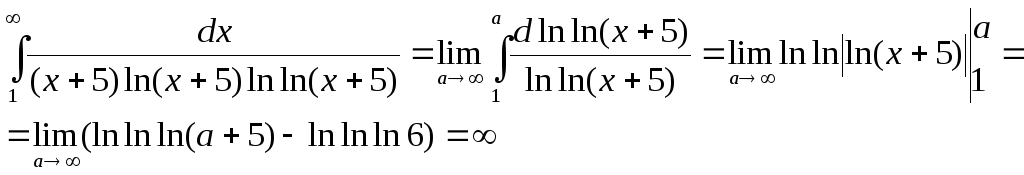
Следовательно, интеграл расходится, а значит, расходится и данный ряд.
Задача №5.
Исследовать на сходимость ряд![]()
Решение: К данному знакочередующемуся ряду применим признак Лейбница.
1) Докажем, что последовательность
![]() убывающая. Начнем с очевидного неравенства:
убывающая. Начнем с очевидного неравенства: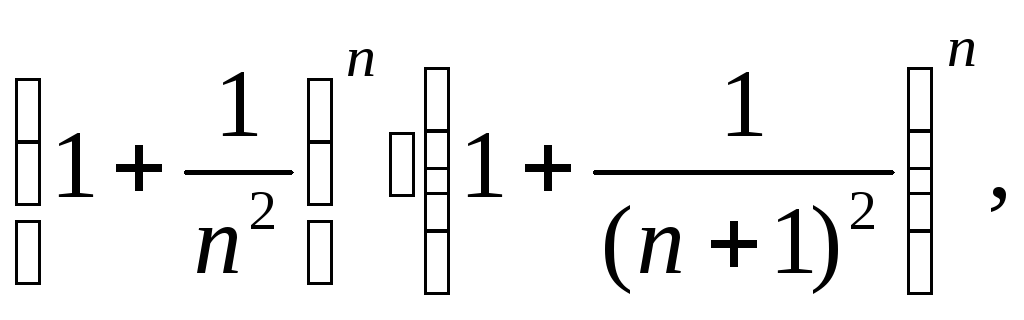 если мы умножим правую часть неравенства
на выражение, большее 1, то только его
«усилим», т.е. очевидно, что
если мы умножим правую часть неравенства
на выражение, большее 1, то только его
«усилим», т.е. очевидно, что
 .
Что и требовалось
доказать.
.
Что и требовалось
доказать.
2) Вычислим
![]() Для этого, используя правило Лопиталя,найдем предел функции.Таким образом, признак
Лейбница выполнен, значит знакочередующийся
ряд сходится. Уточним характер сходимости
ряда. Ряд из абсолютных величин исходного
можно сравнить с расходящимся
гармоническим рядом
Для этого, используя правило Лопиталя,найдем предел функции.Таким образом, признак
Лейбница выполнен, значит знакочередующийся
ряд сходится. Уточним характер сходимости
ряда. Ряд из абсолютных величин исходного
можно сравнить с расходящимся
гармоническим рядом![]() .
.
 ряды ведут себяодинаково
т.е. данный ряд как игармонический, расходится, следовательно,
исходный знакочередующийся ряд сходится
условно.
ряды ведут себяодинаково
т.е. данный ряд как игармонический, расходится, следовательно,
исходный знакочередующийся ряд сходится
условно.
Задача №6.Найти
область сходимости ряда ![]()
Решение:Применим радикальный признак Коши при нахождение области сходимости ряда.

Исследуем ряд на границе области
сходимости, т.е. при
![]() и при
и при![]() .
При
.
При![]() получим числовой ряд
получим числовой ряд![]() применим к данному ряду признак
Даламбера, получим:
применим к данному ряду признак
Даламбера, получим:

 ряд сходится. При
ряд сходится. При![]() получим ряд
получим ряд![]() знакочередующийся вида
знакочередующийся вида![]() Применяя к нему признак Лейбница,найдем
Применяя к нему признак Лейбница,найдем![]() ,
получим:
,
получим:
![]()
 ряд сходится.
ряд сходится.
Ответ:Область сходимости исходного
ряда:![]()
Задача №7.
Найти область сходимости ряда![]()
Решение: Применим признак Даламбера

При х = 2
![]() горманический
ряд сходится. (2n-1) –
нечетно при любомnт.е.
(-1)2n-1=
- 1.
горманический
ряд сходится. (2n-1) –
нечетно при любомnт.е.
(-1)2n-1=
- 1.
Значит х = 2![]() области сходимости. При
х = 8
области сходимости. При
х = 8 ![]() - знакочередующийся ряд, по признаку.
Лейбница: 1)
- знакочередующийся ряд, по признаку.
Лейбница: 1)![]() - убывающая последовательность.
2)
- убывающая последовательность.
2)![]() .
Итак, ряд
.
Итак, ряд![]() сходится условно, т.к. ряд из абсолютных
величин исходного является гармоническим,
следовательно, расходящимся рядом;
значит, х = 8
сходится условно, т.к. ряд из абсолютных
величин исходного является гармоническим,
следовательно, расходящимся рядом;
значит, х = 8![]() области сходимости ряда.
области сходимости ряда.
Ответ: 2 < х ≤ 8.
Задача №8.
Найти интервал сходимости степенного
ряда
![]() .
.
Решение: Применим
признак Даламбера
![]()
![]()
![]()
![]()
![]() .
.
Ответ:
![]() .
.
Задача №9.
Вычислить с помощью рядов интеграл
![]() .
.
Решение: Применим
формулу разложения функции в ряд
![]()
![]()
![]()
2. Теория вероятностей и математическая статистика
Задача 1.Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходитN; б) произведение числа очков не превосходитN; в) произведение числа очков делится наN.
Дано: N=6
Найти: P1-? P2-? P3-?
Решение. Рассмотримвсе возможные варианты:
|
i:j |
i:j |
i:j |
i:j |
i:j |
i:j |
|
1:1 |
2:1 |
3:1 |
4:1 |
5:1 |
6:1 |
|
1:2 |
2:2 |
3:2 |
4:2 |
5:2 |
6:2 |
|
1:3 |
2:3 |
3:3 |
4:3 |
5:3 |
6:3 |
|
1:4 |
2:4 |
3:4 |
4:4 |
5:4 |
6:4 |
|
1:5 |
2:5 |
3:5 |
4:5 |
5:5 |
6:5 |
|
1:6 |
2:6 |
3:6 |
4:6 |
5:6 |
6:6 |
Используем классическую формулу![]() ,
гдеn=36
,
гдеn=36
а) i+j≤N. В первом столбце сумма числа очков во всех строках меньше 6, следовательно,m1=5, во втором столбце такжеm2=4, в третьем –m3=3, в четвертомm4=2, в пятом –m5=1, в шестом –m6=0. В итоге, суммируя, получаемm=15;Тогда
![]()
б) i∙j≤N. Поступая аналогично предыдущему случаю, подсчитываем произведение числа очков по столбцам, удовлетворяющих заданному условию. В итоге, получаемm=14;
![]()
в) i∙j![]() N.
Подсчитав число случаев, удовлетворяющих
данному условию, получаемm=5;
N.
Подсчитав число случаев, удовлетворяющих
данному условию, получаемm=5;
![]()
Ответ: P1=0,42; P2=0,39; P3=0,42.
Задача 2.Имеются
изделия 4 –х сортов, причем число изделийi– го сорта равноni,i – 1,2,3,4. Для
контроля наудачу берутсяmизделий. Определить вероятность того,
что среди нихm1
первосортных,m2,
m3 и m4,второго, третьего и четвертого сорта
соответственно.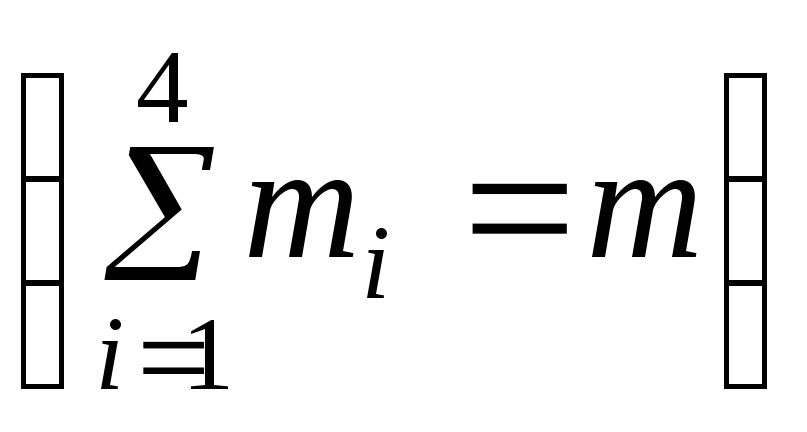 .
.
Дано: n1=3, n2=2, n3=3, n4=1, m1=2, m2=2, m3=2, m4=0.
Найти: P-?
Решение.ОбозначимА– все множество изделий, подвергающихся контролю,В– множество изделий, взятых на контроль изА.Подсчитаем число способов, которыми можно выбрать множествоВизА:
![]() .
.
Число способов, с помощью которых
выбирают m1
изn1,m2 изn2и т.д.,
равно![]() ,
т.е.
,
т.е.
![]()
Используя классическую формулу, получаем
![]() .
.
Ответ: 0,11.
Задача 3. Средиnлотерейных билетовk– выигрышных. Наудачу взялиmбилетов. Определить вероятность того, что среди нихlвыигрышных.
Дано: n=9, l=3, m=5, k=4.
Найти: P-?
Решение. По
классический формуле![]() ,
получаем
,
получаем
![]() ,
,
где
![]() - число способов, с помощью которых изnлотерейных билетов
взялиm билетов,
- число способов, с помощью которых изnлотерейных билетов
взялиm билетов,![]() - число способов, с помощью которых изmвзятых билетов взялиlвыигрышных.
- число способов, с помощью которых изmвзятых билетов взялиlвыигрышных.
Ответ:0,3.
Задача 4.В круге радиуса![]() наудачу появляется точка. Определить
вероятность того, что она попадает в
одну из двух не пересекающихся фигур,
площади которых равны
наудачу появляется точка. Определить
вероятность того, что она попадает в
одну из двух не пересекающихся фигур,
площади которых равны![]() и
и![]() .
.
Дано:
![]() ,
,![]() ,
,![]() .
.
Найти:
![]()

Рисунок 10– Геометрическая интерпретация задачи
Решение. По формуле геометрической вероятности (рис.10) имеем
![]() .
.
Отсюда получим
![]() .
.
Ответ:![]() .
.
Задача 5.В двух
партиях![]() и
и![]() %
доброкачественных изделий соответственно.
Наудачу выбирают по одному изделию из
каждой партии. Какова вероятность
обнаружить среди них:
%
доброкачественных изделий соответственно.
Наудачу выбирают по одному изделию из
каждой партии. Какова вероятность
обнаружить среди них:
 - хотя бы одно бракованное;
- хотя бы одно бракованное; -
два бракованных;
-
два бракованных; - одно доброкачественное и одно
бракованное?
- одно доброкачественное и одно
бракованное?
Дано:
![]() ,
,![]() .
.
Найти:
![]()
![]()
![]()
Решение. Введем обозначения:
пусть событие
![]() -
выбор доброкачественного изделия из
первой партии, событие
-
выбор доброкачественного изделия из
первой партии, событие![]() -выбор
доброкачественного изделия из второй
партии,
-выбор
доброкачественного изделия из второй
партии,
событие ![]() -
выбор бракованного изделия из первой
партии,
-
выбор бракованного изделия из первой
партии,
событие ![]() -
выбор бракованного изделия из второй
партии.
-
выбор бракованного изделия из второй
партии.
Тогда
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Искомое событие В - хотя бы одно бракованное, равно
![]() ,
,
где все события
![]() несовместные.
несовместные.
Вероятность выбора хотя бы одного бракованного изделия
![]() или
или
![]()
Искомое событие - два бракованных, тогда
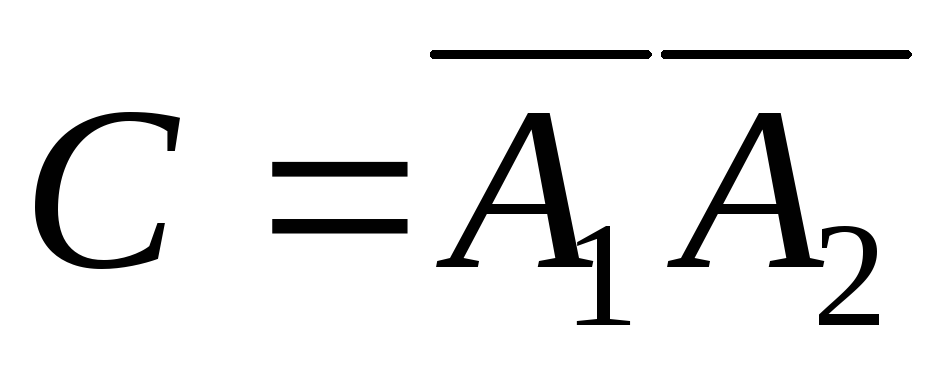 ,
где
,
где  - независимые события. Вероятность
выбора двух бракованных изделий равна
- независимые события. Вероятность
выбора двух бракованных изделий равна
![]() или
или![]() .
.
Искомое событие - одно доброкачественное и одно бракованное:
![]() .
.
Вероятность выбора одно доброкачественное и одно бракованное изделий
![]() или
или
![]() .
.
Ответ:![]() ,
,![]() ,
,![]() .
.
Задача 6.Вероятность
того, что цель будет поражена при одном
выстреле первым стрелком равна ![]() ,
вторым -
,
вторым -![]() .
Первый сделал
.
Первый сделал![]() (событиеА), второй
(событиеА), второй![]() выстрелов (событиеВ). Определить
вероятность того, что цель не поражена.
выстрелов (событиеВ). Определить
вероятность того, что цель не поражена.
Дано:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Найти
![]()
Решение. Определим вероятность
промаха для первого и второго стрелков
при одном выстреле, соответственно, по
формуле![]() .
.
![]() .
.
![]() .
.
Для вычисления искомой вероятности
используем формулу умножения вероятностей
для независимых событий
![]() .
.
Вероятность промаха для первого стрелка
при
![]() выстрелах равна
выстрелах равна![]() ,
для второго -
,
для второго -![]() .
.
![]() .
.
Ответ:![]() .
.
Задача 7.Вероятность выигрыша в лотерею на один билет равнаp. Купленоnбилетов. Найти наивероятнейшее число выигравших билетов и соответствующую вероятность. (См. п. 1.6 и исходные данные).
Дано:
![]()
Найти:
![]()
Решение. Из теории известно, что
![]() ,
если
,
если
![]() целое число, тоk0
имеет два значения, если дробное
целое число, тоk0
имеет два значения, если дробное
![]() (целой части).
(целой части).
В нашем случае наивероятнейшее число успехов
![]() .
.
Искомую вероятность подсчитаем по формуле Бернулли:
![]() .
.
![]() =
=
![]() .
.
Ответ:
![]() .
.
