
Умножение5
.doc
Для получения результата ребенок может воспользоваться любой из упомянутых выше моделей.
При больших значениях делимого и делителя этот прием неудобен. Например: 72 горшка с цветами расставили на 8 окон. Сколько горшков на каждом окне?
Находить результат, используя предметную модель в этом случае неудобно.
2. Прием, связанный с правилом взаимосвязи компонентов умножения и деления
В этом случае ребенок ориентируется на запоминание взаимосвязанной тройки случаев, например:
7-9 = 63 63:7 = 9 63:9 = 7
Если ребенку удается хорошо запомнить один из этих случаев (обычно опорный — это случай умножения) или он может получить его с помощью любого из приемов запоминания таблицы умножения, то используя правило «если произведение разделить на один из множителей, то получится второй множитель», легко получить второй и третий табличные случаи.
Особые случаи умножения и деления
1. Умножение и деление с 0 и 1.
2. Внетабличное умножение и деление в пределах 100.
3. Деление с остатком.
4. Приемы устных вычислений умножения и деления трехзначных и многозначных чисел.
1. Умножение и деление с О и 1
Случаи умножения и деления с 0 и 1 считаются особыми и рассматриваются отдельно от табличных случаев умножения и деления, поскольку они не могут быть объяснены с общих позиций смысла действий умножения и деления. Для обоснования математического смысла этих случаев в определении действия умножения оговорены два дополнения, определяющие способ получения результата в этих случаях.
По определению умножение целых неотрицательных (натуральных) чисел — это действие, выполняющееся по следующим правилам:
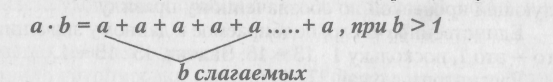
а • 1 = а, при Ь = 1 а-0 = 0,приЪ = 0
Поскольку фраза: «повторяем слагаемые 1 раз» или «повторяем слагаемые 0 раз» не имеет смысла, на общее определение в этом случае не ссылаются, а просто вводят эти случаи по соглашению т. е. сообщают детям, что умножая любое число на 1 получаем в произведении это же число; а умножая любое число на 0, получаем в произведении 0.
В общем виде эти правила оформляются в буквенном выражении:
| ах1 = а | | ах0 = 0 |
Соответствующие правила предлагаются детям для запоминания:
При умножении любого числа на 1 получается то число, которое умножали.
При умножении любого числа на нуль получается нуль.
Аналогичным образом вводится правило: На нуль делить нельзя!
В отличие от этих правил, способы деления числа на само себя с получением числа 1 в результате, а также способы умножения числа 1 на любое число и способы умножения числа 0 на любое число возможно объяснить ученику начальной школы, используя имеющиеся у него знания.
Например, для объяснения случая 1 • 7 обратимся к смыслу действия умножения как суммирования одинаковых слагаемых. В данной записи первый множитель показывает, какое число суммируем, а второй множитель сколько раз, таким образом:
1-7 = 1 + 1 + 1 + 1 + 1 + 1 + 1 = 7
Для объяснения случая 0 • 5 воспользуемся тем же приемом:
0-5=0+0+0+0+0=0
Для объяснения случаев вида а : а = 1 (если а Ф 0), а : 1 = а, О : а = 0 следует обратиться к правилу взаимосвязи компонентов умножения и деления.
Например, рассмотрим случай 13 : 13 = ...
Для получения значения частного воспользуемся правилом: «если значение частного умножить на делитель, то получим делимое». Делитель — число 13, найдем частное методом подбора с последующей проверкой по обозначенному правилу.
Единственное число, подбираемое к данному значению частного — это 1, поскольку 1 • 13 = 13. Значит, 13 : 13 = 1.
Рассмотрим случай 27 : 1 =*...
Для получения значения частного воспользуемся правилом: «если значение частного умножить на делитель, то получим делимое». Делитель — число 1, найдем частное методом подбора с последующей проверкой по обозначенному правилу.
Единственное число, подбираемое к данному значению частного — это 27, поскольку 27 • 1 = 27. Значит, 27 : 1 = 27.
Рассмотрим случай 0:8 = ...
Для получения значения частного воспользуемся правилом: «если значение частного умножить на делитель, то получим делимое». Делитель — число 8, найдем частное методом подбора с последующей проверкой по обозначенному правилу.
Единственное число, подбираемое к данному значению частного — это 0, поскольку 0-8 = 0. Значит, 0:8 = 0.
В общем виде эти закономерности оформляются в буквенном виде:
а:а = 1 а:1=а 0:а = 0
и в виде словесного правила:
При делении числа на то же самое число получается 1.
При делении числа на 1 получается то же самое число.
При делении нуля на любое другое число получается 0.
2. Внетабличное умножение и деление в пределах 100
К внетабличным случаям умножения и деления в пределах 100 относят случаи умножения двузначного числа на однозначное (20 • 3, 18 • 3), а также случаи деления двузначного числа на однозначное, не входящие в число табличных (80 : 4, 96 : 6) и случаи деления двузначного числа на двузначное в пределах 100 (80 : 40, 96 : 16). Эти случаи рассматриваются как случаи устных вычислений, и предполагается, что ребенок выполняет их без обращения к письменным алгоритмам вычислений, а лишь используя известные ему правила и законы арифметических действий и знание табличного умножения и деления.
Используемые математические законы и правила
Для подготовки к изучению внетабличного умножения и деления необходимо рассмотреть следующие правила арифметических действий:
1) правило умножения суммы на число и правило умножения числа на сумму;
2) правило деления суммы на число;
3) правило группировки множителей (сочетательное свойство умножения).
Рассмотрим каждое из этих правил и обоснуем их использование при устных внетабличных вычислениях.
Правило умножения суммы на число и правило умножения числа на сумму
Эти два правила являются двумя вариантами раскрытия смысла распределительного свойства умножения относительно сложения. В буквенном виде эти варианты могут быть записаны следующим образом:
![]()
Реально знакомство детей с этими двумя вариантами одного и того же правила разведено во времени почти на целый год: первое правило лежит в основе обучения детей умножению двузначных чисел на однозначные в теме «Внетабличное умножение и деление» в 3 классе, а второе правило лежит в основе способа действия при умножении двузначного числа на двузначное при умножении в столбик в 4 классе.
В основе разъяснения правила умножения суммы на число лежит опора на знание конкретного смысла действия умножения.
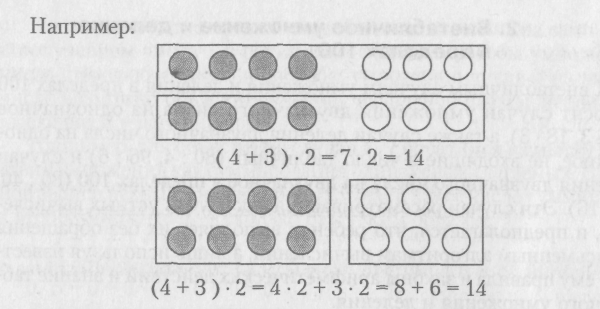
Рассматривая два способа вычисления результатов с опорой на анализ рисунка, дети убеждаются в том, что результат при обоих способах вычислений одинаков.
Следует отметить, что первый способ вычислений не требует специальных объяснений и введения нового правила, поскольку он подчиняется общим требованиям к порядку выполнения действий в выражениях со скобками: действия в скобках выполняются первыми.
Особо следует оговорить второй способ, поскольку при таких вычислениях фактически нарушается установка на выполнение действия в скобках первым. Именно поэтому при знакомстве детей с этим правилом в 3 классе снова возвращаются к предметным картинкам, позволяющим получить результаты действий пересчетом. В данном случае пересчет фигурок является тем единственным аргументом, который учитель может привести в подкрепление правомочности такого нарушения устоявшегося правила (действие в скобках выполняется первым).
Введение правила таким образом является нестрогим, эмпирическим (т. е. опирающимся на непосредственный практический опыт). Более общие способы доказательства этого закона требуют привлечения сложного математического аппарата и нецелесообразны в начальной школе.
