7. Формула Байеса, определение и свойства гипотез.

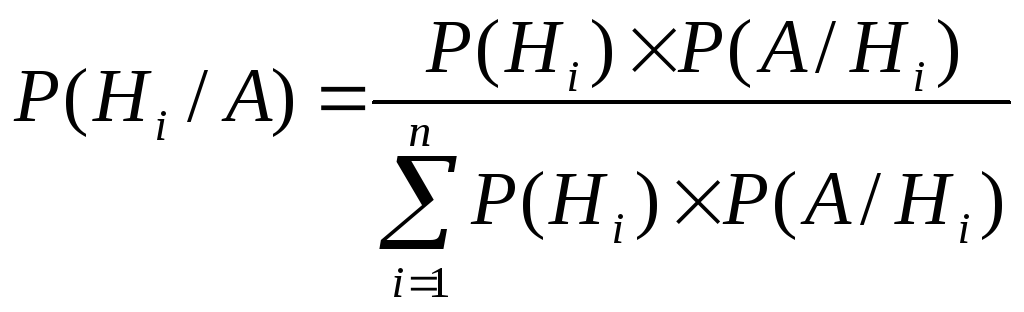
Т. Вероятность гипотезы после испытания равна произведению вероятности гипотезы на соответствующую ей условную вероятность события, деленному на полную вероятность этого события

Гипотезы – несовместные события, образующие полную группу, с одним из которых может наступить или не наступить событие А. каждая гипотеза имеет свою вероятность, и в сумме должны давать 1(полная группа же!)

8. Повторные испытания, формула Бернулли, формула Пуассона.

Т. Если вероятность наступления события А в каждом испытании постоянна, то вероятность того, что событие А наступит m раз в n независимых испытаниях, равна:

, где -формула Бернулли.

Позволяет находить вероятность появления события А при независимых испытаниях.

Т. Если вероятность р наступления события А в каждом испытании постоянна, но мал, число независимых испытания n достаточно велико, но значение произведения остается небольшим (не больше 10), то вероятность того, что в этих испытаниях событие А наступит m раз

, где - Формула Пуассона

Применяется при малых р и np, так, что фомула Лаплассса будет недостаточно точной

9. Комбинаторика. Определение и формулы перестановки и сочетаний. Примеры вычислений.

Перестановкой называется всякое упорядоченное конечное множество, образованное из всех его элементов.

Ex: Требуется рассадить 6 зрителей в ряду из 6 мест.

P_n=6!=1*2*3*4*5*6=720

Сочетанием из n элементов, взятых по m элементов, называется всякая часть множества, содержащая m элементов

Ех: Определить число возможностей выбрать 2 любых билета в лотерее, в которой разыгрывается 100 билетов.

10. Повторные испытания. Локальная, интегральная теорема Лапласса.

Локальная.

Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р_m,n того, что событие А появится в n испытаниях ровно m раз, приближенно (тем точнее, чем больше n) значению функции

, при - табличное значение.

Т.о. приближенно вероятность того, что событие А появится в n испытаниях ровно m раз,

, где .

Применяется при больших значения n, где пользоваться формулой Бернулли затруднительно.

Интегральная.

Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то приближенная вероятность того, что событие А появится в испытаниях от m₁ до m₂ раз,

, где

- табличное значение

Т.о. приблеженно вероятность того, что событие А появится в испытаниях от m₁ до m₂ раз

, где

Применяется при вычислении вероятности того, что событие А появится в n испытаниях не менее m₁ и не более m₂ раз.