
- •4. Автоматизация фотограмметрических измерений
- •Корреляционный метод измерений соответственных точек на паре снимков
- •Измерение соответственных точек по методу наименьших квадратов
- •Проблемы автоматического стереоотождествления одноименных точек
- •Отождествление соответственных точек по методу наименьших квадратов с учетом геометрических и фотометрических искажений снимков
- •Отождествление соответственных точек по методу наименьших квадратов в пространстве объекта
- •Вычисление градиента изображения
- •Методы, позволяющие сузить область поиска соответственных точек на смежных снимках
- •Использование априорной информации о параметрах съемки
- •Построение пирамиды изображений
- •Поиск точек на стереопаре снимков идеального случая съемки
- •Использование базисных линий на нескольких перекрывающихся снимках
- •Сужение области поиска вдоль базисных линий
- •4.8 Построение цифровой модели поверхности.
- •Оператор Форстнера (Forstner)
- •Оператор Моравика (Moravec)
- •Оператор Дрешлера (Dreschler)
- •Оператор Марра (LoG - Лапласиан Гауссиана)
- •Sift (масштабно инвариантное преобразование)
- •Автоматизированные методы монокулярных измерений
- •Вычисление центра тяжести фигуры
- •Вычисление центра на основе уравнения фигуры
- •Корреляционный метод
- •4.11 Применение методов автоматизации измерений в фотограмметрии
Отождествление соответственных точек по методу наименьших квадратов с учетом геометрических и фотометрических искажений снимков
До сих пор (см. параграф 4.2) мы предполагали, что параллаксы являются постоянными величинами в пределах фрагментов изображений. Однако на практике это не так. Вследствие геометрических несоответствий (искажений) двух фрагментов изображений, вызванных влиянием разности высот фотографирования, углов наклона снимков и рельефа местности параллаксы в каждом пикселе будут свои (см. параграф 4.3). Кроме того, снимки имеют фотометрические несоответствия.
Геометрические искажения двух фрагментов изображений можно описать с помощью аффинных, конформных, проективных или перспективных преобразований. Для снимков, полученных по законам центрального проектирования наилучшим образом подходят естественно перспективные преобразования (уравнения коллинеарности). Ниже будет рассмотрен этот вариант.
Как показывает практика, для небольших фрагментов изображений геометрические искажения с достаточной степенью точности могут быть описаны с помощью аффинных преобразований. Рассмотрим этот вариант учета разности геометрических искажений двух фрагментов изображений:
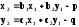 , (
4.10)
, (
4.10)
тогда исходное уравнение (4.7) примет вид:
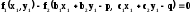 (4.11)
(4.11)
В этом уравнении неизвестными являются параллаксы (p,q) и коэффициенты аффинных преобразований (b1,b2,c1,c2). Тогда соответствующее уравнение поправок можно записать так:
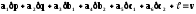 (4.12)
(4.12)
Частные производные имеют вид:
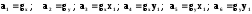 (4.13)
(4.13)
свободный член ℓ вычисляется по формуле (4.12), подставляя в нее приближенные значения неизвестных.
Неизвестные параллаксы и коэффициенты аффинных преобразований находят по способу наименьших квадратов, методом последовательных приближений. Причем после каждого приближения, уточнив значения неизвестных параллаксов и коэффициентов аффинных преобразований, следует сформировать новый фрагмент изображения (матрицу поиска) на правом снимке (рис. 4.10).
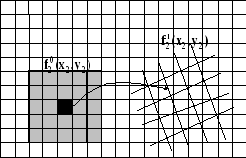
Рис. 4.10
При этом коордиаты пикселей матрицы поиска вычисляются по формулам (4.10), а соответствующие плотности – по исходному снимку методом двойного линейного интерполирования. Здесь следует учитывать то обстоятельство, что в результате аффинных преобразований каждый пиксель матрицы поиска может увеличиться по площади и для получения его плотности следует использовать все пиксели исходного снимка, которые он накрывает, а не только 4 соседних пикселя. Полученные таким образом плотности изображения участвуют в формировании уравнений (4.12).
Фотометрические различия между двумя фрагментами изображений могут быть описаны с помощью, например, линейных преобразований. Тогда уравнение (4.11) можно записать как:
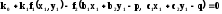 , (
4.14)
, (
4.14)
а соответствующее уравнение поправок:
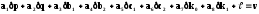 (4.15)
(4.15)
Частные производные а1-а6 вычисляются по (4.13), а остальные по формулам:
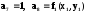 (4.16)
(4.16)
Таким образом, на основе уравнения (4.15) находят по методу наименьших квадратов продольный и поперечный параллаксы для данной точки с учетом геометрических и фотометрических различий между фрагментами изображений двух снимков.
Следует отметить, что если обрабатываются цветные снимки, то коэффициенты фотометрических преобразований k0 и k1 находят для каждого канала (красный, синий, зеленый). Для этого для каждого пикселя составляют три уравнения ( 4.15).
Как показывают экспериментальные исследования, применение цветных изображений приводит к незначительному повышению точности отождествления одноименных точек по сравнению с черно-белыми изображениями или по сравнению с отождествлением по одному красному каналу. Поэтому иногда цветные изображения переводят в черно-белые и затем выполняют фотограмметрическую обработку, что приводит к выигрышу по времени обработки.
Метод наименьших квадратов позволяет найти параллаксы с точностью до 0.01 пикселя. Однако этот метод имеет и существенный недостаток – необходимость знания начальных приближений параллаксов с достаточной точностью (1-2 пикселя) и выполнения большого числа приближений, что может замедлить процесс вычислений.
Несколько слов о величине фрагментов изображений. Очевидно, что она влияет на точность отождествления точек. Чем меньше размеры фрагментов изображений, тем меньше число избыточных измерений, а как следствие понижается точность и надежность отождествления. С другой стороны при увеличении размеров фрагментов изображений увеличивается вероятность ложных отождествлений. Поэтому желательно иметь возможность менять размеры фрагментов в зависимости от качества исходных снимков. Если снимки хорошего фотографического качества с высоким контрастом и с изображением большого количества деталей местности отождествление можно начать с применения фрагментов размером 5х5, 7х7 или 9х9. Для снимков с повышенным уровнем фотометрического шума и низкой текстурой рекомендуется применять фрагменты размером 21х21 и даже более.
