7.5 Точность наземной стереофотограмметрической съемки.

В большинстве случаев при выполнении наземной стереофотограмметрической съемки используют нормальный случай съемки. Формулы связи координат точек объекта и координат их изображений на снимках стереопары нормального случая съемки в базисной системе координат можно получить из известных формул прямой фотограмметрической засечки 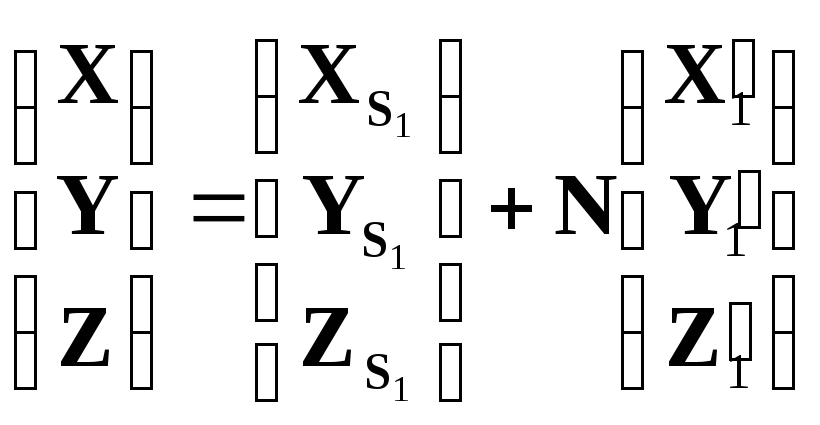(7.8)

, ( 7.8)

в которых:

_,

_.

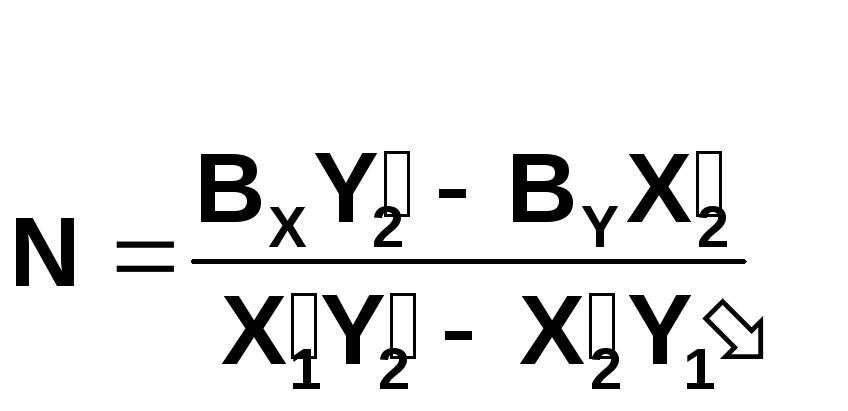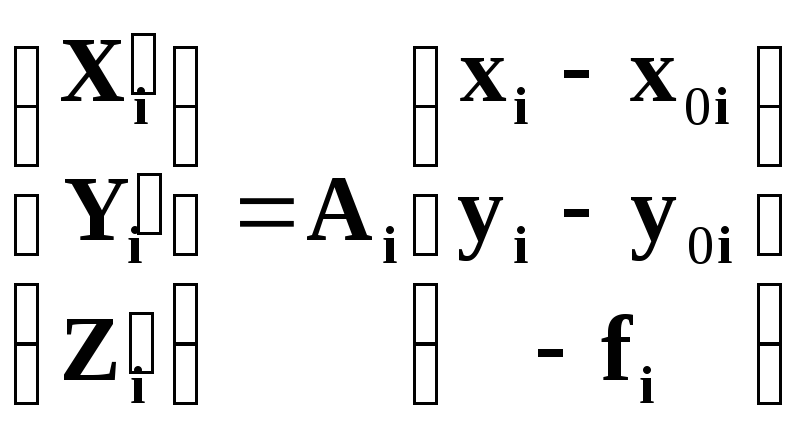В нормальном случае съемки в базисной системе координат угловые элементы внешнего ориентирования ₁ = ₁ = ₂ = ₂ = 0, ₁ = ₂ = 90⁰, _, B_Y=O.

Будем считать, что f₁ = f₂ = f, а x_0i = y_0i= 0.

В этом случае матрицы преобразования координат

.

Следовательно

_,

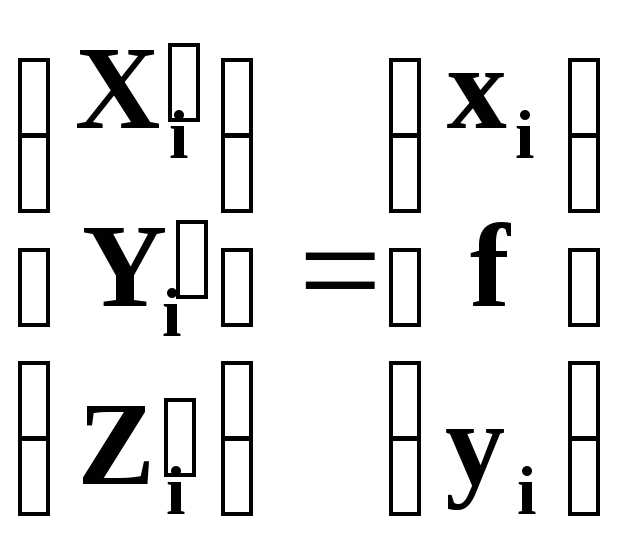а _.

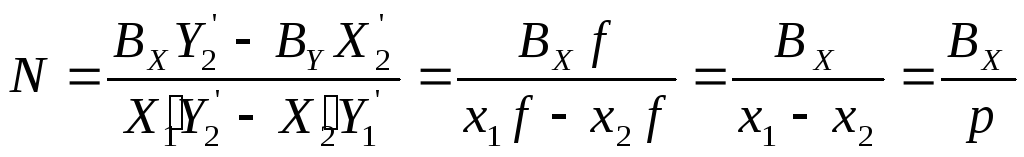В этом случае формулы (7.8) имеют вид

(7.9)

Из второго уравнения формул (7.9) следует, что

.

Заменив в первом и третьем уравнении формул (7.9) выражение на получим

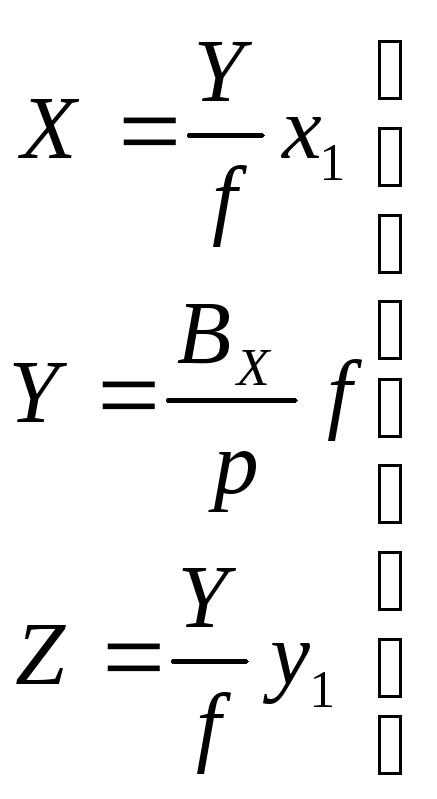. (7.10)

Продифференцировав уравнения (7.10) по переменным x, y и p и перейдя к средним квадратическим погрешностям, заменив значение p на b, получим формулы (7.11) предрасчета точности определения координат точек объекта по стереопаре снимков нормального случая съемки.

(7.11)

В формулах (7.11):

m_x, m_y ,m_p - средние квадратические ошибки измерения координат и продольных параллаксов изображений точек на стереопаре снимков;

Y – отстояние от точки фотографирования до объекта съемки (значение координаты Y в базисной системе координат );

b - базис фотографирования в масштабе снимка вычисляется по формуле

, (7.12)

в которой l_x - размер кадра по оси х, а Р – продольное перекрытие снимков стереопары, выраженное в %.

В качестве примера рассчитаем точность определения координат точек объекта по стереопаре нормального случая съемки цифровой фотокамерой Kodak DCS Pro14 при расстоянии от объекта до точек фотографирования равном 400 метров. При этом будем считать, что продольное перекрытие снимков равно 60 %, а средние квадратические погрешности измерения координат и продольного параллакса на стереопаре снимков равны 0,5 пикселя.

При съемке с горизонтальным расположением кадра для камеры Kodak с f = 4000pix и l_x = 4500pix значение базиса фотографирования в масштабе снимка вычисленное по формуле (7.12) b = 1800 pix, а значения средних квадратических погрешностей определения координат точек объекта равны:

При съемке с вертикальным расположением кадра l_x = 3000pix, значение базиса фотографирования в масштабе снимка b = 1200 pix, а значения средних квадратических погрешностей определения координат точек объекта равны:

Длина базиса фотографирования В на местности (расстояние между точками фотографирования) вычисляется по формуле:

B = Yb/ f.

Для нашего примера значение базиса фотографирования при съемке с горизонтальным расположением кадра будут равны B = 180m. и B = 120m при съемке с вертикальным расположением кадра.

Формулы (7.11) можно использовать и для расчета точности определения координат точек объекта при использовании при съемке объекта равноотклоненного и равнонаклонного случаев съемки. При использовании равнонаклонного случая съемки при вычислении точности определения координат точек объекта значение Y умножается на величину 1/cos, а при использовании равноотклоненного случая съемки значение b умножается на величину сos .

Предрасчет точности определения координат точек объекта по стереопаре снимков позволяет установить требования к точности определения координат и высот опорных точек, определяемых геодезическими методами. Средние квадратические погрешности определения координат и высот опорных точек должны быть не более 1/3 от значений средних квадратических погрешностей определения координат и высот точек объекта по стереопаре снимков.